二叉树之（最近）公共祖先

思路：

考虑问题一个简单的问题：如何寻找一个或多个元素:
Eg: 寻找值为 val1 或 val2 的节点

非常简单：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
// 定义：在以 root 为根的二叉树中寻找值为 val1 或 val2 的节点
TreeNode find(TreeNode root, int val1, int val2) {
    // base case
    if (root == null) {
        return null;
    }
    // 前序位置，看看 root 是不是目标值
    if (root.val == val1 || root.val == val2) {
        return root;
    }
    // 去左右子树寻找
    TreeNode left = find(root.left, val1, val2);
    TreeNode right = find(root.right, val1, val2);
    // 后序位置，已经知道左右子树是否存在目标值

    return left != null ? left : right;
}

236. 二叉树的最近公共祖先

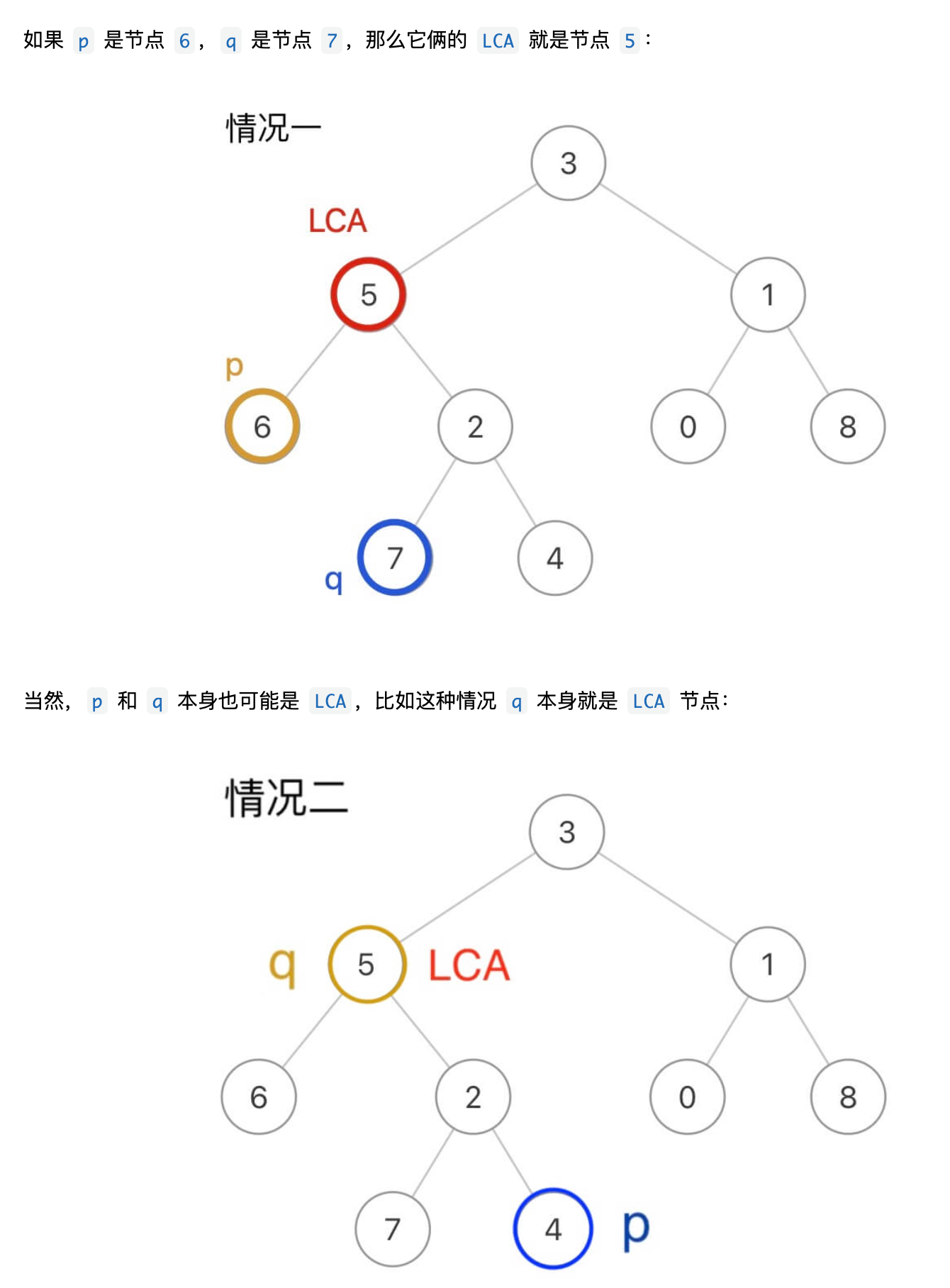
LC236公共祖先

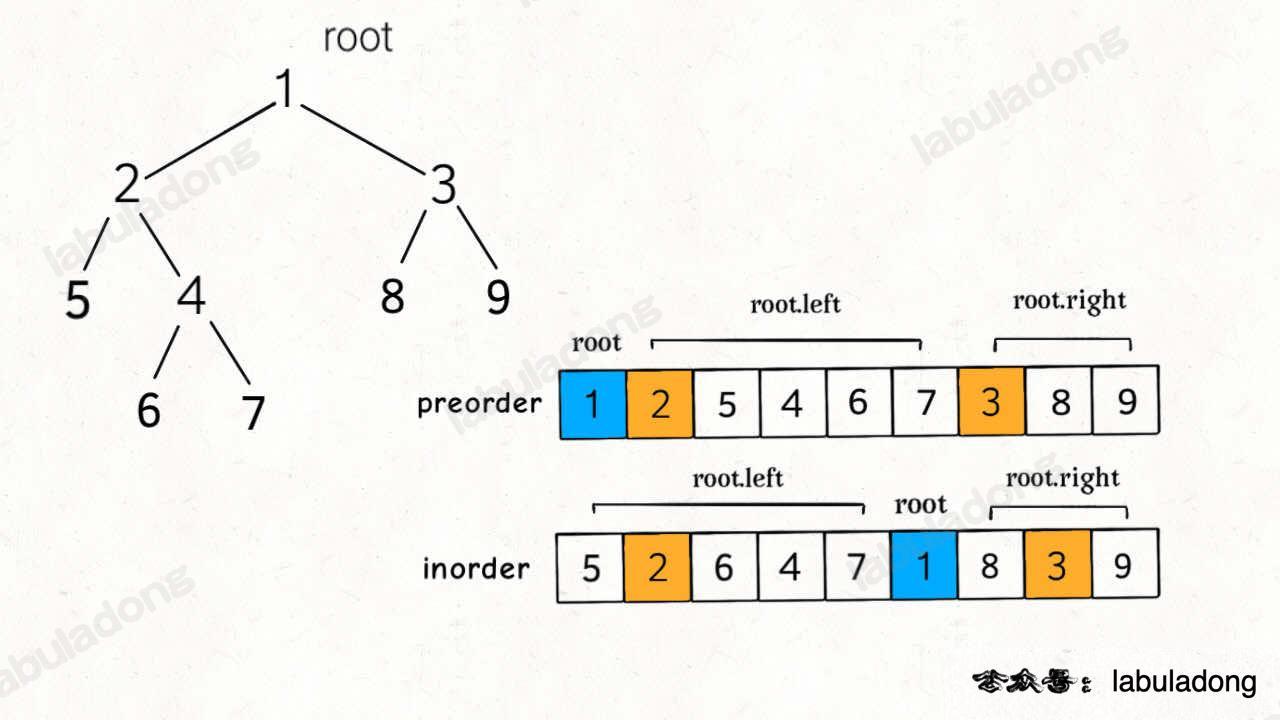
那么对于寻找LCA来说，其实就是找 在一个子树下面是否能够同时找到p和q，寻找最近的公共节点就是寻找最深的公共节点，因此要选择后序遍历

那么我们就会得出：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
    // 通过这个function 来找到子树里是否含有 p 和 q：
    return findTargeValues(root, p, q);
}

private TreeNode findTargeValues(TreeNode root, TreeNode p, TreeNode q) {
    if (root == null) return null;

    // 前序遍历位置，解决情况二：一旦发现有值等于target值，那么它本身就作为最近的祖先；
    // 因为题目说了 p 和 q 一定存在于二叉树中(这点很重要），
    // 所以即便我们遇到 q 就直接返回，根本没遍历到 p，也依然可以断定 p 在 q 底下，q 就是 LCA 节点。
    if (root.val == p.val || root.val == q.val) {
        return root;
    }

    TreeNode leftValue = findTargeValues(root.left, p, q);
    TreeNode rightValue = findTargeValues(root.right, p, q);

    // 后序遍历位置，如果leftValue != null 证明左子树中含有target值，rightValue同理
    // 若同时满足，那么当前root就为最近的公共祖先。
    if (leftValue != null && rightValue != null) {
        return root;
    }

    // 返回不是null的那个或者全是null的，不是null的优先返回。
    return leftValue == null ? rightValue : leftValue;
}

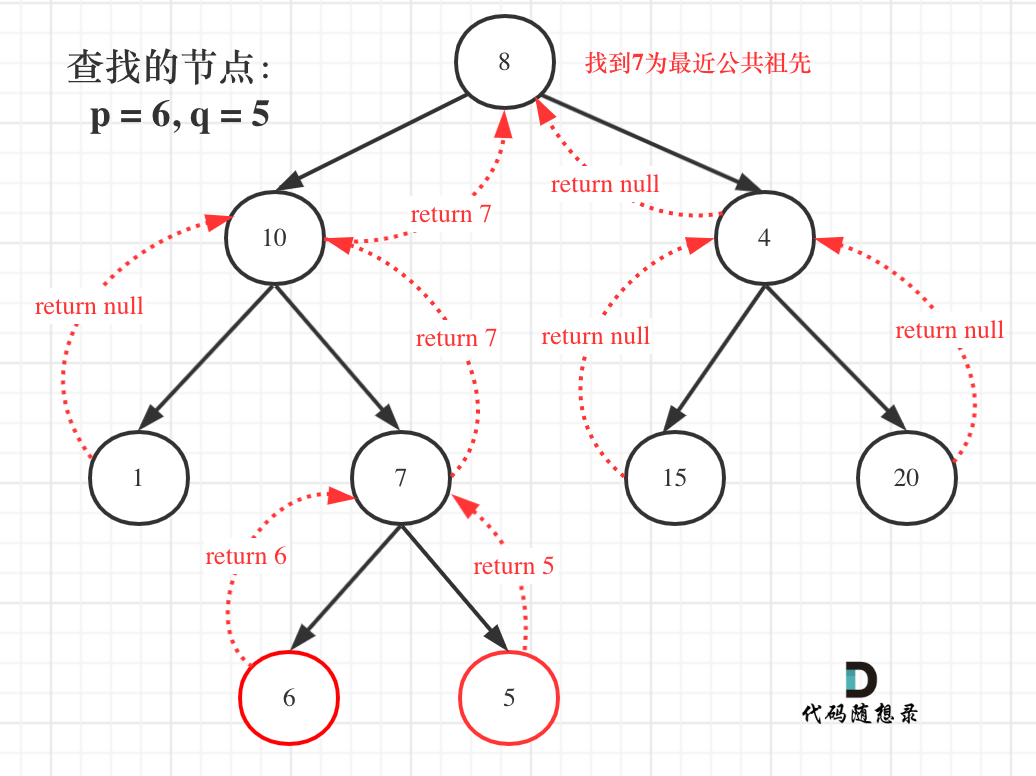
公共祖先的回溯

注意

leftValue == null ? rightValue : leftValue

就是

1
2
3
4
5
6
7
8
9
if(left == null && right == null) { // 若未找到节点 p 或 q
    return null;
}else if(left == null && right != null) { // 若找到一个节点
    return right;
}else if(left != null && right == null) { // 若找到一个节点
    return left;
}else { // 若找到两个节点
    return root;
}

1676. 二叉树的最近公共祖先 IV

本题 不再是p，q，而是一组node

只需要稍微修改一下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode[] nodes) {
    Set<Integer> hs = new HashSet<>();
    for (TreeNode node : nodes) {
        hs.add(node.val);
    }
    return findTargetsFromNodes(root, hs);
}

private TreeNode findTargetsFromNodes(TreeNode root, Set<Integer> nodes) {
    if (root == null) {
        return null;
    }

    // 依旧是找当前 root 是否本身即为最近公共祖先， 但是为了快速查找且题目要求node值都不相同，
    // 用 hashset来快速找值
    if (nodes.contains(root.val)) {
        return root;
    }

    TreeNode leftValue = findTargetsFromNodes(root.left, nodes);
    TreeNode rightValue = findTargetsFromNodes(root.right, nodes);

    if (leftValue != null && rightValue != null) {
        return root;
    }

    return leftValue != null ? leftValue : rightValue;
}

1644. 二叉树的最近公共祖先 II

之前的题目都说target节点都在树里，但是本题 不保证树里一定有p 和 q

那么，对于上边两道题在前序遍历位置时发现当前root节点和target值相等直接返回就不能用了，因为不能保证是不是另一个也存在，我们需要知道树的所有信息才行，也就是要在后序遍历的位置，即：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
boolean isPExist = false, isQExist = false;
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
    TreeNode ret = findTargetValues(root, p, q);
    if (!isQExist || !isPExist) return null;
    return ret;
}

private TreeNode findTargetValues(TreeNode root, TreeNode p, TreeNode q) {
    if (root == null) return null;

    TreeNode leftValue = findTargetValues(root.left, p, q);
    TreeNode rightValue = findTargetValues(root.right, p, q);

    if (leftValue != null && rightValue != null) {
        // 解决情况1，自身节点不是LCA
        return root;
    }

    if (root.val == p.val) {
        // 解决情况2，自身节点是LCA：
        isPExist = true;
        return root;
    }

    if (root.val == q.val) {
        isQExist = true;
        return root;
    }
    return leftValue == null ? rightValue : leftValue;
}

235. 二叉搜索树的最近公共祖先

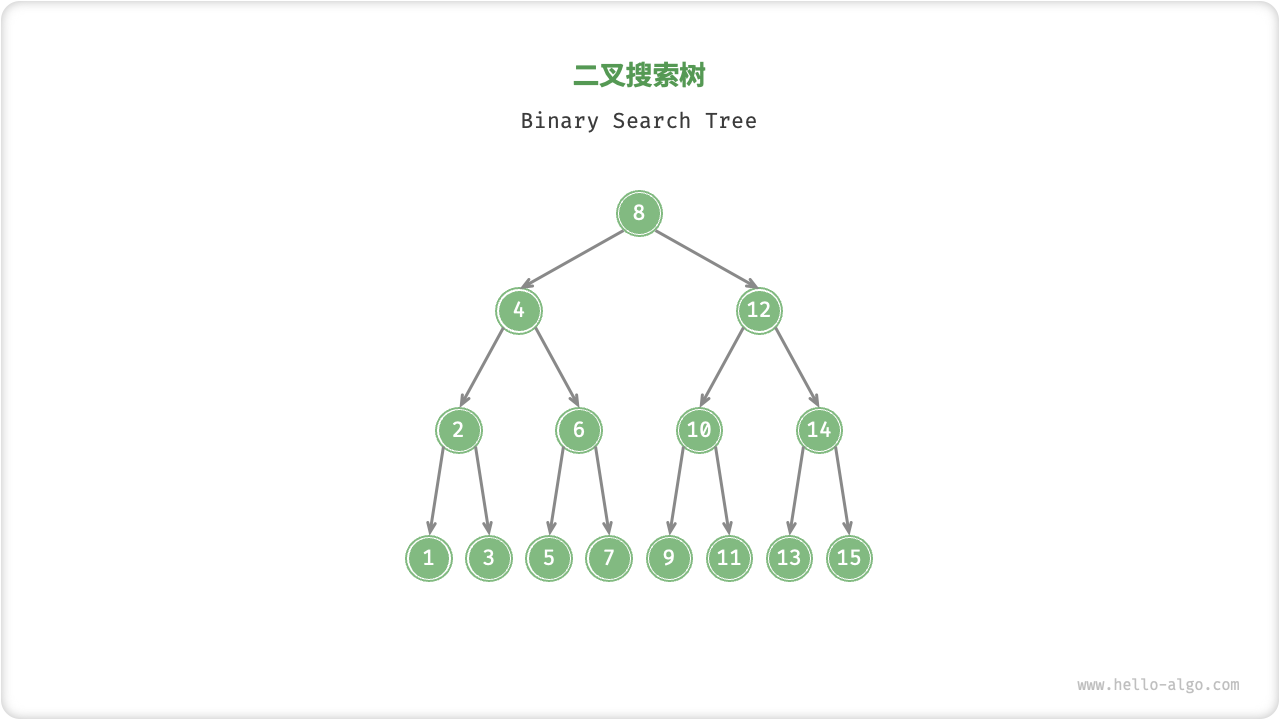
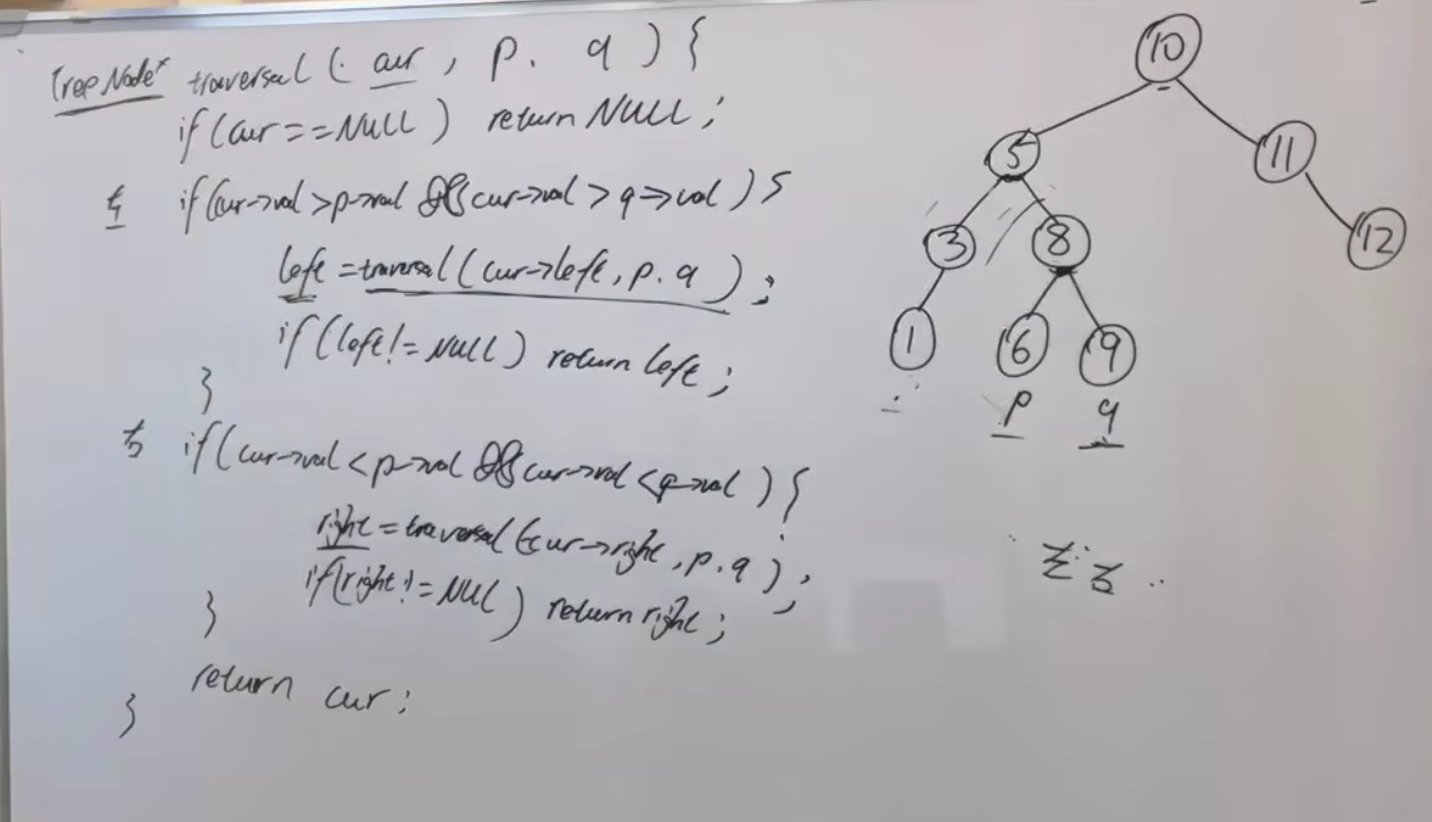
本题最重要的是利用BST的性质

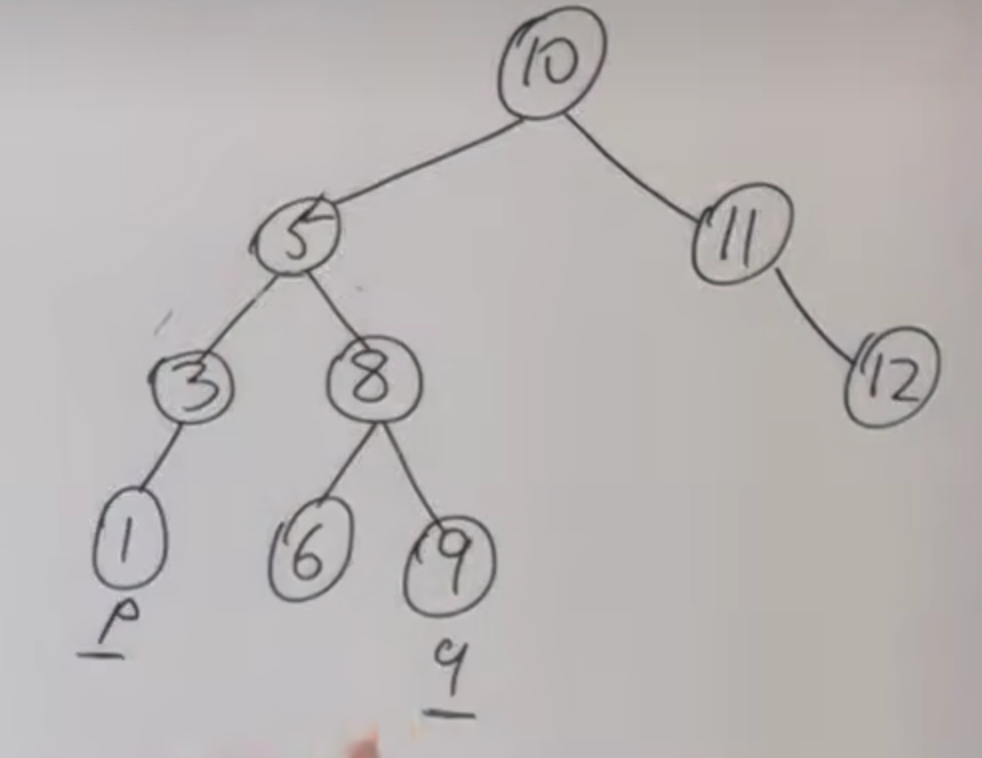
BST_公共祖先

  1. 当根节点值小于p和q 即 小于 p，q的最小值
    1. 说明要的公共祖先在右边的树里
  2. 当根节点值大于p和q 即 大于 p，q的最大值
    1. 说明要的公共祖先在左边的树里
  3. 当根节点介于中间时则一定为最近的公共祖先
    1. 为什么最近？
      1. 因为如果还要进行下去，要么往左走要么往右走总会丢失一个
      2. 按图中的例子，如果5下面还有更近的祖先，那么假设5往左走，那么会丢失q，同理，向右走则会丢失p

结论: Math.min(q.val, p.val) <= root.val <= Math.max(q.val, p.val)那么此时的root即为最近的公共祖先

pseudocode:

BST_公共祖先_伪代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
    int val1 = Math.min(p.val, q.val);
    int val2 = Math.max(p.val, q.val);
    return findTarget(root, val1, val2);
}

private TreeNode findTarget(TreeNode root, int val1, int val2) {
    if (root == null) return null;
    if (root.val < val1) {
        // 值太小了，应该去右边找
        return findTarget(root.right, val1, val2);
    } 

    if (root.val > val2) {
        // 值太大了， 应该去左边找
       return findTarget(root.left, val1, val2);
    }
    // root.val >= val1 root.val <= val2 此时就是一个合法的公共祖先
    return root;
}

1650. 二叉树的最近公共祖先 III

本题包含了对父节点的引用：

1
2
3
4
5
6
class Node {
    public int val;
    public Node left;
    public Node right;
    public Node parent;
}

这道题用的是链表合并的思路：

即让两个指针p1 指向A的指针，p2指向B的指针，能够同时到达相交节点 c1

用两个指针 p1 和 p2 分别在两条链表上前进，我们可以让 p1 遍历完链表 A 之后开始遍历链表 B，让 p2 遍历完链表 B 之后开始遍历链表 A，这样相当于「逻辑上」两条链表接在了一起。

链表合并

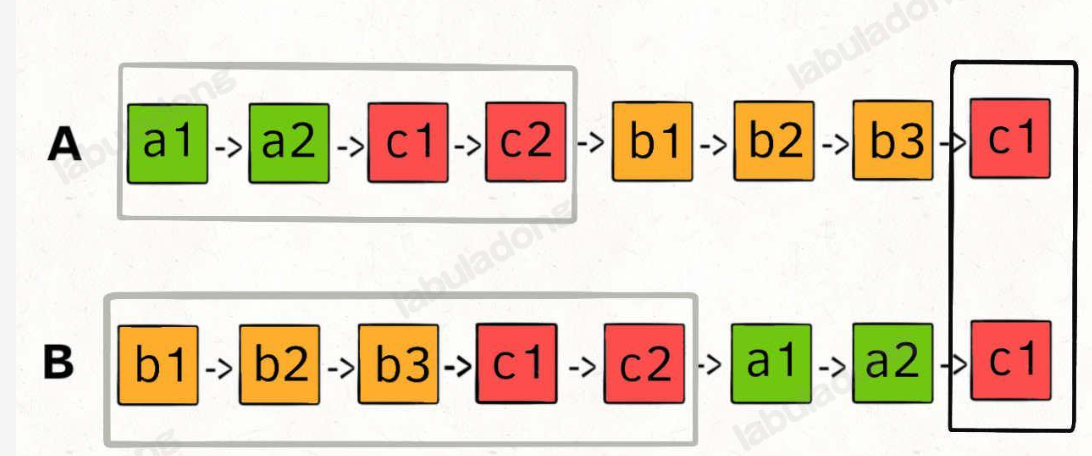
稍微替换一下，借用parent:

1
2
3
4
5
6
7
8
9
10
public Node lowestCommonAncestor(Node p, Node q) {
    Node pPointer = p, qPointer = q;
    while (pPointer != qPointer) {
        if (pPointer == null) pPointer = q;
        else pPointer = pPointer.parent;
        if (qPointer == null) qPointer = p;
        else qPointer = qPointer.parent;
    }
    return pPointer;
}