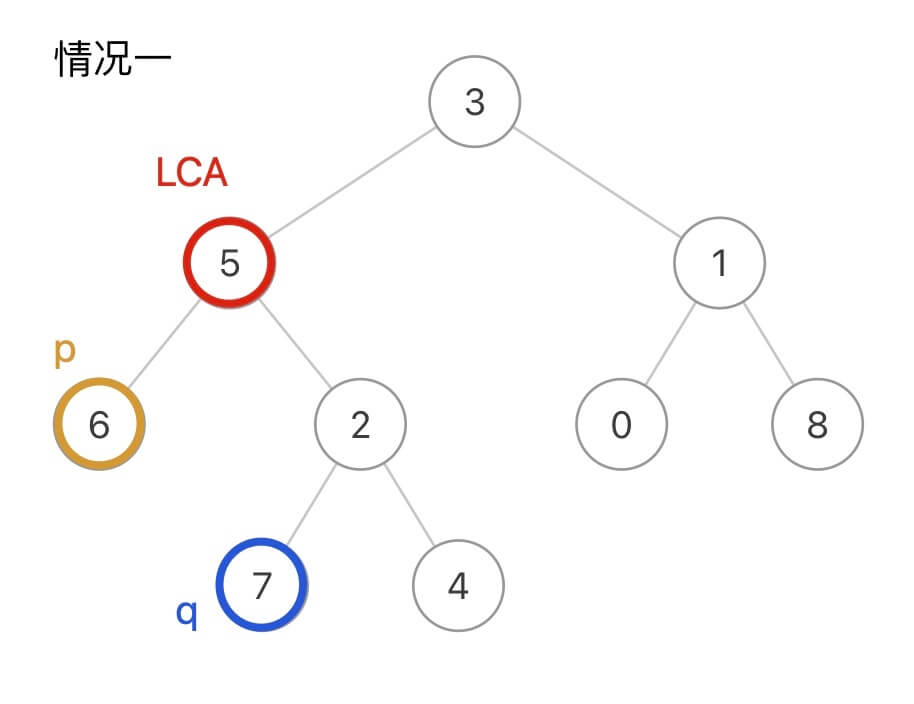
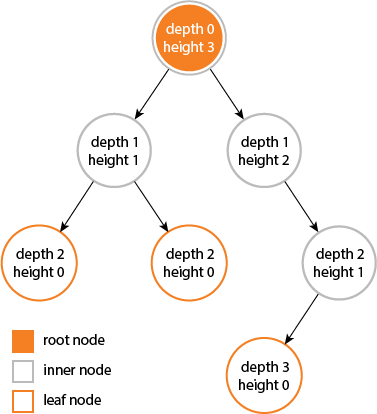
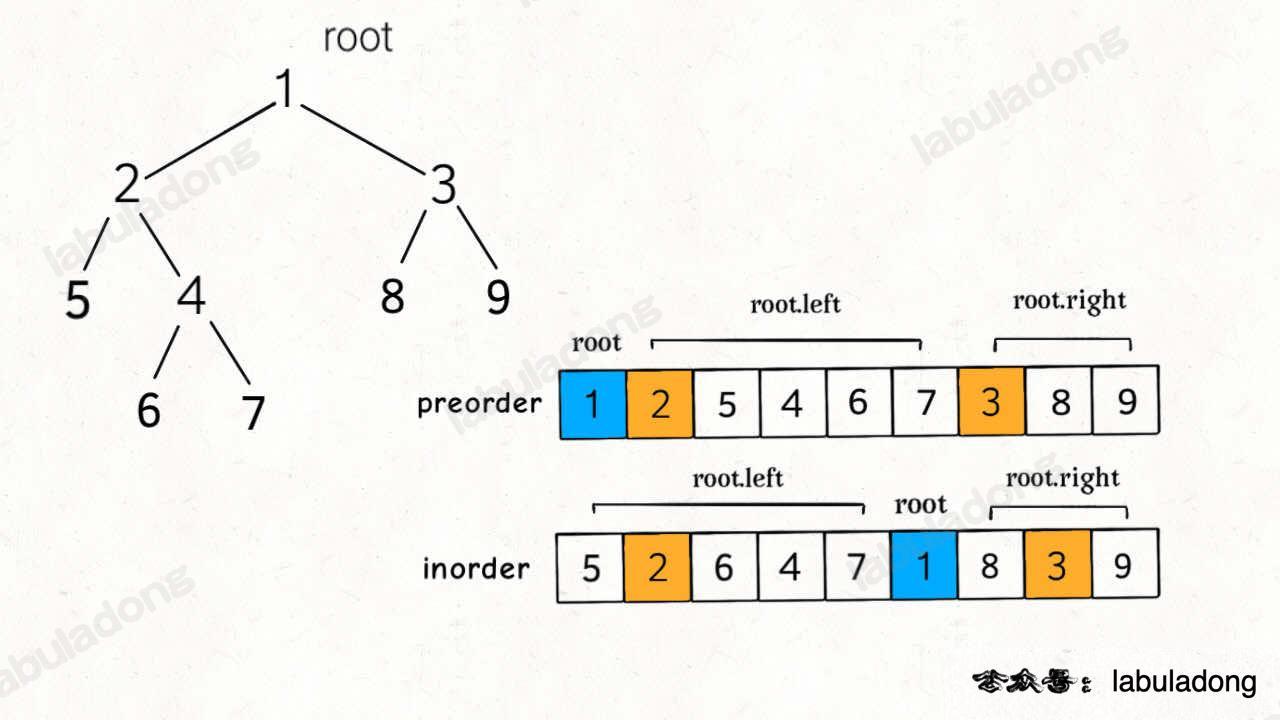
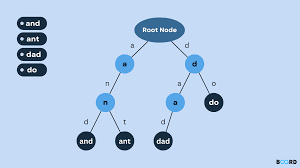
树计算深度类问题:
方法1 DFS:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| public int minDepth(TreeNode root) {
int res = dfsCompose(root);
return res;
}
private int dfsCompose(TreeNode cur) {
if(cur == null) return 0;
if(cur.left == null && cur.right == null) return 1;
int m1 = minDepth(cur.left);
int m2 = minDepth(cur.right);
if(cur.left == null || cur.right == null) return m1 + m2 + 1;
return Math.min(m1,m2) + 1;
}
private int dfsCompose(TreeNode cur, int curDepth) {
if (cur == null) return Integer.MAX_VALUE;
if (cur.left == null && cur.right == null) return curDepth;
int leftMin = dfsCompose(cur.left, curDepth + 1);
int rightMin = dfsCompose(cur.right, curDepth + 1);
return Math.min(leftMin, rightMin);
}
|
方法2 BFS
第一版:(⚠️有瑕疵)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| public int minDepth(TreeNode root) {
if (root == null) return 0;
int res = bfs(root);
return res;
}
private int bfs(TreeNode cur) {
int min = Integer.MAX_VALUE;
Deque<TreeNode> dq = new ArrayDeque<>();
dq.addLast(cur);
int height = 1;
while (!dq.isEmpty()) {
int len = dq.size();
for (int i = 0; i < len; i++) {
TreeNode levelCur = dq.pollFirst();
if (levelCur.left == null && levelCur.right == null) min = Math.min(min, height);
if (levelCur.left != null) dq.addLast(levelCur.left);
if (levelCur.right != null) dq.addLast(levelCur.right);
}
height++;
}
return min;
}
|
这个版本有瑕疵的原因是BFS第一个碰到的叶子结点一定是最短的。因为他是一层一层下去的
因此无需维护min, 可以直接return 所以可以优化为:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| public int minDepth(TreeNode root) {
if (root == null) return 0;
int res = bfs(root);
return res;
}
private int bfs(TreeNode cur) {
Deque<TreeNode> dq = new ArrayDeque<>();
dq.addLast(cur);
int height = 1;
while (!dq.isEmpty()) {
int len = dq.size();
for (int i = 0; i < len; i++) {
TreeNode levelCur = dq.pollFirst();
if (levelCur.left == null && levelCur.right == null) return height;
if (levelCur.left != null) dq.addLast(levelCur.left);
if (levelCur.right != null) dq.addLast(levelCur.right);
}
height++;
}
return height;
}
|
优化前:

优化后:
dfs的两个解法:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| public int maxDepth(TreeNode root) {
traverse(root);
return res == Integer.MIN_VALUE ? 0 : res;
}
private int getMax(TreeNode cur) {
if (cur == null) return 0;
int leftMax = getMax(cur.left);
int rightMax = getMax(cur.right);
int maxDepth = Math.max(leftMax, rightMax) + 1;
return maxDepth;
}
int depth = 0;
int res = Integer.MIN_VALUE;
private void traverse(TreeNode cur) {
if (cur == null) return;
depth++;
if (cur.left == null && cur.right == null) {
res = Math.max(depth, res);
}
traverse(cur.left);
traverse(cur.right);
depth--;
}
|
回溯:方法1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| public int maxDepth(Node root) {
if (root == null) return 0;
traverse(root);
return res + 1;
}
int res = Integer.MIN_VALUE;
int depth;
private void traverse(Node root) {
if (root == null) return;
if (root.children.size() == 0) {
res = Math.max(res, depth);
}
for (Node child : root.children) {
depth++;
traverse(child);
depth--;
}
}
|
回溯:格式2
⚠️注意depth的位置以及res在maxDepth中return的变化⚠️
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| public int maxDepth(Node root) {
if (root == null) return 0;
traverse(root);
return res;
}
int res = Integer.MIN_VALUE;
int depth;
private void traverse(Node root) {
if (root == null) return;
depth++;
if (root.children.size() == 0) {
res = Math.max(res, depth);
}
for (Node child : root.children) {
traverse(child);
}
depth--;
}
|