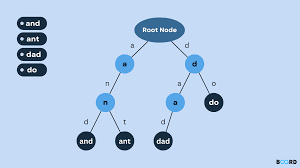
二叉树
定义概念:

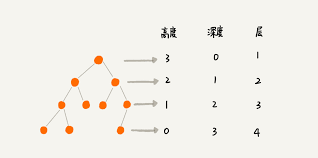
高度:二叉树中任意一个节点到叶子节点的距离 <- 经常用后序遍历解决问题
- 通过将子节点的高度返回给父节点父节点高度 +1 即可解决问题
深度:二叉树中任意一个节点到根节点的距离 <- 经常用前序遍历解决问题
思维方法:
遇到一道二叉树的题目时的通用思考过程是:
1、是否可以通过遍历一遍二叉树得到答案?如果可以,用一个 traverse 函数配合外部变量来实现。
2、是否可以定义一个递归函数,通过子问题(子树)的答案推导出原问题的答案?如果可以,写出这个递归函数的定义,并充分利用这个函数的返回值。
3、无论使用哪一种思维模式,你都要明白二叉树的每一个节点需要做什么,需要在什么时候(前中后序)做。
关于后序遍历:
后序遍历好在:前序位置的代码只能从函数参数中获取父节点传递来的数据,而后序位置的代码不仅可以获取参数数据,还可以获取到子树通过函数返回值传递回来的数据。
一旦发现题目和子树有关,那大概率要给函数设置合理的定义和返回值,在后序位置写代码了。
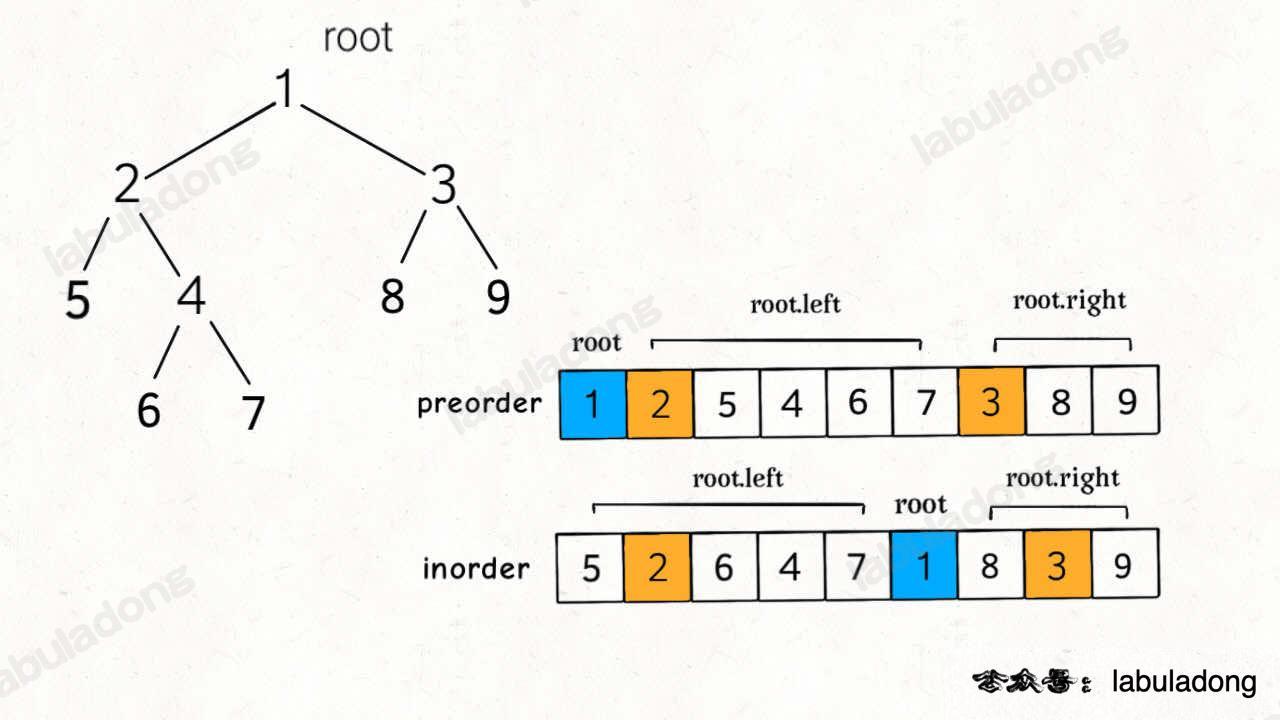
根据刷题经验的补充:可以尝试把树抽象成为数组,来看看用数组怎么解决问题
递归遍历
🤣 一入递归深似海,走到尽头出不来 :P
- 确定递归函数的参数和返回值
- 确定终止条件
- 确定单层递归的逻辑
例题
- 144.二叉树的前序遍历
- 145.二叉树的后序遍历
- 94.二叉树的中序遍历
核心就是 traverse function:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| public List<Integer> traversalMain(TreeNode root) {
List<Integer> res = new ArrayList<>();
traverse(root, res);
return res;
}
private void traverse(TreeNode cur, List<Integer> res) {
if (cur == null) return;
traverse(cur.left, res);
traverse(cur.right, res);
}
|
迭代遍历
其实就是用迭代法实现前中后序的遍历
前序 中左右
中序 左中右
后序 左右中
前序和后序可以归类为一种而中序略微有些差别:
前序和中序可以被归类为 类似于层序遍历的遍历:
对于前序来说由于我们需要的结果为 中左右 那么借助栈的先进后出的性质我们需要放入中/根 (pop) 右左:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| public List<Integer> preorderTraversal(TreeNode root) {
Deque<TreeNode> dq = new ArrayDeque<>();
List<Integer> res = new ArrayList<>();
if (root == null) return res;
dq.addLast(root);
while (!dq.isEmpty()) {
if (dq.peekLast() == null) break;
TreeNode cur = dq.pollLast();
res.add(cur.val);
if (cur.right != null) dq.addLast(cur.right);
if (cur.left != null) dq.addLast(cur.left);
}
return res;
}
|
对于后序遍历来说,我们只需要完成如下的操作:
- 调整层里的右左(前序) -> 左右(后序)
- 反转结果即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| public List<Integer> postorderTraversal(TreeNode root) {
Deque<TreeNode> dq = new ArrayDeque<>();
List<Integer> res = new ArrayList<>();
if (root == null) return res;
dq.addLast(root);
while (!dq.isEmpty()) {
if (dq.peekLast() == null) break;
TreeNode cur = dq.pollLast();
res.add(cur.val);
if (cur.left != null) dq.addLast(cur.left);
if (cur.right != null) dq.addLast(cur.right);
}
Collections.reverse(res);
return res;
}
|
中序遍历会有所不同,因为现在的中不在是上一层的根,而是需要左节点遍历完成后的祖先。因此,我们需要一个额外的遍历的指针来记录visit过的节点:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| public List<Integer> inorderTraversal(TreeNode root) {
Deque<TreeNode> dq = new ArrayDeque<>();
List<Integer> res = new ArrayList<>();
TreeNode cur = root;
while (!dq.isEmpty() || cur != null) {
if (cur != null) {
dq.addLast(cur);
cur = cur.left;
} else {
cur = dq.pollLast();
res.add(cur.val);
cur = cur.right;
}
}
return res;
}
|
统一后的迭代遍历
为了风格统一,来用以下的方法来做三序的迭代法本质上是用了标记法:就是要处理的节点放入栈之后,紧接着放入一个空指针作为标记。
中序遍历的标记法例子:

前序遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> result = new LinkedList<>();
Stack<TreeNode> st = new Stack<>();
if (root != null) st.push(root);
while (!st.empty()) {
TreeNode node = st.peek();
if (node != null) {
st.pop();
if (node.right!=null) st.push(node.right);
if (node.left!=null) st.push(node.left);
st.push(node);
st.push(null);
} else {
st.pop();
node = st.peek();
st.pop();
result.add(node.val);
}
}
return result;
}
}
|
中序遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> result = new LinkedList<>();
Stack<TreeNode> st = new Stack<>();
if (root != null) st.push(root);
while (!st.empty()) {
TreeNode node = st.peek();
if (node != null) {
st.pop();
if (node.right!=null) st.push(node.right);
st.push(node);
st.push(null);
if (node.left!=null) st.push(node.left);
} else {
st.pop();
node = st.peek();
st.pop();
result.add(node.val);
}
}
return result;
}
}
|
后序遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> result = new LinkedList<>();
Stack<TreeNode> st = new Stack<>();
if (root != null) st.push(root);
while (!st.empty()) {
TreeNode node = st.peek();
if (node != null) {
st.pop();
st.push(node);
st.push(null);
if (node.right!=null) st.push(node.right);
if (node.left!=null) st.push(node.left);
} else {
st.pop();
node = st.peek();
st.pop();
result.add(node.val);
}
}
return result;
}
}
|
层序遍历
核心:使用队列 因为有先入先出的性质 + 用 size 来维护队列(当前层的元素数量,从而保证元素是固定于这一层)
队列和栈真是好兄弟,队列来做BFS,栈来做DFS 😆

- 根节点入队
- loop while(!q.isempty())
- int len = q.size()
- while (Len– > 0)
例题:
- 102.二叉树的层序遍历
- 107.二叉树的层次遍历II
- 199.二叉树的右视图
- 637.二叉树的层平均值
- 429.N叉树的层序遍历
- 515.在每个树行中找最大值
- 116.填充每个节点的下一个右侧节点指针
- 117.填充每个节点的下一个右侧节点指针II
- 104.二叉树的最大深度
- 111.二叉树的最小深度
太多了… 仅需几道题详解
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| public List<List<Integer>> levelOrder(TreeNode root) {
Deque<TreeNode> dq = new ArrayDeque<>();
List<List<Integer>> res = new ArrayList<>();
if (root == null) return res;
dq.addLast(root);
while (!dq.isEmpty()) {
int size = dq.size();
List<Integer> cur = new LinkedList<>();
for (int i = 0; i < size; i++) {
TreeNode top = dq.pollFirst();
cur.add(top.val);
if (top.left != null) dq.addLast(top.left);
if (top.right != null) dq.addLast(top.right);
}
res.add(cur);
}
return res;
}
|
唯一的区别就是用linkedlist把一层的结果加到头部即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| public List<List<Integer>> levelOrderBottom(TreeNode root) {
LinkedList<List<Integer>> res = new LinkedList<>();
Deque<TreeNode> dq = new ArrayDeque<>();
if (root == null) return res;
dq.addLast(root);
while (!dq.isEmpty()) {
int size = dq.size();
List<Integer> cur = new LinkedList<>();
for (int i = 0; i < size; i++) {
TreeNode curNode = dq.pollFirst();
cur.add(curNode.val);
if (curNode.left != null) dq.add(curNode.left);
if (curNode.right != null) dq.add(curNode.right);
}
res.addFirst(cur);
}
return res;
}
|
例题
树计算深度类问题:
见 二叉树之计算深度 中包含计算深度类问题的习题以及思路
求节点和的问题
此题可以分解为三个问题:
- 求所有节点的和, 很简单,就是左右树的节点和加root节点
1
2
3
4
5
6
7
8
9
10
|
public int sumOfTrees(TreeNode root) {
if (root == null) {
return 0;
}
int leave = root.val;
int left = sumOfTrees(root.left);
int right = sumOfTrees(root.right);
return left + right + leave;
}
|
- 求所有叶子结点的和, 也很简单,就只是多了一个判断叶子结点的条件:
if (root.left == null && root.right == null)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
public int sumOfLeaves(TreeNode root) {
if (root == null) {
return 0;
}
int leave = 0;
if (root.left == null && root.right == null) {
leave = root.val;
}
int left = sumOfLeaves(root.left);
int right = sumOfLeaves(root.right);
return left + right + leave;
}
|
- 求左叶子结点的和, 也不难,无非是分成两步:
- 该节点是其父节点的左子节点。
- 该节点是一个叶子节点,即它没有左右子节点。
即:if (cur.left != null && cur.left.left == null && cur.left.right == null)
因此借助二叉树的思维框架我们可以用traverse + 额外变量的方式来解决问题:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| int sum = 0;
public int sumOfLeftLeaves(TreeNode root) {
if (root == null) return 0;
dfs(root);
return sum;
}
private void dfs(TreeNode cur) {
if (cur == null) return;
if (cur.left != null && cur.left.left == null && cur.left.right == null) {
sum += cur.left.val;
}
dfs(cur.left);
dfs(cur.right);
}
|
构造类问题
见 二叉树之构造类问题 中包含构造类问题的习题以及思路
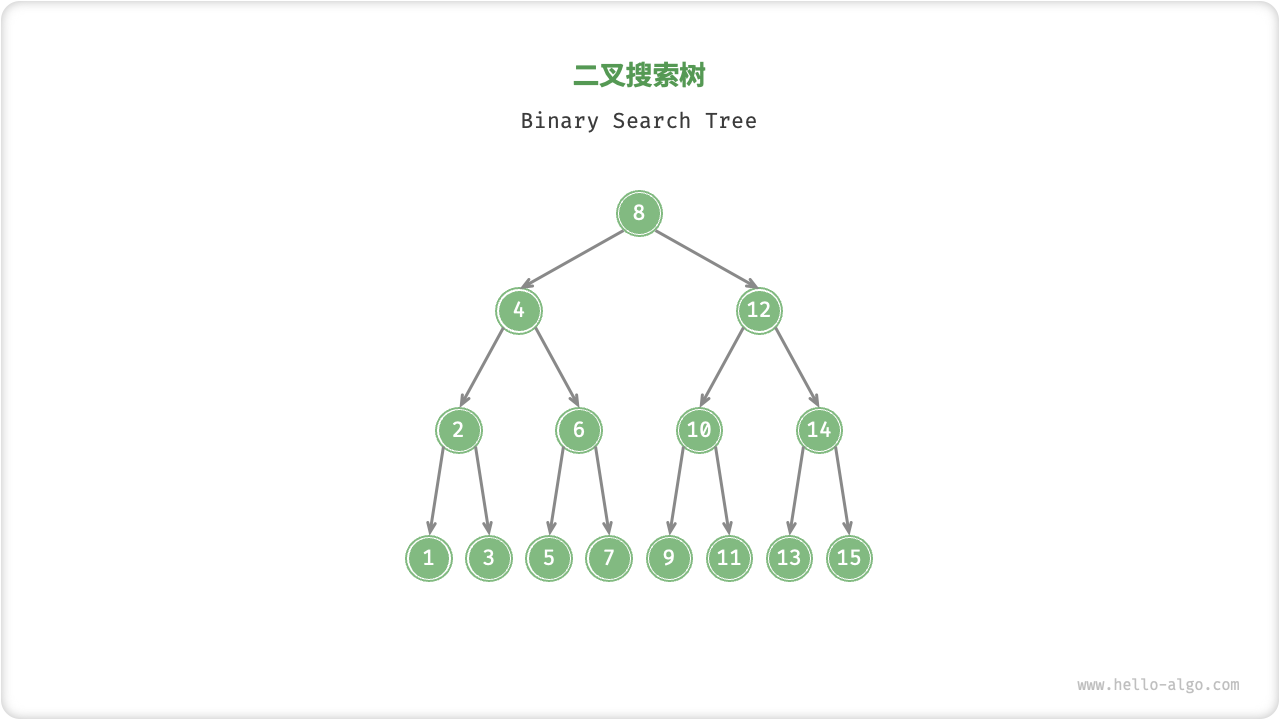
BST 二叉搜索树相关题目
见 二叉搜索树 中包含二叉搜索树问题的习题以及思路
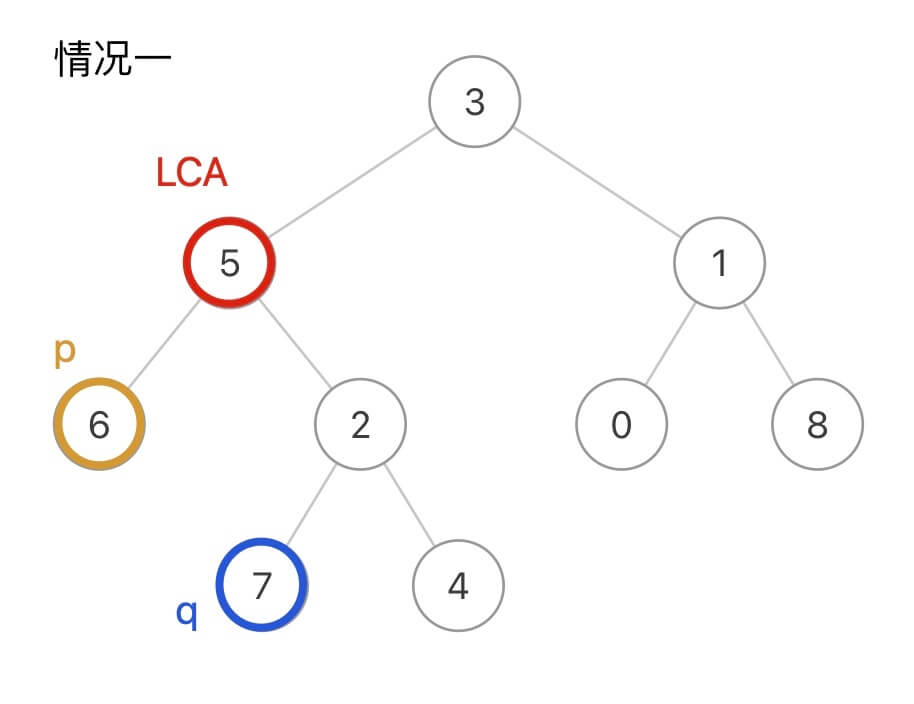
二叉树公共祖先
见 二叉树之公共祖先 中包含公共祖先的习题以及思路
其他例题
二叉树的递归分为「遍历」和「分解问题」两种思维模式,这道题可以同时使用两种思维模式。
方法1: 递归 - 分解问题
第一个自己写出来的递归,‼️终于‼️感受到为什么说递归讲究的就是一个自信 😆
1
2
3
4
5
6
7
8
9
10
11
12
13
| public TreeNode invertTree(TreeNode root) {
TreeNode res = dfs(root);
return res;
}
private TreeNode dfsQuestionsDivide(TreeNode cur) {
if (cur == null) return null;
TreeNode leftSwappedResult = dfsQuestionsDivide(cur.left);
TreeNode rightSwappedResult = dfsQuestionsDivide(cur.right);
cur.left = rightSwappedResult;
cur.right = leftSwappedResult;
return cur;
}
|
方法2: 递归 - 遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| public TreeNode invertTree(TreeNode root) {
TreeNode res = dfsTraverse(root);
return res;
}
private TreeNode dfsTraverse(TreeNode cur) {
if (cur == null) return null;
TreeNode tmp = cur.left;
cur.left = cur.right;
cur.right = tmp;
dfsTraverse(cur.left);
dfsTraverse(cur.right);
return cur;
}
|
这是一道backtrack的题,这里我先给出代码再解释为什么 root.left后没有 显性 的removeLast() 操作
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| public List<String> binaryTreePaths(TreeNode root) {
LinkedList<String> res = new LinkedList<>();
LinkedList<String> nodesList = new LinkedList<>();
backtrack(root, res, nodesList);
return res;
}
private void backtrack(TreeNode root, List<String> res, LinkedList<String> nodesList) {
if (root == null) return;
if (root.left == null && root.right == null) {
nodesList.addLast(String.valueOf(root.val));
String s = String.join("->", nodesList);
res.add(s);
nodesList.removeLast();
}
nodesList.addLast(String.valueOf(root.val));
backtrack(root.left, res, nodesList);
backtrack(root.right, res, nodesList);
nodesList.removeLast();
}
|
假设我们有以下二叉树:
当我们调用 traverse(root) 时,执行顺序如下:
- 添加 1 到
path,此时 path = [1]。
- 调用
traverse(root.left) 以遍历左子树(节点 2)。
- 添加 2 到
path,此时 path = [1, 2]。
- 调用
traverse(root.left) 以遍历左子树(节点 4)。
- 添加 4 到
path,此时 path = [1, 2, 4]。
- 4 是叶子节点,将
path 添加到 res,执行 path.removeLast(),从 path 中移除 4,此时 path = [1, 2]。
- 返回上一层递归调用(节点 2)。
- 调用
traverse(root.right) 以遍历右子树(节点 5)。
- 添加 5 到
path,此时 path = [1, 2, 5]。 ii. 5 是叶子节点,将 path 添加到 res,执行 path.removeLast(),从 path 中移除 5,此时 path = [1, 2]。 iii. 返回上一层递归调用(节点 2)。
- 在后序遍历位置,执行
path.removeLast(),从 path 中移除 2,此时 path = [1]。
- 调用
traverse(root.right) 以遍历右子树(节点 3)。
- 添加 3 到
path,此时 path = [1, 3]。
- 3 是叶子节点,将
path 添加到 res,执行 path.removeLast(),从 path 中移除 3,此时 path = [1]。
- 在后序遍历位置,执行
path.removeLast(),从 path 中移除 1,此时 path 为空。
在这个例子中,我们可以看到,在每次递归调用返回时,path.removeLast() 都会被执行。这样,我们可以确保在遍历过程中,path 变量始终正确地表示从根节点到当前节点的路径。在遍历左子树(节点 2)时,path.removeLast() 被执行了两次:一次是在遍历节点 4 后,另一次是在遍历节点 5 后。这样,我们可以确保在遍历右子树(节点 3)之前,path 变量已经从左子树遍历的影响中恢复。这可以确保在继续遍历过程时,path 变量正确地表示从根节点到当前节点的路径。
继续遍历右子树(节点 3):
- 调用
traverse(root.right) 以遍历右子树(节点 3)。
- 添加 3 到
path,此时 path = [1, 3]。
- 3 是叶子节点,将
path 添加到 res,执行 path.removeLast(),从 path 中移除 3,此时 path = [1]。
- 在后序遍历位置,执行
path.removeLast(),从 path 中移除 1,此时 path 为空。
现在,整个树的遍历已经完成,res 变量包含了所有从根节点到叶子节点的路径,即 ["1->2->4", "1->2->5", "1->3"]。
这道题很多知识点,涉及到了前缀和的一些理解:
我们需要一个 哈希表 来存储前缀和的个数,由于这道题只需要返回答案个数,所以记录个数即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| class Solution {
Map<Long, Integer> hmPrefixCount = new HashMap<>();
int targetSum;
long curSum = 0L;
public int pathSum(TreeNode root, int targetSum) {
hmPrefixCount.put(0L ,1);
this.targetSum = targetSum;
return traverse(root);
}
private int traverse(TreeNode root) {
if (root == null) return 0;
curSum += root.val;
int res = 0;
res += hmPrefixCount.getOrDefault(curSum - targetSum, 0);
hmPrefixCount.put(curSum, hmPrefixCount.getOrDefault(curSum, 0) + 1);
int leftTotal = traverse(root.left);
int rightTotal = traverse(root.right);
res = res + leftTotal + rightTotal;
hmPrefixCount.put(curSum, hmPrefixCount.get(curSum) - 1);
curSum -= root.val;
return res;
}
}
|
其中我认为最不好理解的:
1
| res += hmPrefixCount.getOrDefault(curSum - targetSum, 0);
|
- 为什么是
curSum - targetSum?
这是因为:
假设我们有以下路径:
从 X 到 Y 的路径和为 target,即 X + D + Y = target。
从 A 到 Y 的整个路径和为 curSum,即 A + B + X + D + Y = curSum。
我们的目标是找到从 A 到哪里的路径和,使得剩下的路径和(即从那个位置到 Y)等于 target。如果我们把这个位置称为 Z,那么 Z 就是 X 的前一个位置,即 B。
为了得到从 A 到 Z(即 B)的路径和,我们可以这样算:
从 A 到 Y 的路径和减去从 X 到 Y 的路径和,得到:
A + B = curSum - (X + D + Y)
这确实是 A 到 B 的路径和,不是到 X。因此,curSum - target 表示的是从 A 到 B 的路径和。这意味着从 X 开始到 Y 结束的路径和等于 target。
- 为什么这么找而不直接找哪一段路径和为target?
直接找哪个路径和等于 target 的确是一种方法,但效率不高。为了找到所有与 target 相等的路径和,你必须从每个节点开始,并考虑所有可能的子路径,这导致了O(n^2)的复杂性,其中n是树的节点数。
使用 prefixMap 和当前累加和 curSum 的方法优化了这个搜索过程。原因如下:
连续子数组问题的解决思路:这个问题与数组中找连续子数组和等于某个数的问题非常相似。在数组问题中,我们使用一个累加和来记录从数组开始到当前位置的所有元素的和,然后使用一个哈希表来记录之前看到的所有累加和。这种方法可以在O(1)的时间内判断是否存在一个子数组的和等于目标值。
时间复杂度:通过使用 prefixMap,我们可以在O(n)的时间复杂度内解决这个问题。对于每个节点,我们只需要O(1)的时间来更新 prefixMap 和查找 curSum - target。
记录所有前缀和:通过在遍历过程中记录所有可能的前缀和及其出现的次数,我们可以迅速地知道从当前节点回溯到之前的任何节点的路径和是否等于 target。
所以,使用这种方法比直接搜索效率更高,因为它利用了哈希表的查找能力,大大提高了搜索速度。
利用了后序遍历的特性 – 即我们可以从后续位置得到信息
以及ArrayList<>(1)是创建了一个size为1的list而不是里面有一个1
若想创建一个list里面有一个1: Arrays.asList(1);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
|
class Solution {
int distance;
int res = 0;
public int countPairs(TreeNode root, int distance) {
this.distance = distance;
dfsDepth(root);
return res;
}
private List<Integer> dfsDepth(TreeNode root) {
if (root == null) return new ArrayList<>();
if (root.left == null && root.right == null) {
return Arrays.asList(1);
}
List<Integer> nodeLeftList = dfsDepth(root.left);
List<Integer> nodeRightList = dfsDepth(root.right);
for (int leftLen : nodeLeftList) {
for (int rightLen : nodeRightList) {
if (leftLen + rightLen <= distance) {
this.res++;
}
}
}
List<Integer> all = new ArrayList<>();
for (int leftLen : nodeLeftList) {
leftLen++;
all.add(leftLen);
}
for (int rightLen : nodeRightList) {
rightLen++;
all.add(rightLen);
}
return all;
}
}
|