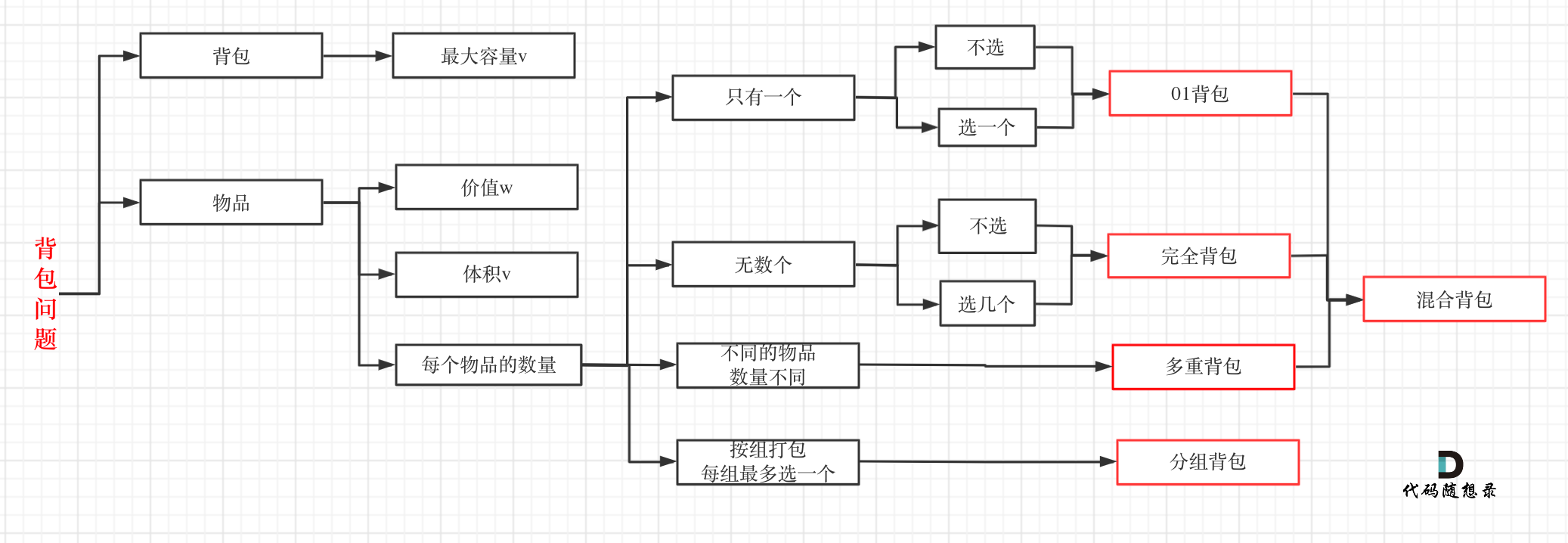
模板
一定有的参数
i, lowerBound (limitLow), UpperBound (limitHigh)
lowerBound, UpperBound在函数中一般不变化
前导零:
如果是数位比较,所以需要前补零 (一般为补充下界前导零)
反之如果是求各数位的和那么此时前导零没有影响所以不用补零
根据题目的要求来更新答案
例题 2843. 统计对称整数的数目
无记忆化搜索:纯模板:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 class Solution { String lowStr; String highStr; public int countSymmetricIntegers (int low, int high) { lowStr = String.valueOf(low); int nLow = lowStr.length(); highStr = String.valueOf(high); for (int i = 0 ; i < highStr.length() - nLow; i++) { lowStr = "0" + lowStr; } return digitDPDFS(0 , true , true , -1 , 0 , 0 ); } private int digitDPDFS (int i, boolean limitLow, boolean limitHigh, int start, int prevSum, int afterSum) { if (i == highStr.length()) { if (prevSum == afterSum) return 1 ; else return 0 ; } int lowerBound; if (limitLow) lowerBound = lowStr.charAt(i) - '0' ; else lowerBound = 0 ; int higherBound; if (limitHigh) higherBound = highStr.charAt(i) - '0' ; else higherBound = 9 ; if (start < 0 && (highStr.length() - i) % 2 > 0 ) { return lowerBound > 0 ? 0 : digitDPDFS(i + 1 , true , false , start, prevSum, afterSum); } int res = 0 ; boolean isLeft = start < 0 || i < (start + highStr.length()) / 2 ; for (int d = lowerBound; d <= higherBound; d++) { if (isLeft) prevSum += d; else afterSum += d; res += digitDPDFS( i + 1 , limitLow && d == lowerBound, limitHigh && d == higherBound, start < 0 && d > 0 ? i : start, prevSum, afterSum); if (isLeft) prevSum -= d; else afterSum -= d; } return res; } }
含有memo的
2719. 统计整数数目
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 class Solution { static int MOD = 1000000000 + 7 ; int min_sum, max_sum; char [] num1Char, num2Char; int n; int [][][] memo; public int count (String num1, String num2, int min_sum, int max_sum) { this .min_sum = min_sum; this .max_sum = max_sum; while (num1.length() < num2.length()) { num1 = "0" + num1; } num1Char = num1.toCharArray(); num2Char = num2.toCharArray(); n = num2Char.length; memo = new int [n][2 ][max_sum + 1 ]; for (int [][] mat : memo) { for (int [] row : mat) { Arrays.fill(row, -1 ); } } return dfs(0 , true , true , false , 0 ); } private int dfs (int i, boolean limitLow, boolean limitHigh, boolean isNum, int curSum) { if (i == n) { if (curSum >= this .min_sum && curSum <= this .max_sum) return 1 ; else return 0 ; } if (curSum > this .max_sum) return 0 ; if (!limitLow && !limitHigh && memo[i][isNum ? 1 : 0 ][curSum] != -1 ) { return memo[i][isNum ? 1 : 0 ][curSum]; } int res = 0 ; if (!isNum && num1Char[i] == '0' ) { res = (dfs(i + 1 , true , false , false , curSum)) % MOD; } int lowerBound = limitLow ? num1Char[i] - '0' : 0 ; int upperBound = limitHigh ? num2Char[i] - '0' : 9 ; int d0 = isNum ? 0 : 1 ; for (int d = Math.max(d0, lowerBound); d <= upperBound; d++) { res = (res + dfs(i + 1 , limitLow && d == lowerBound, limitHigh && d == upperBound, true , curSum + d)) % MOD; } if (!limitLow && !limitHigh) { memo[i][isNum ? 1 : 0 ][curSum] = res; } return res; } }
1399. 统计最大组的数目
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 class Solution { String nStr; Map<Integer, Integer> hm = new HashMap <>(); int [][] memo; public int countLargestGroup (int n) { nStr = String.valueOf(n); digitDP(0 , true , 0 ); int res = 1 ; int maxValue = -1 ; for (int value : hm.values()) { if (value > maxValue) { res = 1 ; maxValue = value; } else if (value == maxValue) res++; } return res; } private void digitDP (int i, boolean limitHigh, int digitSum) { if (i == nStr.length()) { if (digitSum > 0 ) { hm.merge(digitSum, 1 , (a, b) -> a + b); } return ; } int upperBound = limitHigh ? nStr.charAt(i) - '0' : 9 ; for (int d = 0 ; d < upperBound + 1 ; d++) { digitDP(i + 1 , limitHigh && d == upperBound, digitSum + d); } } } class Solution { public int countLargestGroup (int n) { char [] s = String.valueOf(n).toCharArray(); int m = s.length; int [][] memo = new int [m][m * 9 + 1 ]; for (int [] row : memo) { Arrays.fill(row, -1 ); } int maxCnt = 0 ; int ans = 0 ; for (int target = 1 ; target <= m * 9 ; target++) { int cnt = dfs(0 , target, true , s, memo); if (cnt > maxCnt) { maxCnt = cnt; ans = 1 ; } else if (cnt == maxCnt) { ans++; } } return ans; } private int dfs (int i, int left, boolean limitHigh, char [] s, int [][] memo) { if (i == s.length) { return left == 0 ? 1 : 0 ; } if (!limitHigh && memo[i][left] != -1 ) { return memo[i][left]; } int hi = limitHigh ? s[i] - '0' : 9 ; int res = 0 ; for (int d = 0 ; d <= Math.min(hi, left); d++) { res += dfs(i + 1 , left - d, limitHigh && d == hi, s, memo); } if (!limitHigh) { memo[i][left] = res; } return res; } }
两个问题:
为什么 target 的最大值是 9 * m
在这道题中,我们关注的是每个数字的 数位和 ,比如:
123 的数位和是 1 + 2 + 3 = 6999 的数位和是 9 + 9 + 9 = 27
m 是 n 的位数你已经通过:
1 2 char [] s = String.valueOf(n).toCharArray();int m = s.length;
得到了 n 的位数是 m。
每一位的数值最大是 9
十进制中,一个数的每一位最多是 9。所以,m 位数的最大数位和是:
1 9 + 9 + ... + 9 (m 个 9) = 9 * m
所以:当你在枚举 target 的时候
1 for (int target = 1 ; target <= m * 9 ; target++)
你是在枚举所有 可能出现的数位和 (从 1 到最大值 9 * m),这也就是这个区间的由来。
如果 n = 9999,那:
它是 4 位数 → m = 4
每一位最大是 9 → 最大数位和 = 4 * 9 = 36
所以 target 最大枚举到 36 是没问题的
为什么要把 left 定义成剩余的数位和 ,而不是已填的数位和 ?target = 1, 2, ..., 9*m 复用同一个记忆化搜索的结果 。0 累加到 target,那么 memo 的内容就和 target 绑定,无法复用 。
我们定义 dfs(i, left) 表示从第 i 位开始,还剩下 left 的数位和要分配。
这个“剩余”写法的好处是:
每次递归的目标结构是统一的 ,只和剩余值有关。所有 target 值之间的搜索过程是可以共用的。
假设定义:
这样做的问题是:
每个 target 都要单独从 sum = 0 开始递归;
那么你记忆化的 memo[i][sum] 是专门为这个 target 服务的;
切换 target 后,memo 不能复用 → 大量重复计算!
假设我们要处理 n = 99 → 两位数 → 最大 target 是 9 * 2 = 18
我们要枚举所有 target = 1~18,看哪些数(在 1~99 范围内)数位和等于 target。
我们用的是:
例如:
处理 target = 10 的时候会调用:
1 2 3 dfs(0, 10) dfs(1, 3) ...
处理 target = 12 的时候也会调用:
1 2 3 dfs(0, 12) dfs(1, 3) ←这个子问题可以复用之前 target=10 的 dfs(1,3) 结果 ...
如果是:
处理 target = 10 和 target = 12 时会分别从 curSum = 0 开始向上累加。curSum = 3 是在不同的路径、不同的目标下产生的 → 所以memo 无法共用 ,只能重新算。
一个详细例子 比如 n = 99:为什么 dfs(1, 3) 会在多个 target 中被共用。
我们处理的问题是:
我们使用数位 DP 来统计对于某个 target(数位和)来说,有多少个 x 满足:
我们定义:
i:当前正在填第几位(从左往右)left:还需要填的数位和limitHigh:是否受限于原数字 s 的上界(true 代表必须 ≤ n 对应位)
为什么处理 target=10 和 target=12 时,某些子状态(比如 dfs(1, 3)) 是可以共用的 。
我们从:
开始递归。第一位最多填 9,我们可以枚举 d=0 到 9:
类似地:
枚举第一位是 9 时,还剩下:
所以会递归到:
无论是从 target=10 还是 target=12 出发,它们都可能在中间产生:
因为这个状态只和「当前是第1位」+「还需要填3的和」+「不受限」有关
如果换成:
那 target = 10 和 target = 12 的时候,它们的起点不同:
dfs(0, 0, 10)
dfs(0, 0, 12)
在后续过程中你会分别得到 dfs(1, 3, 10) 和 dfs(1, 3, 12)
虽然当前和是 3,但是目标不一样,无法共用状态 。
因为 dfs(1, 3) 的含义是:
“从i = 1位(第二位)开始,构造所有数位和为3的合法组合”。
这和前面选的是哪个 target 无关,它只关心 当前位置 和 还剩下多少和要凑 。