什么是最小生成树 MST

先说「树」和「图」的根本区别：树不会包含环，图可以包含环。

什么是图的「生成树」呢，就是在图中找一棵包含图中的所有节点的树。专业点说，生成树是含有图中所有顶点的「无环连通子图」。

MST_0

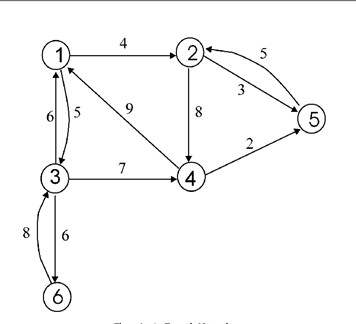
对于加权图，每条边都有权重，所以每棵生成树都有一个权重和。比如上图，右侧生成树的权重和显然比左侧生成树的权重和要小。

最小生成树: 所有可能的生成树中，权重和最小的那棵生成树就叫「最小生成树」。

Kruskal

MST 要保证边：

1、包含图中的所有节点。

2、形成的结构是树结构（即不存在环）。

3、权重和最小。

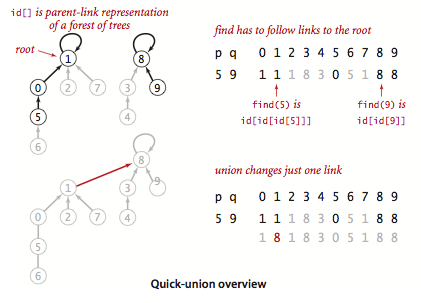
其中 1， 2可以用并查集来做：

对于添加的这条边，如果该边的两个节点本来就在同一连通分量里，那么添加这条边会产生环；反之，如果该边的两个节点不在同一连通分量里，则添加这条边不会产生环。

详见：并查集习题261

对于3:

用到了贪心思路：

将所有边按照权重从小到大排序，从权重最小的边开始遍历，如果这条边和 mst 中的其它边不会形成环，则这条边是最小生成树的一部分，将它加入 mst 集合；否则，这条边不是最小生成树的一部分，不要把它加入 mst 集合。

To be write…

1135

1584