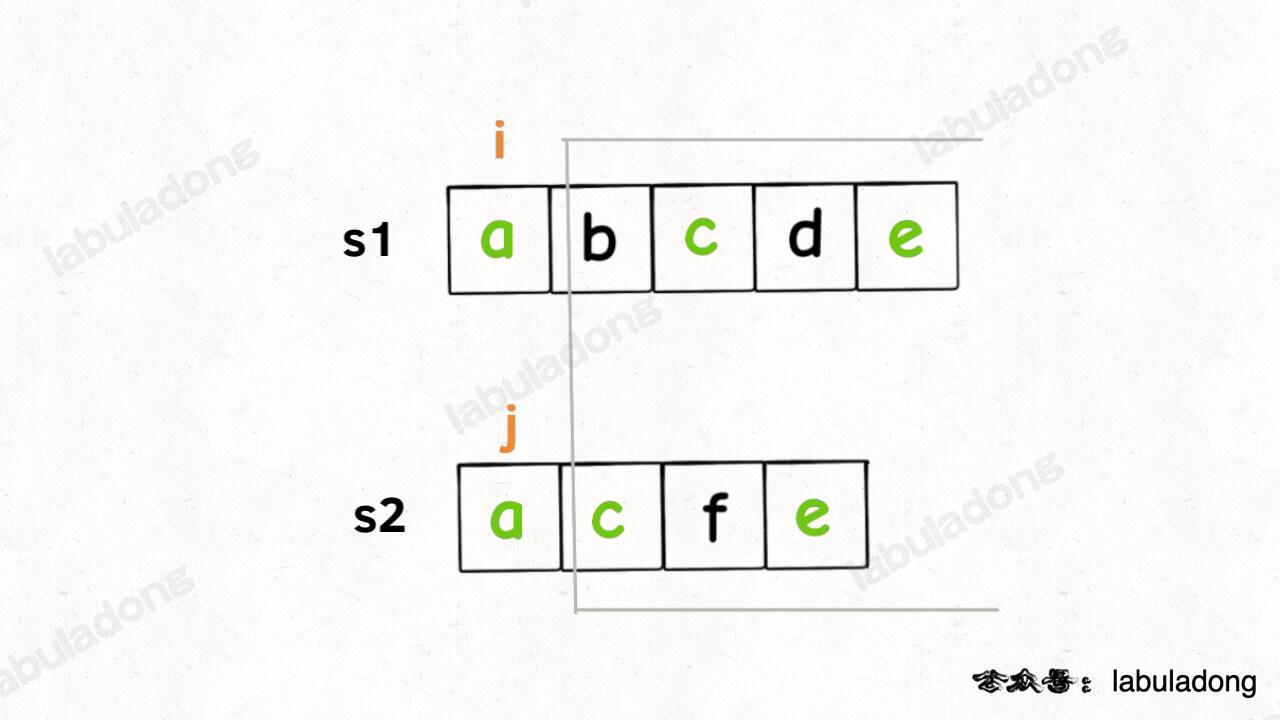
对于两个字符串求子序列的问题,都是用两个指针 i 和 j 分别在两个字符串上移动,大概率是动态规划思路。
labuladong-最长公共子序列
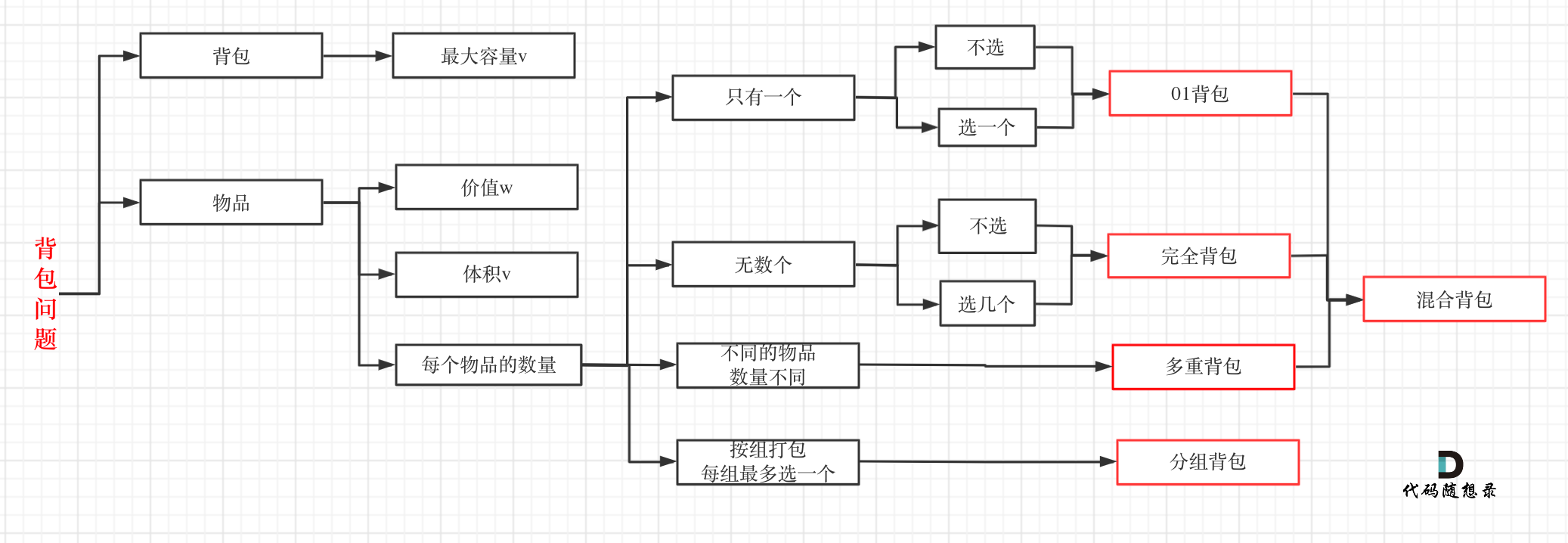
相关题目
1143. 最长公共子序列
583. 两个字符串的删除操作
712. 两个字符串的最小ASCII删除和
思路
定义dp(s1, i, s2, j)为s1[i...] 和 s2[j...]的最长公共子序列长度
goal: dp(s1, 0, s2, 0) 从零开始的最长公共子序列长度
base case: i == len(s1) 或 j == len(s2) 由于相当于没有string,所以最长公共子序列长度为0
状态转移:
在选的情况下,即charAt[i] == charAt[j]时,状态转移:
在不选的情况下可以从三种情况转移:
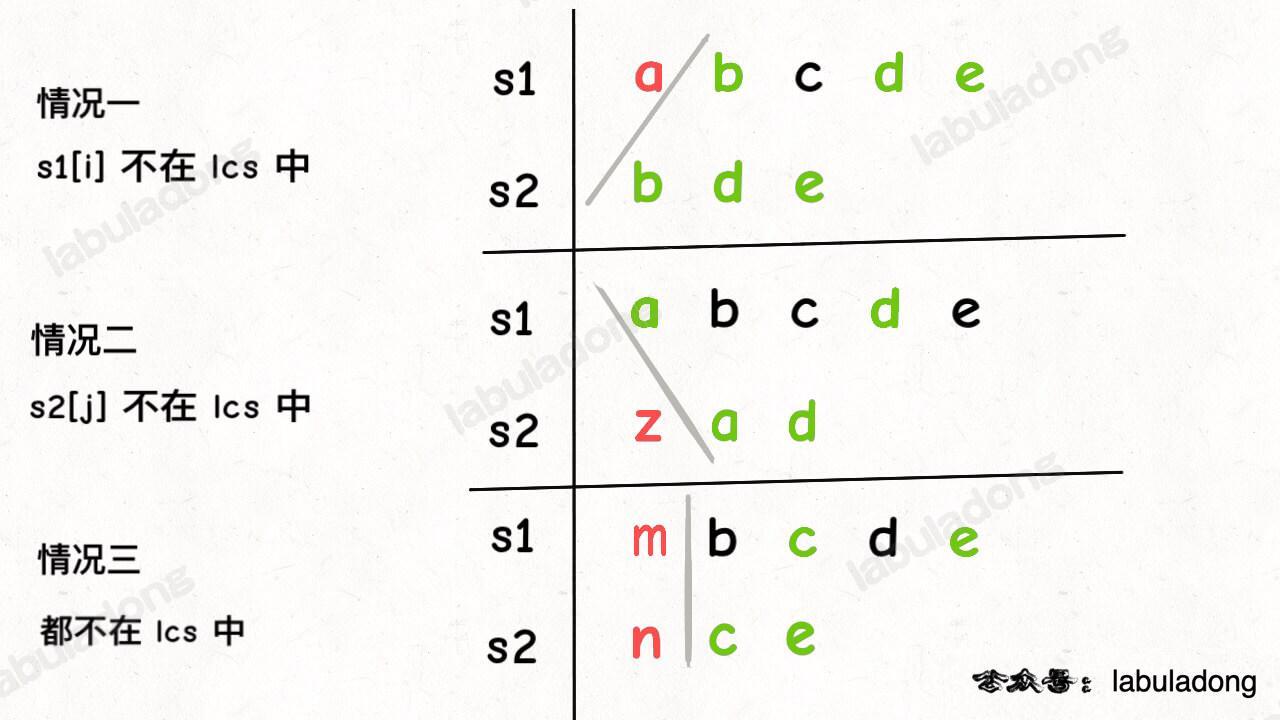
但是其实只有情况一和情况二,因为情况三被情况一cover了
模板题
代码:
自顶向下的递归解法:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| class Solution {
String text1, text2;
int m, n;
int[][] memo;
public int longestCommonSubsequence(String text1, String text2) {
m = text1.length();
n = text2.length();
memo = new int[m][n];
for (int i = 0; i < m; i++) {
Arrays.fill(memo[i], -1);
}
this.text1 = text1;
this.text2 = text2;
return dp(0, 0);
}
private int dp(int i, int j) {
if (i == m || j == n) return 0;
if (memo[i][j] != -1) return memo[i][j];
if (text1.charAt(i) == text2.charAt(j)) {
memo[i][j] = dp(i + 1, j + 1) + 1;
} else {
memo[i][j] = Math.max(
dp(i + 1, j),
dp(i, j + 1)
);
}
return memo[i][j];
}
}
|
自底向上的迭代解法:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| class Solution {
public int longestCommonSubsequence(String s1, String s2) {
int m = s1.length(), n = s2.length();
int[][] dp = new int[m + 1][n + 1];
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
if (s1.charAt(i - 1) == s2.charAt(j - 1)) {
dp[i][j] = 1 + dp[i - 1][j - 1];
} else {
dp[i][j] = Math.max(dp[i][j - 1], dp[i - 1][j]);
}
}
}
return dp[m][n];
}
}
|
变换一下思路,我们要的就是让他们成为他们的公共子序列,问的是需要到达公共子序列所需要的步数:
即 word1.length - LCS.length + word2.length - LCS.length
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| class Solution {
String word1, word2;
int m, n;
int[][] memo;
public int minDistance(String word1, String word2) {
m = word1.length();
n = word2.length();
memo = new int[m][n];
for (int i = 0; i < m; i++) {
Arrays.fill(memo[i], -1);
}
this.word1 = word1;
this.word2 = word2;
int lcsLength = dp(0, 0);
return (m - lcsLength) + (n - lcsLength);
}
private int dp(int i, int j) {
if (i == m || j == n) return 0;
if (memo[i][j] != -1) return memo[i][j];
if (word1.charAt(i) == word2.charAt(j)) {
memo[i][j] = dp(i + 1, j + 1) + 1;
} else {
memo[i][j] = Math.max(
dp(i + 1, j),
dp(i, j + 1)
);
}
return memo[i][j];
}
}
|