闫氏DP分析法
思考方式
拿到问题 可以分成 状态表示 + 状态计算
计算复杂度: 状态数量(多少个状态) X 状态转移方程计算量
状态表示:
状态表示 f(i,j) -> 集合 和 属性
集合指的是 f(i,j) 定义条件下的一种类型集合
属性一般有三种 Max, Min, 方案数

举个例子对于 01 背包问题来说
「f(i,j) 就指 对于前 i 个物品(条件一),满足容量小于等于j的(条件二)取法集合」集合 「集合中价值最大」(属性:Max)
状态计算:
状态怎么被计算出也就是集合是如何划分的,比如当前集合如何划分为若干个更小的子集,子集可以被前面更小的算出来,子集划分一般遵循不重不漏,但是比如如果求最大值最小值,那么就可以重复,但是求方案书就不能够重复
对于01背包问题来说,集合可以被划分为包含i,或者不包含i
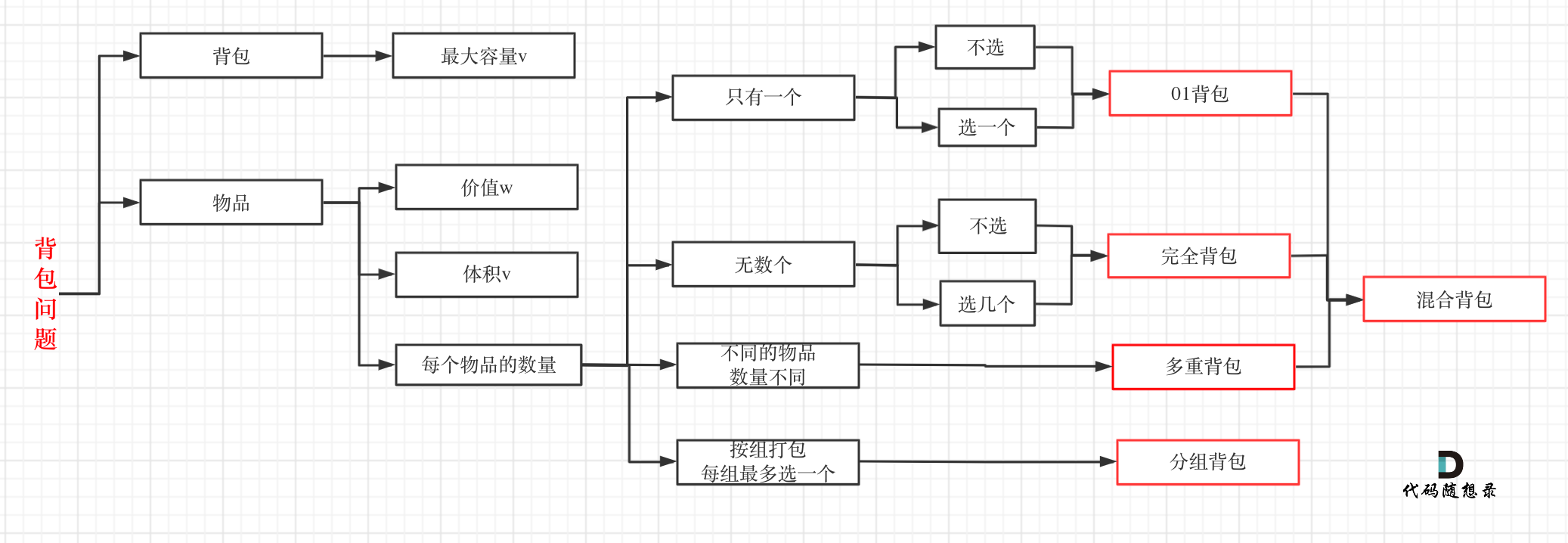
背包问题
背包问题都是说在
N 个物品,每个物品体积Vi, 价值 Wi
容积为 V 的背包
目标是让选择的物品总价值最大求最大值
01 背包:每个物品「至多」选择一次
完全背包:每个物品「无数」次选择
多重背包:每个物品有 「Xi」 个
分组背包:有N组,每个组有若干个物品,每组只能选1个
01背包

一维优化:
能一维优化的原因在于我们当前结果只和i - 1有关,所以在刚要更新的时候当前数组中的值就已经是上一次的值所以无需二维
但是主要讨论下为什么需要倒序,j为什么从m倒退到v[i]
1 | for (int i = 1; i <= n; i++) { |
假设有3件物品,背包的总体积为10
物品 体积 价值
i = 1 4 5
i = 2 5 6
i = 3 6 7
如果 f[0][j] 总共0件物品,所以最大价值为 0, 即 f[0][j] == 0 也是成立的
如果 j 层循环是递增的:
1 | for (int i = 1; i <= n; i++) { |
当还未进入循环时(初始状态):
f[0] = 0; f[1] = 0; f[2] = 0; f[3] = 0; f[4] = 0;
f[5] = 0; f[6] = 0; f[7] = 0; f[8] = 0; f[9] = 0; f[10] = 0;
当进入循环 i == 1 时:
f[4] = max(f[4], f[0] + 5); 即max(0, 5) = 5; 即f[4] = 5;
f[5] = max(f[5], f[1] + 5); 即max(0, 5) = 5; 即f[5] = 5;
f[6] = max(f[6], f[2] + 5); 即max(0, 5) = 5; 即f[6] = 5;
f[7] = max(f[7], f[3] + 5); 即max(0, 5) = 5; 即f[7] = 5;
重点来了!!!
f[8] = max(f[8], f[4] + 5); 即max(0, 5 + 5) = 10; 即f[8] = 10;
这里就已经出错了
因为此时处于 i == 1 这一层,即物品只有一件,不存在单件物品满足价值为10
所以已经出错了。这也是为什么完全背包可以正序,因为它的物品个数是无限
这里是因为在f[8]时候会再一次选用f[4]的结果而f[4]已经用过了不能再用了,(01背包定义)
所以需要从m开始到v[i]以防之前的数被计算过从而导致后面的结果被污染
完全背包

状态优化:
多重背包

二进制优化
(确实不是很懂,主要是为什么分组之后变成选和不选的合理性在哪里?需要做题手推一下)
分组背包

线性dp
线性dp一般指递推的顺序是线性的,比如从左到右。但是定义不重要
Acwing - 889 - 数字三角形
注:图中状态计算有误应该是左上和右上

最长上升子序列
这里的状态计算中指的是当前数的上一个数,比如当前数如果是idx = i 那么上一个是可以是 0(当前数是第一个数,前面一个数不存在), a0, a1, a2, … ai - 1
需要满足 ai - 1 < ai
所以转移方程就是
ai = Max(f[j] + 1), aj < ai, j = 0 … i - 1

最长公共子序列

编辑距离
区间DP
指的是在定义状态时定义了一个区间即状态表示指的是一个区间
石子合并
这里状态是指分割点,因为最后一次一定是将两堆合并成一堆所以f[i, j]就可以由,左边1,2,3,…,k-2,k-1个 右边 k- 1, k-2, k-3,…, 2,1个两堆组成

假设最后一步合并剩下:
左边 [i, k] 右边 [k + 1, j] 两堆
那么这时候的最小代价 Min 属性就是
组成左边一堆石子i, k的合并方式的最小代价 - Min(f[i, k])
组成右边边一堆石子i, k的合并方式的最小代价 - Min(f[k + 1, j])
组成当前堆 [i, j] 堆石子的代价 - 区间[i, j]的代价 (可以使用前缀和公式得出前缀和s[j] - s[i - 1]从而快速获取其代价)
综上:f[i, j] = Min(f[i, k] + f[k + 1, j] + s[j] - s[i - 1]) where k = i ~ j - 1因为这里我们需要保留右边有至少一堆
注:区间dp问题需要注意状态的顺序,看代码之后的总结:
所有的区间dp问题枚举时,第一维通常是枚举区间长度,并且一般 len = 1 时用来初始化,枚举从 len = 2 开始;第二维枚举起点 i (右端点 j 自动获得,j = i + len - 1)
1 | for (int len = 1; len <= n; len++) { // 区间长度 |