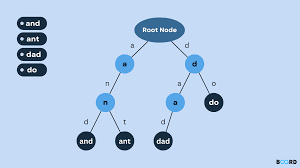
二叉搜索树-BST
基本知识以及操作:
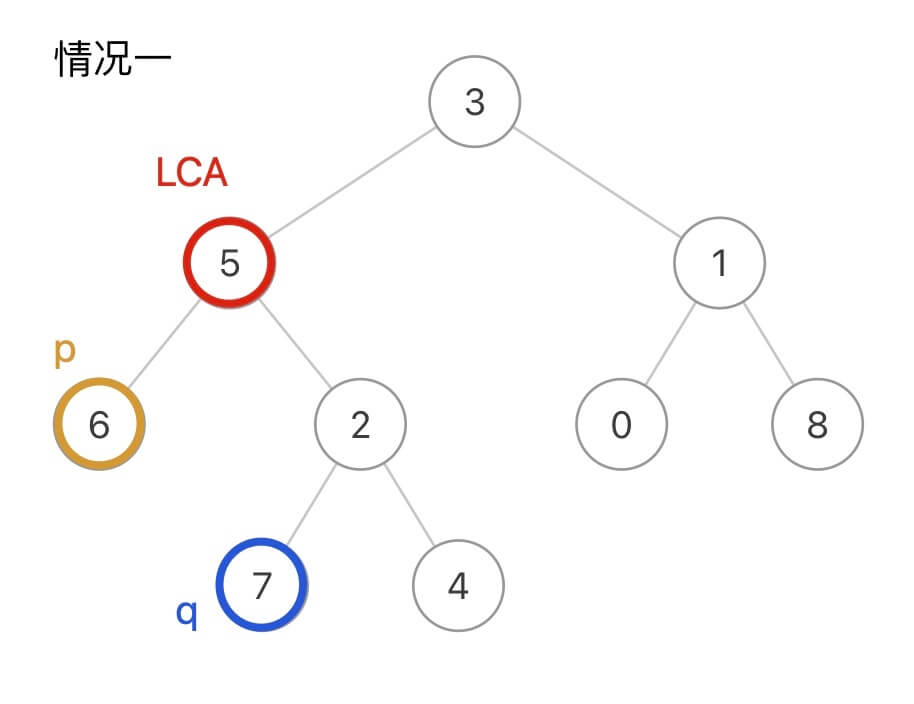
- 提到 BST 就要想到中序遍历:
- BST的中序遍历是有序的
- 性质:
- 左子树所有的值都**(严格)小于**根节点
- 右子树所有的值都**(严格)大于**根节点
- 几乎完美的数据结构,复杂度为树高
- 最左边的叶子结点是最小值,最右边的叶子结点是最大值
那么对于一个数据结构,无非做的事情就是增删查改。
那么就是分成两步:1. 找到要操作的位置 (其实就是查)2. 操作
要找到位置:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| private TreeNode find(TreeNode root, int val) {
if (root == null) return null;
if (root.val == val) {
return root;
} else if (root.val < val) {
return find(root.right, val);
} else if (root.val > val) {
return = find(root.left, val);
}
}
TreeNode searchBST(TreeNode root, int target) {
if (root == null) {
return null;
}
if (root.val > target) {
return searchBST(root.left, target);
}
if (root.val < target) {
return searchBST(root.right, target);
}
return root;
}
|
关于删除操作后的维护:
需要分三种情况:
root 是叶子结点
直接删除叶子结点 即 直接return null 让上一层接收:
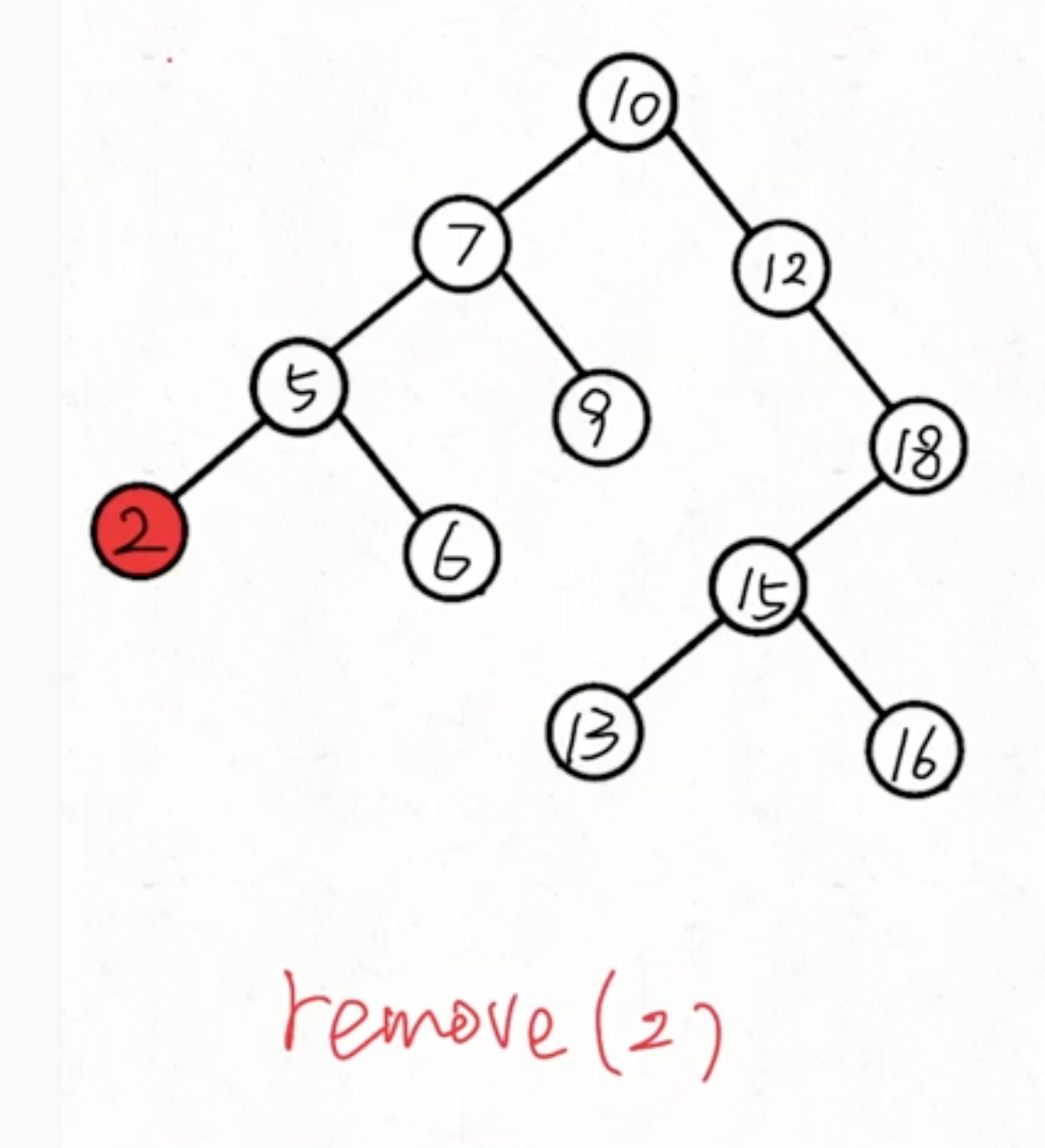
root 左右有一个子节点为空
当左子树不为空:
直接把左子树拼接上去即可,即返回左子树让上一层接收
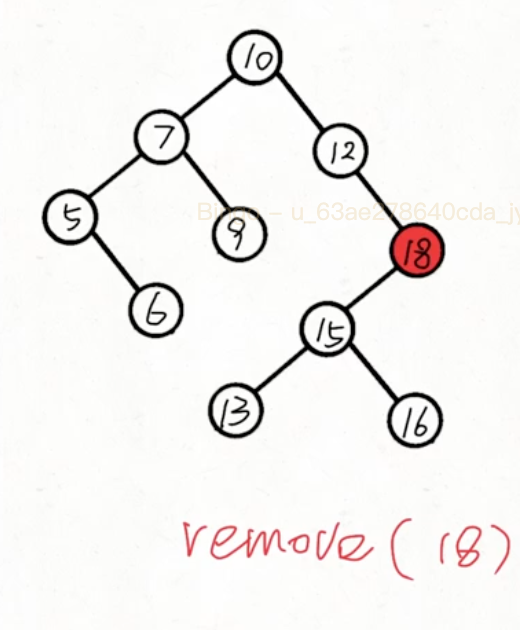
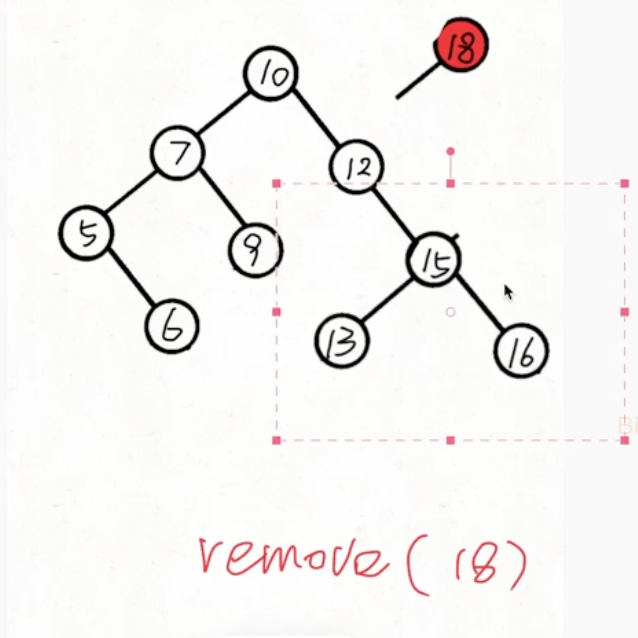
当右子树不为空:
直接把右子树拼接上去即可,即返回右子树让上一层接收
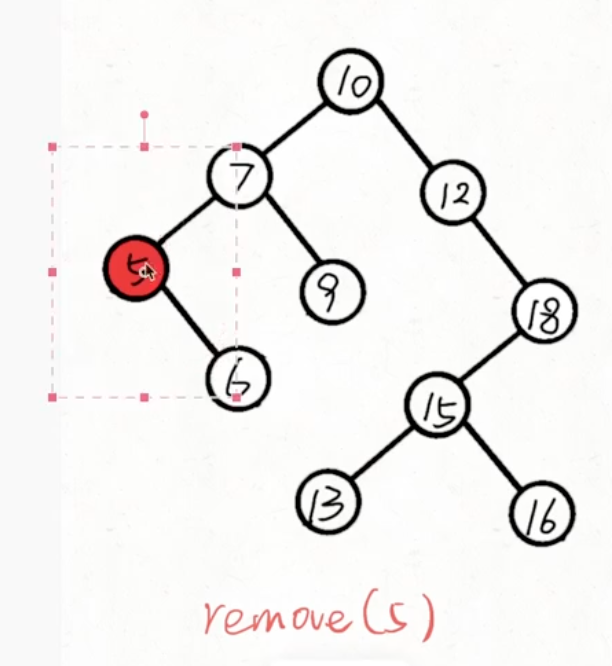
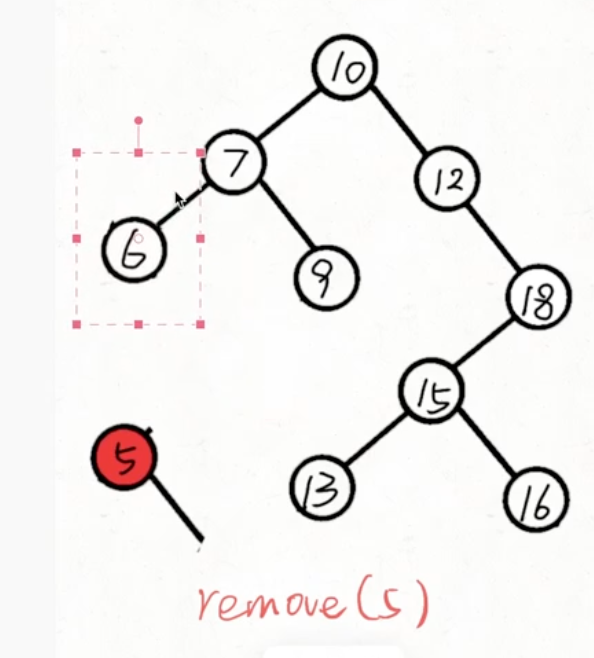
root 左右均不为空
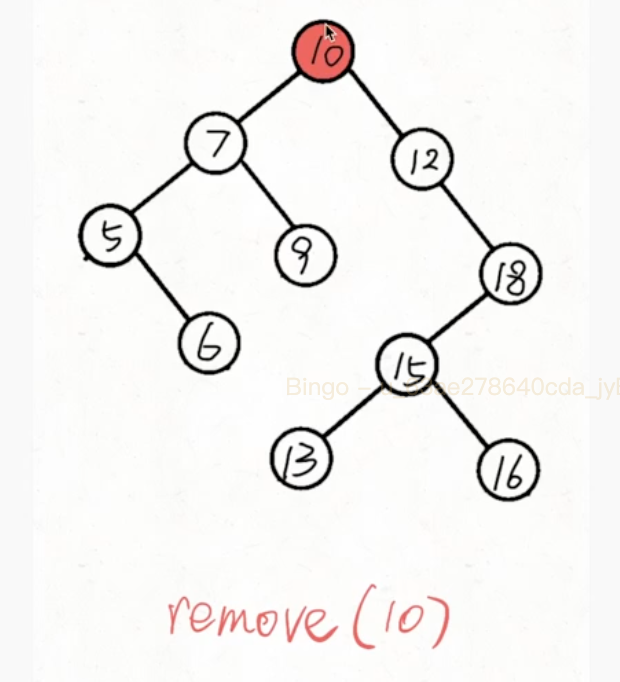
那么情况会变的复杂一些,这是由于要找到能够接替被删除节点位置的节点。这时,我们会有两种选择:
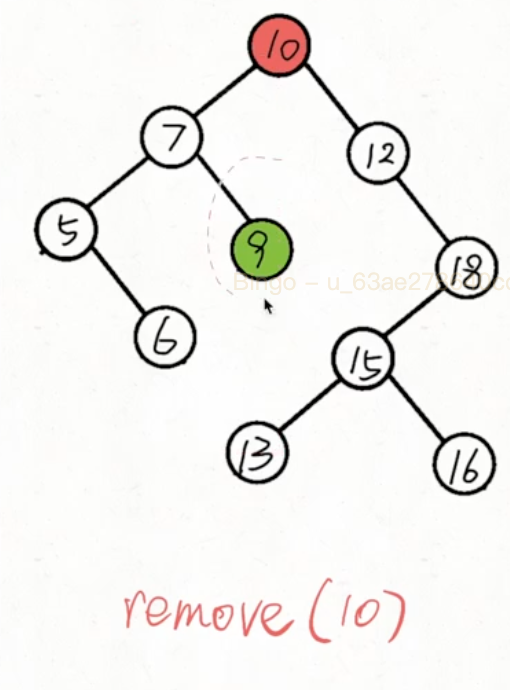
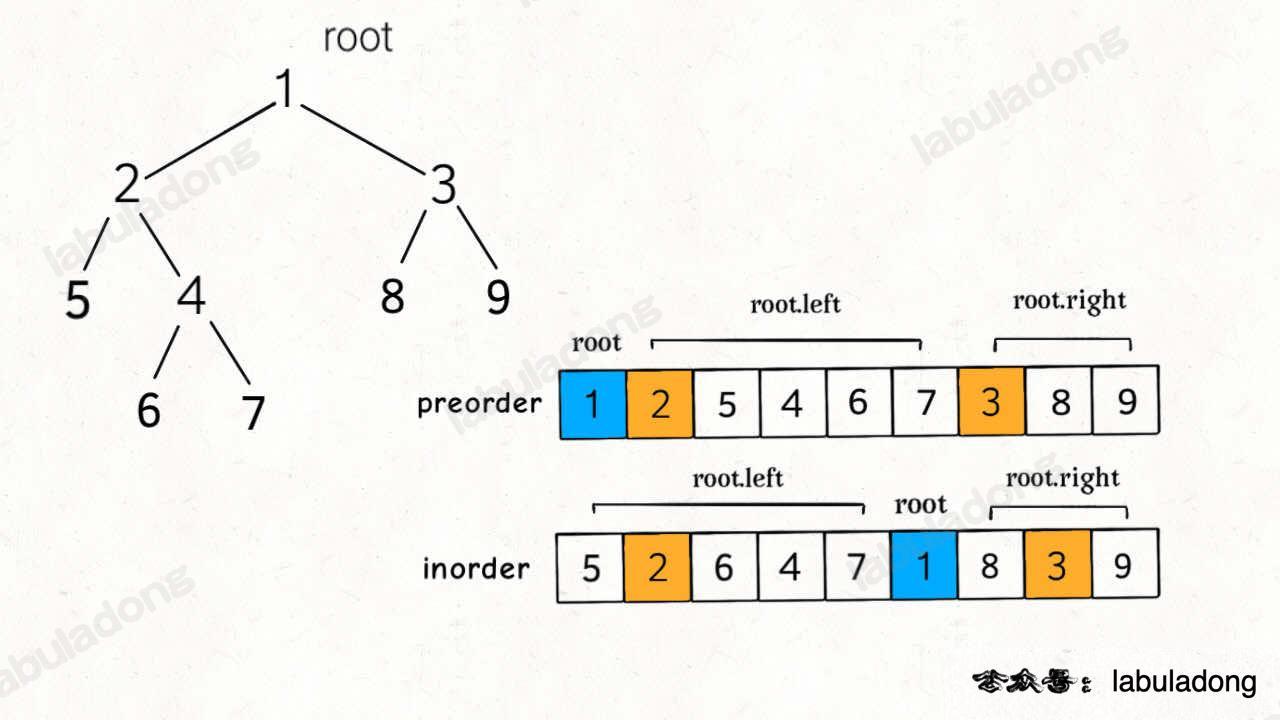
中序遍历而不是前序遍历的原因是:
中序遍历的特性。中序遍历按照“左-根-右”的顺序访问树中的节点。对于二叉搜索树,中序遍历会按照升序的方式访问树中的所有节点。因此,我们可以通过检查在中序遍历过程中每个相邻节点之间的值的大小关系来验证这棵树是否是有效的二叉搜索树。如果遍历的过程中发现某个节点的值小于等于前一个节点的值,那么这棵树就不是一个有效的二叉搜索树。
相反,前序遍历按照“根-左-右”的顺序访问树中的节点,这种顺序无法直接用来验证二叉搜索树的性质。因为前序遍历不保证访问的节点值是按照升序排列的,所以使用前序遍历会使得验证二叉搜索树的过程变得更加复杂。
总之,使用中序遍历是因为它可以直接利用二叉搜索树的性质,按照升序访问树中的节点,从而简化了验证二叉搜索树的过程。
三个方法:
- 使用中序遍历的有序性质 + 辅助数组
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| List<Integer> inOrderResult = new ArrayList<>();
public boolean isValidBST(TreeNode root) {
traverse(root);
for (int i = 0, j = i + 1; j < inOrderResult.size();) {
if (inOrderResult.get(j) <= inOrderResult.get(i)) {
return false;
}
i++;
j++;
}
return true;
}
private void traverse(TreeNode root) {
if (root == null) return;
traverse(root.left);
inOrderResult.add(root.val);
traverse(root.right);
}
|
- 借用一个非常小的值 继续使用中序遍历 PS:这里使用long minValue的原因是有可能存在int的最小值从而使得无法正确判断当左叶子结点特别小(Int MinValue)的情况。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| long longMin = Long.MIN_VALUE;
public boolean isValidBST(TreeNode root) {
return traverse(root);
}
private boolean traverse(TreeNode root) {
if (root == null) return true;
boolean left = traverse(root.left);
if (root.val <= longMin) {
return false;
}
longMin = root.val;
boolean right = traverse(root.right);
return left && right;
}
|
- 双指针,注意previousNode应该作为全局变量从而每一个更新都能被正确更新。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| TreeNode previousNode = null;
public boolean isValidBST(TreeNode root) {
return traverse(root);
}
private boolean traverse(TreeNode root) {
if (root == null) return true;
boolean left = traverse(root.left);
if (previousNode != null && previousNode.val >= root.val) {
return false;
}
previousNode = root;
boolean right = traverse(root.right);
return left && right;
}
|
作为参数传递的方法:
之前previousNode没有正确地更新的原因是:Java中的参数传递采用的是值传递(pass-by-value)。虽然Java中的对象是引用类型,但实际上传递的是引用的副本。因此,在函数traverse内部修改previousNode的值(例如previousNode = root;)不会影响到调用方的previousNode。
要解决这个问题,可以将previousNode的引用包装在一个可变的容器类中,例如一个单元素的数组。这样,在递归调用中,previousNode的更新将会影响到调用方。以下是修改后的代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| TreeNode[] previousNode = new TreeNode[1];
public boolean isValidBST(TreeNode root) {
return traverse(root, previousNode);
}
private boolean traverse(TreeNode root, TreeNode[] previousNode) {
if (root == null) return true;
boolean left = traverse(root.left, previousNode);
if (previousNode[0] != null && previousNode[0].val >= root.val) {
return false;
}
previousNode[0] = root;
boolean right = traverse(root.right, previousNode);
return left && right;
}
|
插入操作和二叉树的构造类型题非常类似详情见 二叉树之构造类问题
不难,详情看代码注释即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| public TreeNode insertIntoBST(TreeNode root, int val) {
return insert(root, val);
}
private TreeNode insert(TreeNode root, int val) {
if (root == null) return new TreeNode(val);
if (root.val < val) {
root.right = insert(root.right, val);
} else if (root.val > val) {
root.left = insert(root.left, val);
}
return root;
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
| public TreeNode deleteNode(TreeNode root, int key) {
return delete(root, key);
}
private TreeNode delete(TreeNode root, int key) {
if (root == null) return null;
if (root.val > key) {
root.left = delete(root.left, key);
} else if (root.val < key) {
root.right = delete(root.right, key);
} else {
if (root.left == null) {
return root.right;
} else if (root.right == null) {
return root.left;
} else {
TreeNode leftTreeMaxNode = findLeftTreeMaxNode(root.left);
root.left = removeLeftTreeMaxNode(root.left);
leftTreeMaxNode.left = root.left;
leftTreeMaxNode.right = root.right;
root = leftTreeMaxNode;
}
}
return root;
}
private TreeNode findLeftTreeMaxNode(TreeNode root) {
while (root.right != null) {
root = root.right;
}
return root;
}
private TreeNode removeLeftTreeMaxNode(TreeNode root) {
if (root.right == null) {
return root.left;
}
root.right = removeLeftTreeMaxNode(root.right);
return root;
}
|
利用BST的性质 递归的处理左树和右树
1、**root.val < lo,这种情况下 root 节点本身和 root 的左子树全都是小于 lo 的,都需要被剪掉**。
2、**root.val > hi,这种情况下 root 节点本身和 root 的右子树全都是大于 hi 的,都需要被剪掉**。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| class Solution {
public TreeNode trimBST(TreeNode root, int low, int high) {
TreeNode rootTrimmed = buildTree(root, low, high);
return rootTrimmed;
}
private TreeNode buildTree(TreeNode root, int low, int high) {
if (root == null) return null;
if (root.val < low) {
return buildTree(root.right, low, high);
}
if (root.val > high) {
return buildTree(root.left, low, high);
}
root.left = buildTree(root.left, low, high);
root.right = buildTree(root.right, low, high);
return root;
}
}
|
和利用前序和后序数组构造二叉树题目类型非常相似,确定好左右区间,确定好根节点即可:
关于 前序和后序数组构造二叉树题目 见 二叉树之构造类问题
1
2
3
4
5
6
7
8
9
10
11
12
13
| class Solution {
public TreeNode sortedArrayToBST(int[] nums) {
return buildTree(nums, 0, nums.length - 1);
}
private TreeNode buildTree(int[] nums, int left, int right) {
if (left > right) return null;
int mid = (left + right) >> 1;
TreeNode root = new TreeNode(nums[mid]);
root.left = buildTree(nums, left, mid - 1);
root.right = buildTree(nums, mid + 1, right);
return root;
}
}
|
利用BST性质,降序输出,这个也是利用了双指针的性质:
可以想象成一个数组:
6 7 8
需要一个 累加 数组,此时用双指针 pre cur 指向 7 8
那么问题就好解决了,同理,是用双指针:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| class Solution {
int pre = 0;
public TreeNode convertBST(TreeNode root) {
traverse(root);
return root;
}
private void traverse(TreeNode root) {
if (root == null) return;
traverse(root.right);
root.val += pre;
pre = root.val;
traverse(root.left);
return;
}
}
|
第二种解法:使用sum作为外部变量
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| class Solution {
int sum = 0;
public TreeNode convertBST(TreeNode root) {
traverse(root);
return root;
}
private void traverse(TreeNode root) {
if (root == null) return;
traverse(root.right);
sum += root.val;
root.val = sum;
traverse(root.left);
return;
}
}
|