代码随想录

数组

例题

704.二分查找
题目建议： 大家能把 704 掌握就可以，35.搜索插入位置 和 34. 在排序数组中查找元素的第一个和最后一个位置 ，如果有时间就去看一下，没时间可以先不看，二刷的时候在看。
先把 704写熟练，要熟悉 根据 左闭右开，左闭右闭 两种区间规则 写出来的二分法。

见 二分查找 专题

27.移除元素
题目建议： 暴力的解法，可以锻炼一下我们的代码实现能力，建议先把暴力写法写一遍。 双指针法 是本题的精髓，今日需要掌握，至于拓展题目可以先不看。

见 双指针 专题

977.有序数组的平方
题目建议： 本题关键在于理解双指针思想

见 双指针 专题

209.长度最小的子数组
题目建议： 本题关键在于理解滑动窗口，这个滑动窗口看文字讲解 还挺难理解的，建议大家先看视频讲解。 拓展题目可以先不做。

见 双指针 专题

59.螺旋矩阵II
题目建议： 本题关键还是在转圈的逻辑，在二分搜索中提到的区间定义，在这里又用上了。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
public int[][] generateMatrix(int n) {
    // 此题的关键点在于循环不变量
    // 即 每次循环中都要遵循一个准则，
    // 如二分法中的 左闭右闭 或 左闭右开 性质的定义
    // 我们规定左闭右开，即每一行/列的最后一个值交由下一次循环处理：
    int startX = 0, startY = 0;
    int i = 0, j = 0;
    int offset = 1;
    int count = 1;
    int[][] res = new int[n][n];
    int circleCount = n / 2;
    while (circleCount > 0) {
        // 处理上边的行：（左到右）
        for (j = startY; j < n - offset; j++) {
            res[startX][j] = count++;
        }
        // 处理右边的列：（上到下）
        for (i = startX; i < n - offset; i++) {
            res[i][j] = count++;
        }
        // 处理下边的行：（右到左）
        for (; j > startY; j--) {
            res[i][j] = count++;
        }
        // 处理左边的列：（下到上）
        for (; i > startX; i--) {
            res[i][j] = count++;
        }
        startX++;
        startY++;
        offset++;
        circleCount--;
    }
    if (n % 2 != 0) {
        res[startX][startY] = count;
    }
    return res;

}

链表

基本知识：

其是一种通过指针串联在一起的 线性 数据结构，每一个节点都包含：数据域 和 指针域，最后一个节点的指针域指向null, aka 空指针。

常见的包含三种类型：单链表（上述），双链表，循环链表：

单链表：

上述，它的指针域只能指向节点的下一个节点。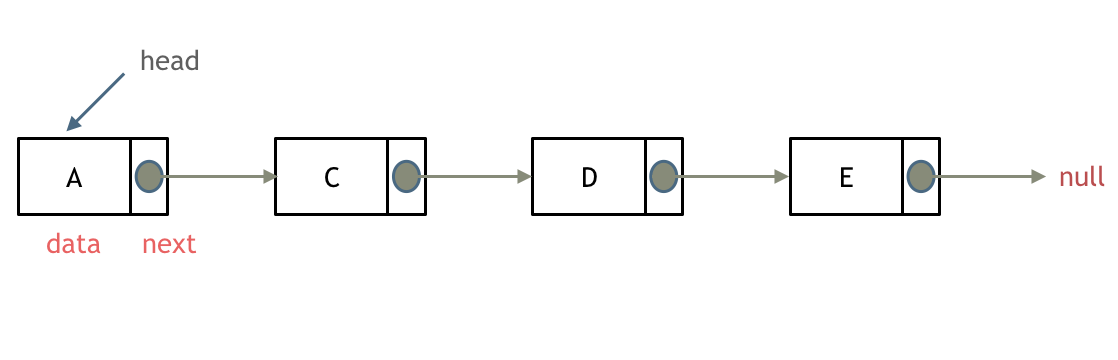
单链表

双链表：

每一个节点有两个指针域，一个指向下一个节点，一个指向上一个节点。因此双链表可以向前以及向后查。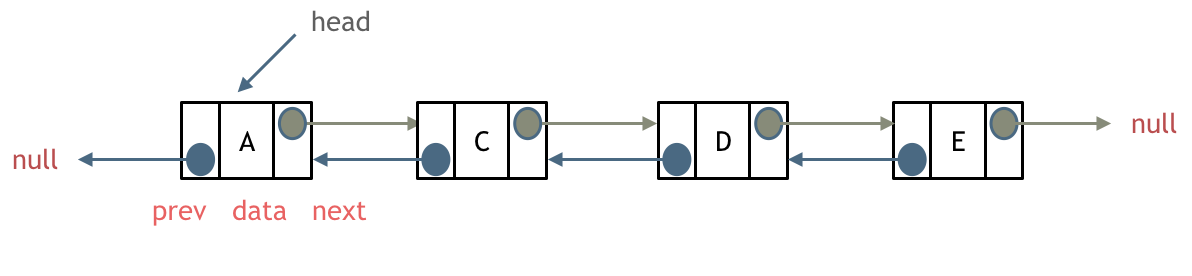
双链表

循环链表

链表首尾相连，可以用来解决约瑟夫环的问题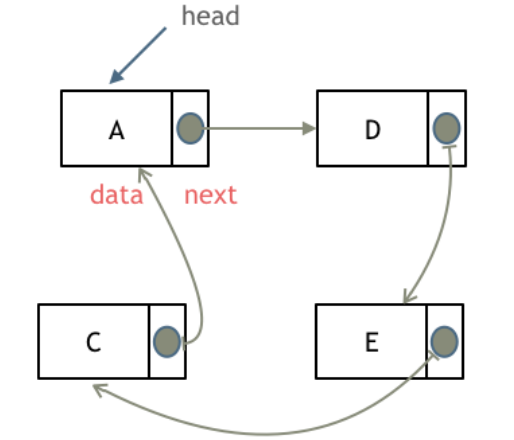
循环链表

存储方式：

  1. 不是连续分布，instead, 散乱分布
  2. 通过指针链接内存中的各个节点

定义：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
public class ListNode {
    // 结点的值
    int val;

    // 下一个结点
    ListNode next;

    // 节点的构造函数(无参)
    public ListNode() {
    }

    // 节点的构造函数(有一个参数)
    public ListNode(int val) {
        this.val = val;
    }

    // 节点的构造函数(有两个参数)
    public ListNode(int val, ListNode next) {
        this.val = val;
        this.next = next;
    }
}

操作

删除节点：
next指向下一个即可

添加节点：取消原本的next，指向新的节点，新的节点指向下一个节点。

可以看出链表的增添和删除都是O(1)操作，也不会影响到其他节点。但是要注意，要是删除第五个节点，需要从头节点查找到第四个节点通过next指针进行删除操作，查找的时间复杂度是O(n)。

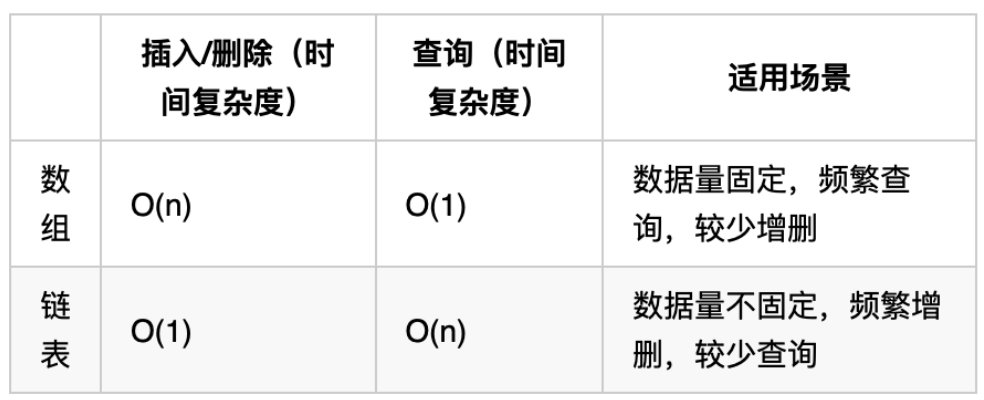
链表性能分析

总结

数组在定义的时候，长度就是固定的，如果想改动数组的长度，就需要重新定义一个新的数组。

链表的长度可以是不固定的，并且可以动态增删， 适合数据量不固定，频繁增删，较少查询的场景。

例题：

例题详解见 链表

● 203.移除链表元素
● 707.设计链表
● 206.反转链表
● 24. 两两交换链表中的节点
● 19.删除链表的倒数第N个节点
● 面试题 02.07. 链表相交
● 142.环形链表II

哈希表

基本知识：

即 Hash Table, 又称散列表。
哈希表是根据关键码的值而直接进行防卫的数据结构。e.g.数组就是哈希表的一个非常好的应用因为可以通过下标来返回对应值。
主要解决的问题： 快速判断一个元素是否出现在集合里。
值 -> 哈希表 的 映射 即为Hash Function aka 哈希函数 \

哈希函数

哈希函数
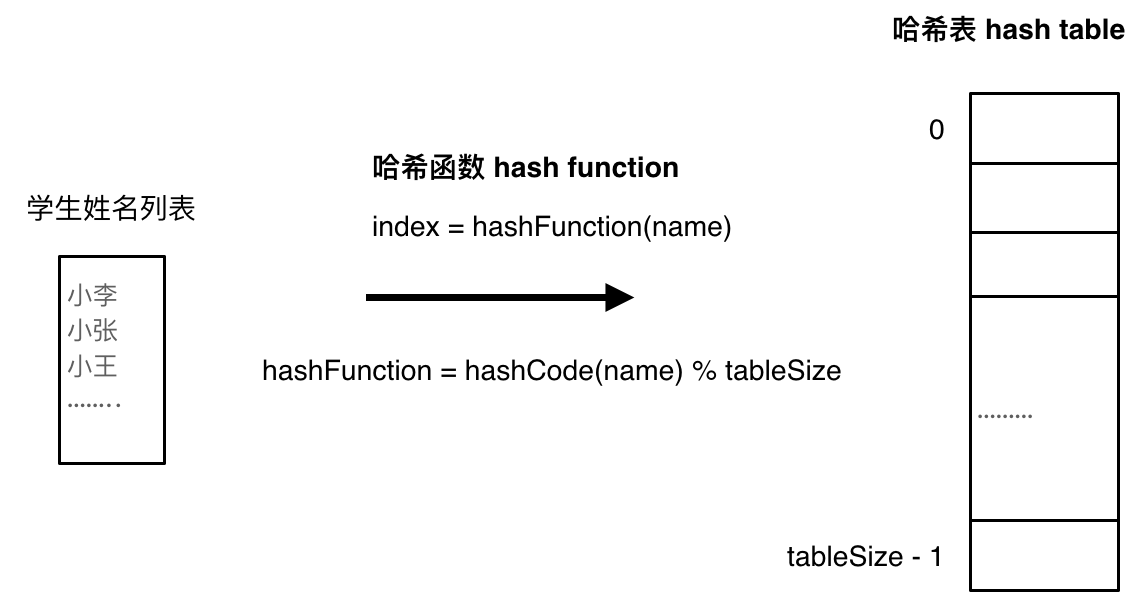
把学生姓名映射到了哈希表存储的函数过程。通过hashCode把名字转化为数值，一般hashcode是通过特定编码方式，可以将其他数据格式转化为不同的数值，这样就把学生名字映射为哈希表上的索引数字了。

问题1: 如果hashCode得到的数值大于 哈希表的大小了，也就是大于tableSize了 怎么办？

此时为了保证映射出来的索引数值都落在哈希表上，我们会在再次对数值做一个取模的操作，就要我们就保证了学生姓名一定可以映射到哈希表上了。

问题2: 如果学生的数量大于哈希表的大小，此时就算哈希函数计算的再均匀，也避免不了会有几位学生的名字同时映射到哈希表 同一个索引下标的位置。

即哈希碰撞的处理问题

哈希碰撞, Hash Collisions：

两个值映射到了同一个位置即为Hash Collisions

哈希碰撞
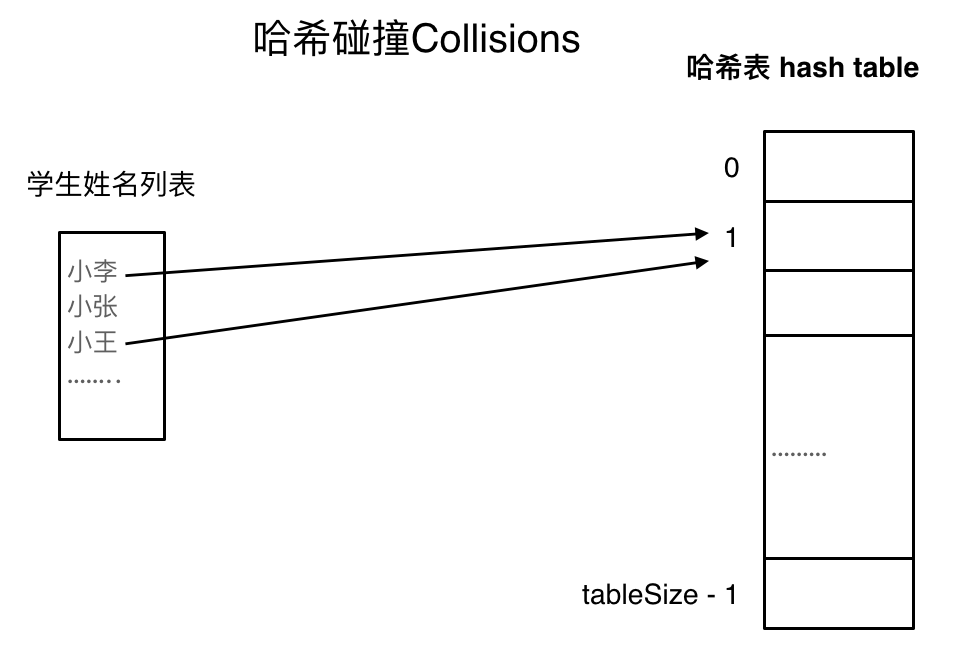
解决方法：

  1. 拉链法
  2. 线性探测法
拉链法

从冲突的位置拉一条链表出来：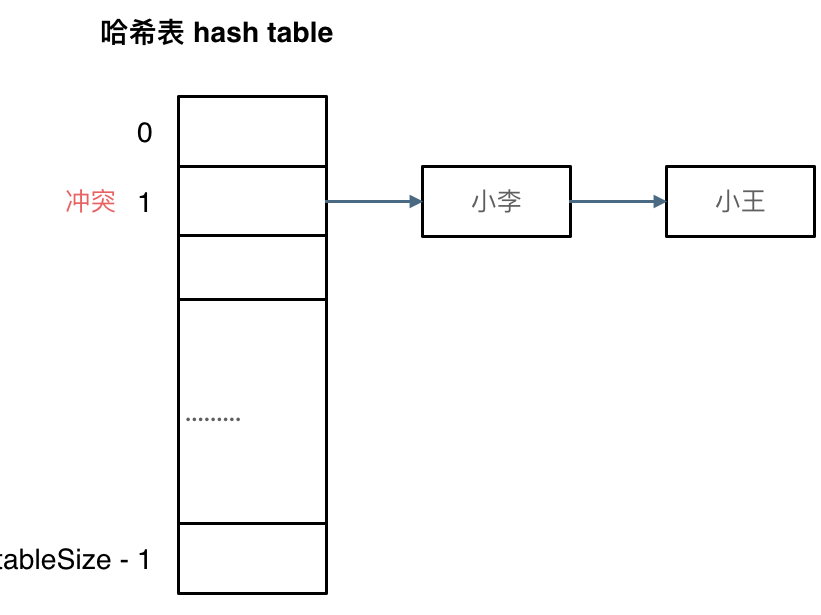
拉链法
需要注意的是链表上的查询需要一个一个查，因此大小很重要。

线性探测法

要求 hash table 的大小 一定 要大于 data size 因为需要依赖哈希表中的空位来解决碰撞问题。线性探测法要把冲突的元素放在下一个 空闲的 位置

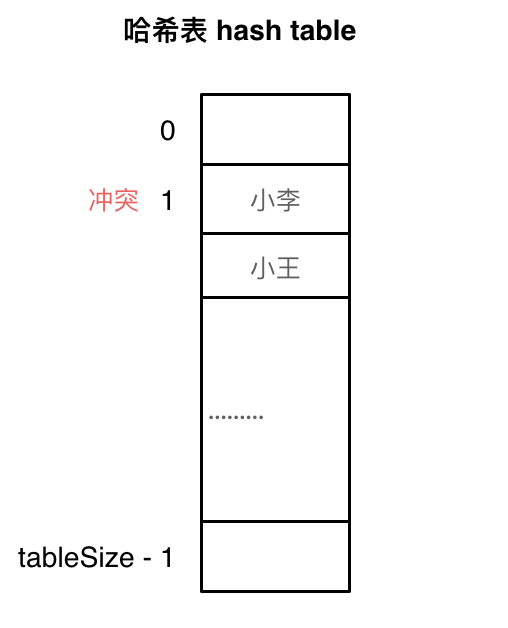
线性冲突法

图中小王需要放到小李的下面的位置。

常见的哈希结构：

一般会有以下三种结构：

  1. 数组
  2. hashset
  3. hashmap
数据结构 底层实现 是否有序 数值是否可以重复 能否更改数值 查询效率 增删效率
HashMap 哈希表（数组 + 链表/红黑树） 无序 键不可重复，值可重复 可以 O(1) ~ O(n) O(1) ~ O(n)
HashSet 基于HashMap实现 无序 不可重复 间接支持 O(1) ~ O(n) O(1) ~ O(n)
TreeMap 红黑树 有序 键不可重复，值可重复 可以 O(log n) O(log n)
HashMap HashSet TreeMap
底层实现：哈希表（数组 + 链表/红黑树） 基于HashMap实现 红黑树
是否有序：无序 无序 有序
数值是否可以重复：键不可重复，值可重复 不可重复 键不可重复，值可重复
能否更改数值：可以 通过put()方法更新键对应的值。 间接支持 可以通过put()方法更新键对应的值
查询效率：O(1) ~ O(n) O(1) ~ O(n) O(log n) 由于红黑树是平衡的
增删效率：O(1) ~ O(n) O(1) ~ O(n) O(log n) 由于红黑树是平衡的
  1. TreeMap

底层实现：基于红黑树实现，红黑树是一种自平衡的二叉搜索树。是否有序：保证有序。TreeMap中的元素按照键（Key）的自然顺序或者提供的比较器（Comparator）进行排序。数值是否可以重复：键（Key）不可重复，值（Value）可重复。能否更改数值：可以更改数值。通过put()方法更新键对应的值。查询效率：时间复杂度为O(log n)，其中n为元素数量。由于红黑树是平衡的，查询效率相对较高。增删效率：时间复杂度为O(log n)，其中n为元素数量。由于红黑树具有自平衡特性，增删操作效率相对较高。

例题

例题详解见 哈希表

● 242.有效的字母异位词

● 349. 两个数组的交集

● 202. 快乐数

● 1. 两数之和

● 454.四数相加II

● 383. 赎金信

● 15. 三数之和

● 18. 四数之和

总结

  1. 当我们遇到了要快速判断一个元素是否出现集合里的时候，就要考虑哈希法。其本质是通过 通过空间换了时间
  2. 经典题目：
    1. 数组作为哈希表：eg: int[] = new int[26];
      1. 在242.有效的字母异位词中，我们提到了数组就是简单的哈希表，但是数组的大小是受限的！这道题目包含小写字母，那么使用数组来做哈希最合适不过。在383.赎金信中同样要求只有小写字母，那么就给我们浓浓的暗示，用数组！和242.有效的字母异位词很像，242.有效的字母异位词是求 字符串a 和 字符串b 是否可以相互组成，在383.赎金信中是求字符串a能否组成字符串b，而不用管字符串b 能不能组成字符串a。
    2. Set作为哈希表：
      1. 在349. 两个数组的交集 (opens new window)中我们给出了什么时候用数组就不行了，需要用set。这道题目没有限制数值的大小，就无法使用数组来做哈希表了。
      2. 主要因为如下两点：
        1. 数组的大小是有限的，受到系统栈空间（不是数据结构的栈）的限制。
        2. 如果数组空间够大，但哈希值比较少、特别分散、跨度非常大，使用数组就造成空间的极大浪费。
    3. Map本身作为哈希表：
      1. e g: 两数之和
      2. 数组的大小是受限制的，而且如果元素很少，而哈希值太大会造成内存空间的浪费。
      3. set是一个集合，里面放的元素只能是一个key，而两数之和这道题目，不仅要判断y是否存在而且还要记录y的下标位置，因为要返回x 和 y的下标。所以set 也不能用。

字符串

总结

  1. 字符串是字符组成的有限序列
  2. 使用方法：
    1. 双指针：
      1. 344.反转字符串
      2. 剑指Offer 05.替换空格
    2. 反转
      1. 例题： 541. 反转字符串II
      2. 例题：151.翻转字符串里的单词
    3. KMP

例题

例题详解见 字符串

● 344.反转字符串

● 541. 反转字符串II

● 剑指Offer 05.替换空格

● 151.翻转字符串里的单词

● 剑指Offer58-II.左旋转字符串

● 28. 实现 strStr()

● 459.重复的子字符串

队列 (Queue) and 栈 (Stack)

例题详解见 队列和栈

  1. 队列先进先出 FIFO 栈先进后出 FILO

Java

在 Java 中，栈（Stack）和队列（Queue）是两种常用的数据结构。它们可以通过 Java 集合框架中的类来实现。

栈（Stack）实现方法：

Java 有一个名为 Stack 的类。但是，由于 Stack 类被认为是过时的，不推荐使用。相反，我们可以使用 Deque（双端队列）来实现栈。以下是使用 Deque 实现栈的方法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import java.util.Deque;
import java.util.LinkedList;

public class StackExample {
    public static void main(String[] args) {
        Deque<Integer> stack = new LinkedList<>();

        // 入栈
        stack.push(1);
        stack.push(2);
        stack.push(3);

        // 出栈
        System.out.println(stack.pop());
        System.out.println(stack.pop());
    }
}

栈的底层实现是通过数组或链表。在这个例子中，我们使用了 LinkedList（链表）作为底层实现。栈的主要操作（push 和 pop）的时间复杂度是 O(1)。

队列（Queue）实现方法：

Java 提供了 Queue 接口来实现队列。以下是使用 LinkedList 实现队列的方法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import java.util.LinkedList;
import java.util.Queue;

public class QueueExample {
    public static void main(String[] args) {
        Queue<Integer> queue = new LinkedList<>();

        // 入队
        queue.offer(1);
        queue.offer(2);
        queue.offer(3);

        // 出队
        System.out.println(queue.poll());
        System.out.println(queue.poll());
    }
}

队列的底层实现可以是数组或链表。在这个例子中，我们使用了 LinkedList（链表）作为底层实现。队列的主要操作（offer 和 poll）的时间复杂度是 O(1)。

注意：虽然在上面的例子中，我们使用 LinkedList 作为底层实现，但实际上还有其他实现方式，如 ArrayDeque（基于数组的双端队列），它在某些情况下可能比 LinkedList 更高效。另外，Java 还提供了 PriorityQueue（优先队列），其底层实现是基于二叉堆的数据结构，用于实现具有优先级的队列。

优先队列 (Priority Queue):

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
import java.util.Comparator;
import java.util.PriorityQueue;

public class PriorityQueueExample {
    public static void main(String[] args) {
        // 创建一个整数优先队列
        PriorityQueue<Integer> intQueue = new PriorityQueue<>();

        // 将整数添加到优先队列
        intQueue.offer(5);
        intQueue.offer(2);
        intQueue.offer(8);
        intQueue.offer(1);

        // 将整数从优先队列中删除并打印（默认为自然顺序，即升序）
        while (!intQueue.isEmpty()) {
            System.out.println(intQueue.poll());
        }

        // 创建一个字符串优先队列，使用自定义的 Comparator 对象
        PriorityQueue<String> stringQueue = new PriorityQueue<>(new StringLengthComparator());

        // 将字符串添加到优先队列
        stringQueue.offer("apple");
        stringQueue.offer("banana");
        stringQueue.offer("cherry");
        stringQueue.offer("date");

        // 将字符串从优先队列中删除并打印（根据字符串长度排序）
        while (!stringQueue.isEmpty()) {
            System.out.println(stringQueue.poll());
        }
    }

    // 自定义的 Comparator 类，按字符串长度进行排序
    static class StringLengthComparator implements Comparator<String> {
        @Override
        public int compare(String s1, String s2) {
            return s1.length() - s2.length();
        }
    }
}

Comparator in one line:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
import java.util.Comparator;
import java.util.PriorityQueue;

public class PriorityQueueExample {
    public static void main(String[] args) {
        // 创建一个字符串优先队列，使用自定义的 Comparator 对象
        PriorityQueue<String> stringQueue = new PriorityQueue<>(new Comparator<String>() {
            @Override
            public int compare(String s1, String s2) {
                return s1.length() - s2.length();
            }
        });

        // 将字符串添加到优先队列
        stringQueue.offer("apple");
        stringQueue.offer("banana");
        stringQueue.offer("cherry");
        stringQueue.offer("date");

        // 将字符串从优先队列中删除并打印（根据字符串长度排序）
        while (!stringQueue.isEmpty()) {
            System.out.println(stringQueue.poll());
        }
    }
}

例题

例题详解见 队列和栈

● 232.用栈实现队列

● 225. 用队列实现栈

● 20. 有效的括号

● 1047. 删除字符串中的所有相邻重复项

● 150. 逆波兰表达式求值

● 239. 滑动窗口最大值

● 347.前 K 个高频元素

总结

  1. 225.用队列实现栈：一个队列在模拟栈弹出元素的时候只要将队列头部的元素（除了最后一个元素外） 重新添加到队列尾部，此时在去弹出元素就是栈的顺序了。
栈的应用
  1. 括号匹配（有效的括号）, 表达式（逆波兰表达式求值），字符串相邻元素去重（删除字符串中的所有相邻重复项）都是使用栈解决的经典问题其核心是匹配问题
队列的应用
  1. 滑动窗口最大值问题中，队列没有必要维护窗口里的所有元素，只需要维护有可能成为窗口里最大值的元素就可以了，同时保证队列里的元素数值是由大到小的。
  2. 单调队列 ≠ 优先队列
  3. 单调队列不是一成不变的，而是不同场景不同写法，总之要保证队列里单调递减或递增的原则，所以叫做单调队列。
优先队列

一个披着队列外衣的堆，优先队列对外接口只是从队头取元素，从队尾添加元素，再无其他取元素的方式，看起来就是一个队列。

堆是一棵完全二叉树，树中每个结点的值都不小于（或不大于）其左右孩子的值。 如果父亲结点是大于等于左右孩子就是大顶堆，小于等于左右孩子就是小顶堆。

前 K 个高频元素 用到了优先队列

二叉树

二叉树基本知识

二叉树种类

主要有两种：满二叉树以及完全二叉树

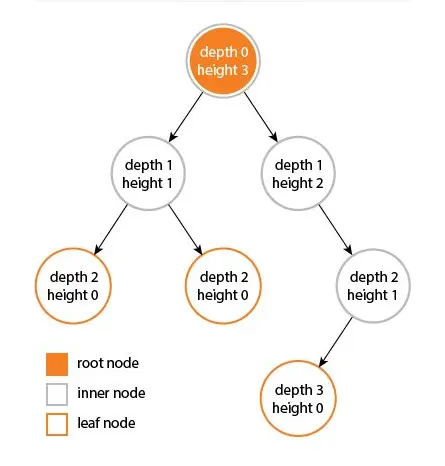
节点的高度：节点到最远叶子节点的最长路径上边的数量。叶子节点高度为0。
节点的深度：节点到根节点的路径上边的数量。所有根节点深度为0。
树的高度：树的高度等于根节点的高度，等于最远叶子节点的深度。
树的深度：树的深度等于树的高度。
树的宽度：两个最长路径的叶子节点之间节点数。

二叉树名词

满二叉树

定义：除最后一层无任何子节点外，每一层上的所有结点都有两个子结点（最后一层上的无子结点的结点为 叶子结点 ）。也可以这样理解，除叶子结点外的所有结点均有两个子结点。节点数达到最大值。所有叶子结点必须在同一层上.

例子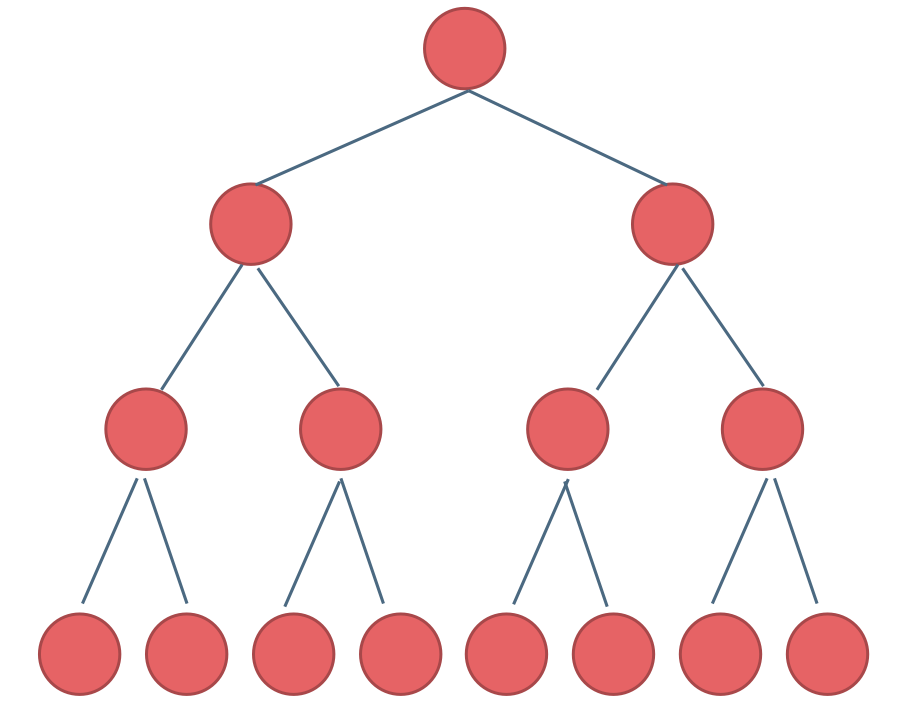：满二叉树

深度为k，有 2 ^ (k-1) 个节点的二叉树

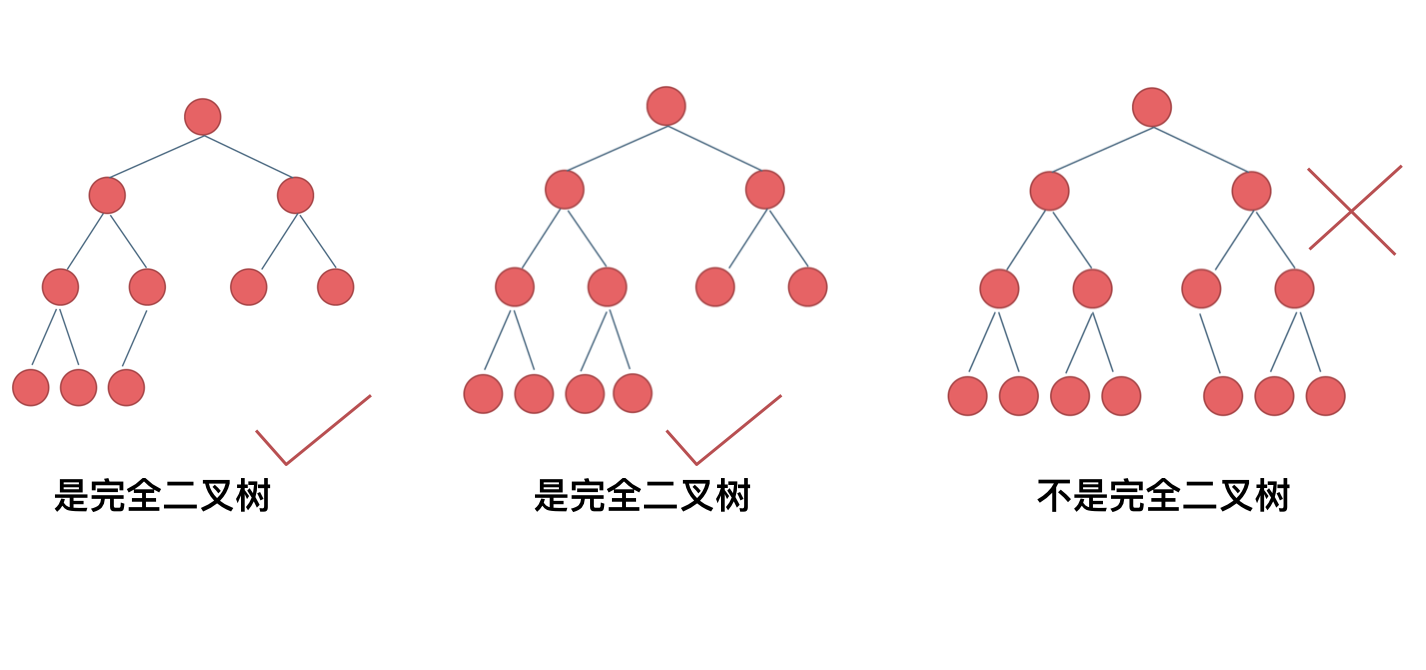
完全二叉树

除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2^(h-1) 个节点。

完全二叉树

ps: 优先队列 用到了 堆 而堆就是一个完全二叉树但保证了父子节点的顺序关系

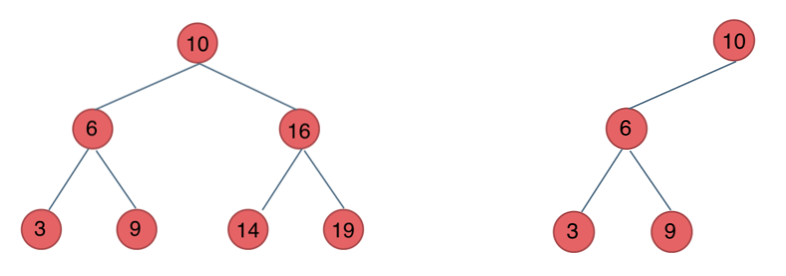
二叉搜索树

二叉搜索树，有值，且其是一个有序树。对节点没有要求，对顺序有要求

有以下三个特点：

  • 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
  • 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
  • 它的左、右子树也分别为二叉排序树

二叉搜索树

平衡二叉搜索树

平衡二叉查找树：简称平衡二叉树

特点：任一节点对应的两棵子树的最大高度差为1，因此它也被称为高度平衡树。查找、插入和删除在平均和最坏情况下的时间复杂度都是 O(logN)

总结：

  1. 可以是空树。
  2. 假如不是空树，任何一个结点的左子树与右子树都是平衡二叉树，并且高度之差的绝对值不超过 1。

平衡二叉搜索树

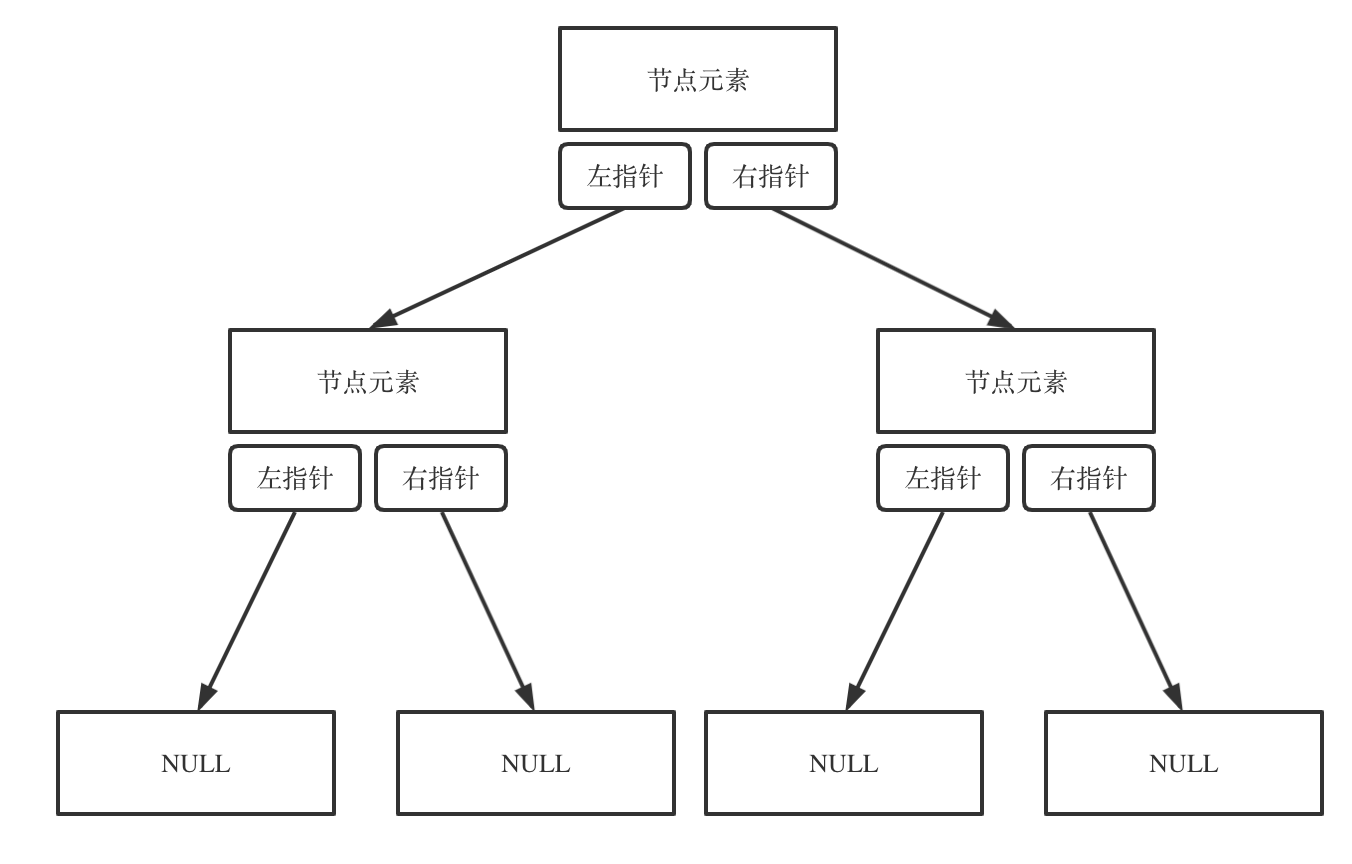
二叉树的存储方式

两种：

  1. 用指针的链式存储

链式存储

  1. 用数组的顺序存储

顺序存储

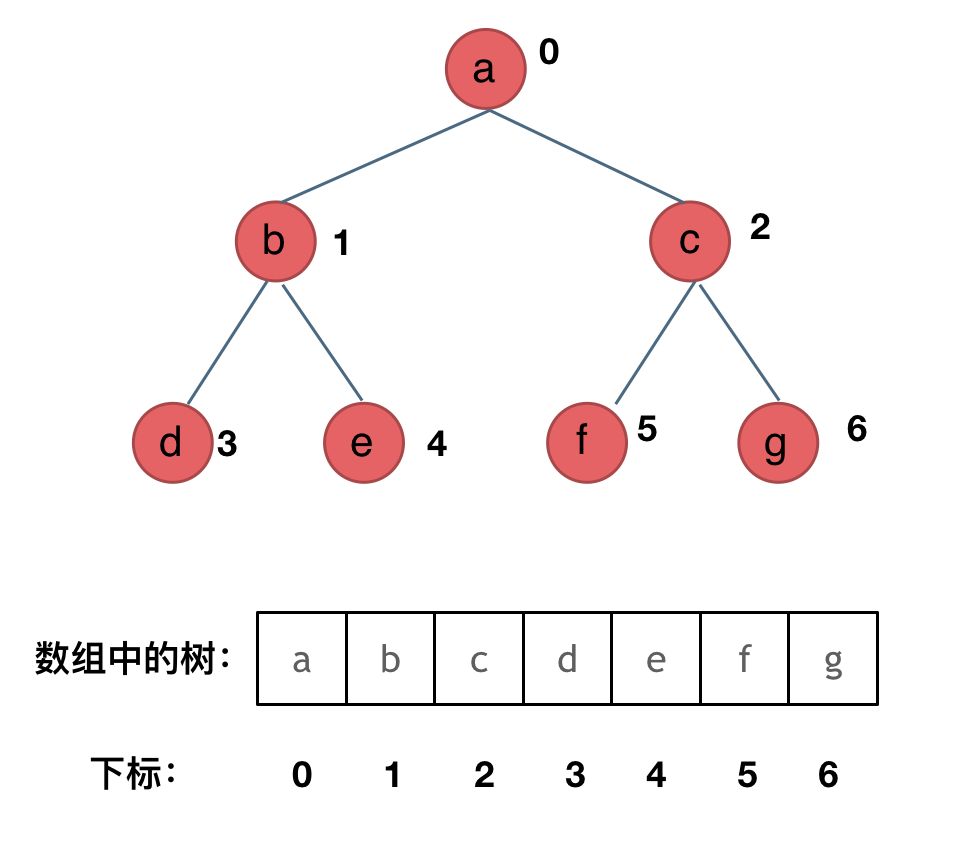
如果父节点的数组下标是 i，那么它的左孩子就是 i * 2 + 1，右孩子就是 i * 2 + 2。

二叉树的遍历

二叉树主要有两种遍历方式：

  1. 深度优先遍历：先往深走，遇到叶子节点再往回走。

    1. 前序遍历（递归法，迭代法）
    2. 中序遍历（递归法，迭代法）
    3. 后序遍历（递归法，迭代法）

    前中后，其实指的就是中间节点的遍历顺序，前中后序指的就是中间节点的位置：

    • 前序遍历：中左右
    • 中序遍历：左中右
    • 后序遍历：左右中

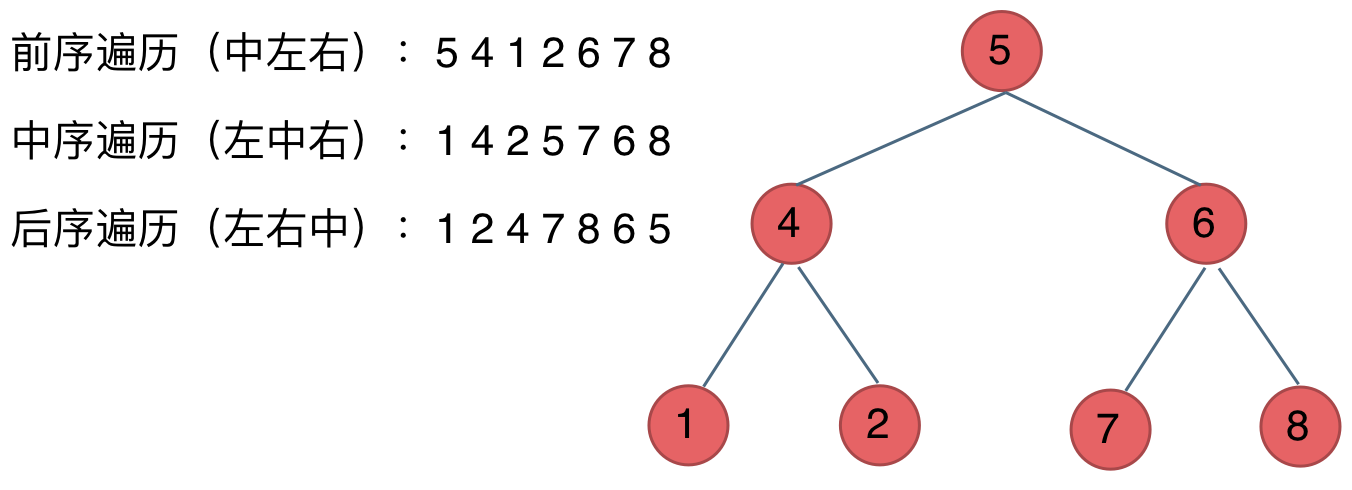
    前中后的遍历

  2. 广度优先遍历：一层一层的去遍历。

    1. 层次遍历（迭代法）

二叉树定义(链式存储)

1
2
3
4
5
6
7
8
9
10
11
12
public class TreeNode {
    int val;
  	TreeNode left;
  	TreeNode right;
  	TreeNode() {}
  	TreeNode(int val) { this.val = val; }
  	TreeNode(int val, TreeNode left, TreeNode right) {
    		this.val = val;
    		this.left = left;
    		this.right = right;
  	}
}

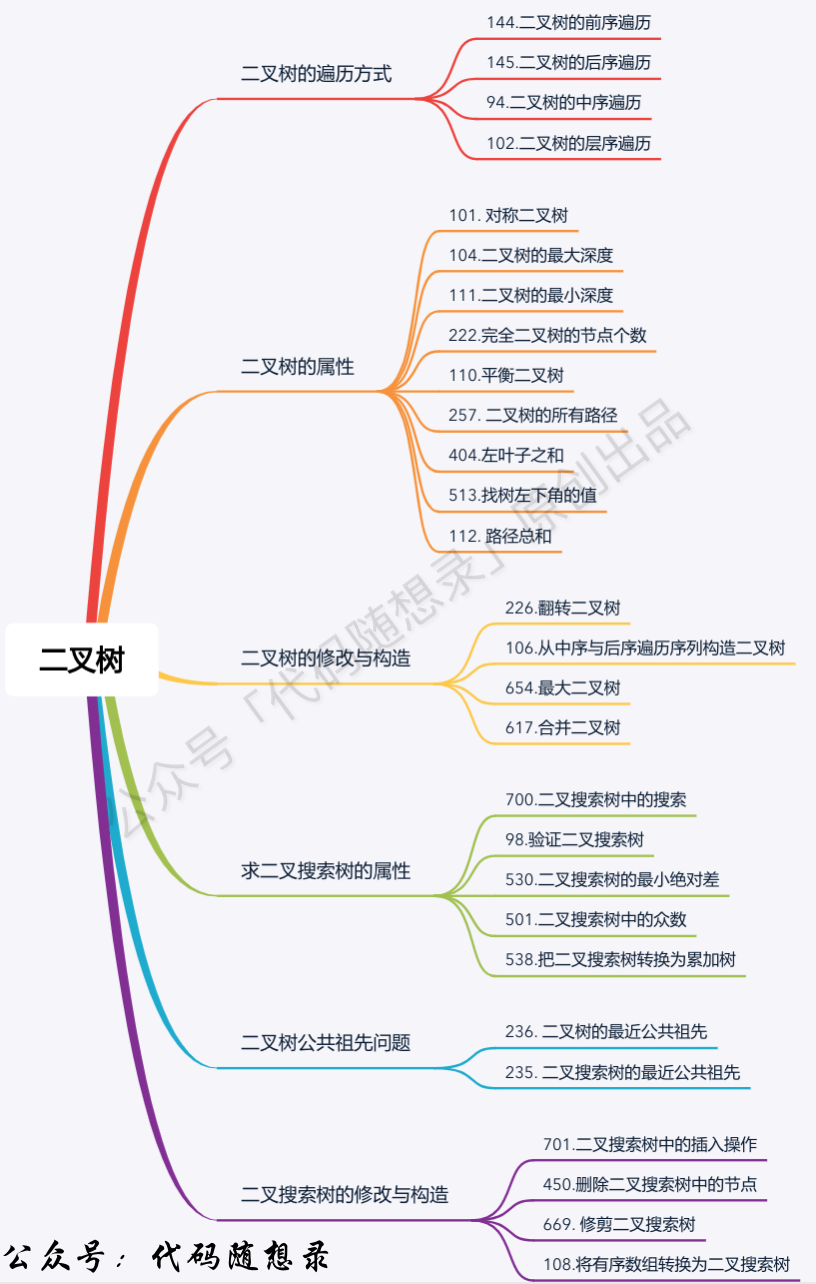
例题

例题详解见 二叉树

  • 递归遍历
    • 144.二叉树的前序遍历
    • 145.二叉树的后序遍历
    • 94.二叉树的中序遍历
  • 迭代遍历
  • 统一迭代
  • 层序遍历：
    • 102.二叉树的层序遍历
    • 107.二叉树的层次遍历II
    • 199.二叉树的右视图
    • 637.二叉树的层平均值
    • 429.N叉树的层序遍历
    • 515.在每个树行中找最大值
    • 116.填充每个节点的下一个右侧节点指针
    • 117.填充每个节点的下一个右侧节点指针II
    • 104.二叉树的最大深度
    • 111.二叉树的最小深度
  • 226.翻转二叉树
  • 101.对称二叉树 2
  • 104.二叉树的最大深度
  • 559.n叉树的最大深度
  • 111.二叉树的最小深度
  • 222.完全二叉树的节点个数
  • 110.平衡二叉树
  • 257.二叉树的所有路径
  • 404.左叶子之和