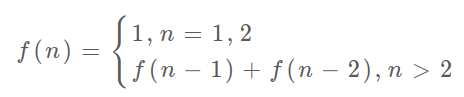一般形式 动态规划问题的一般形式就是求最值 。核心问题是 穷举 。
比如最长递增子序列,最小编辑距离这种问题
列出正确的状态转移方程,
判读是否具备最优子结构(即是否可以通过自问题的最值的道原问题的最值)
是否可以使用数据结构来优化穷举过程以避免不必要的计算。
一般包含以下三要素:
重叠子问题,最优子结构,状态转移方程
对于状态转移方程:
明确 base case -> 明确「状态」-> 明确「选择」 -> 定义 dp 数组/函数的含义 。
框架 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 def dp (状态1 , 状态2 , ... ): for 选择 in 所有可能的选择: result = 求最值(result, dp(状态1 , 状态2 , ...)) return result dp[0 ][0 ][...] = base case for 状态1 in 状态1 的所有取值: for 状态2 in 状态2 的所有取值: for ... dp[状态1 ][状态2 ][...] = 求最值(选择1 ,选择2. ..)
解题步骤
dp数组以及下标的含义
确定递推公式
dp数组初始化
确定遍历顺序
举例推导dp数组
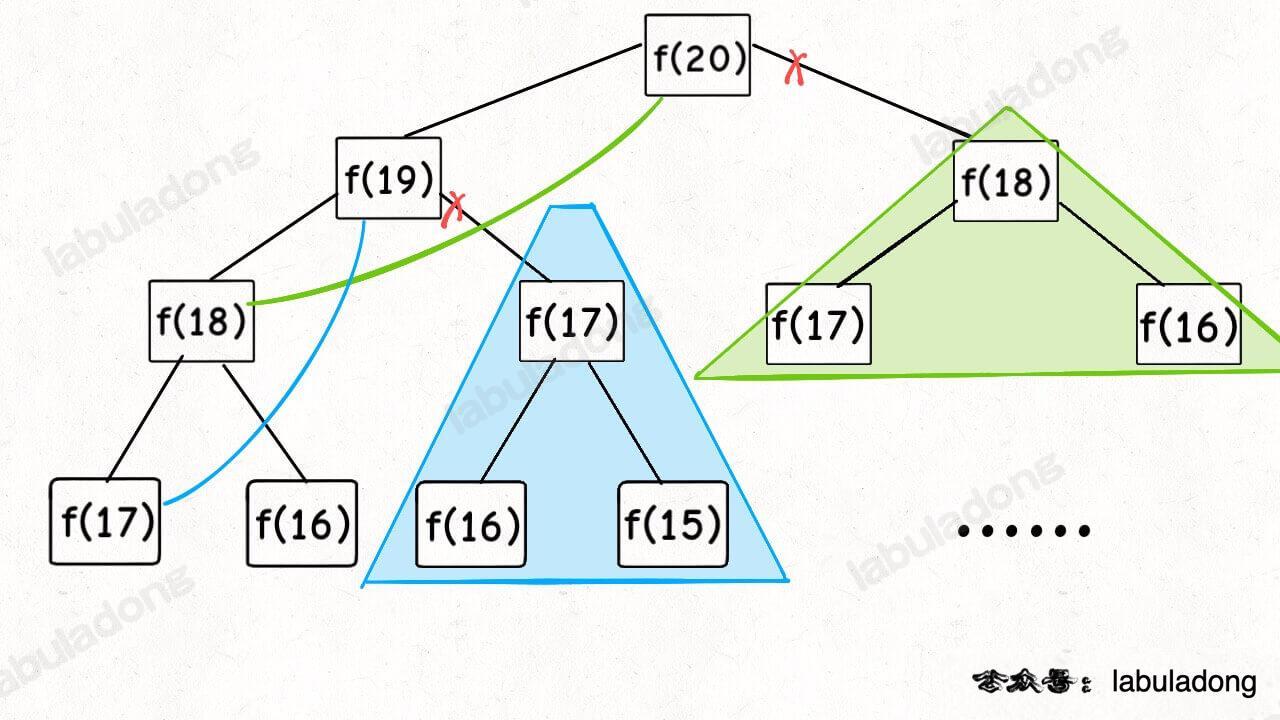
自顶向下和自底向上 以509. 斐波那契数 为例:
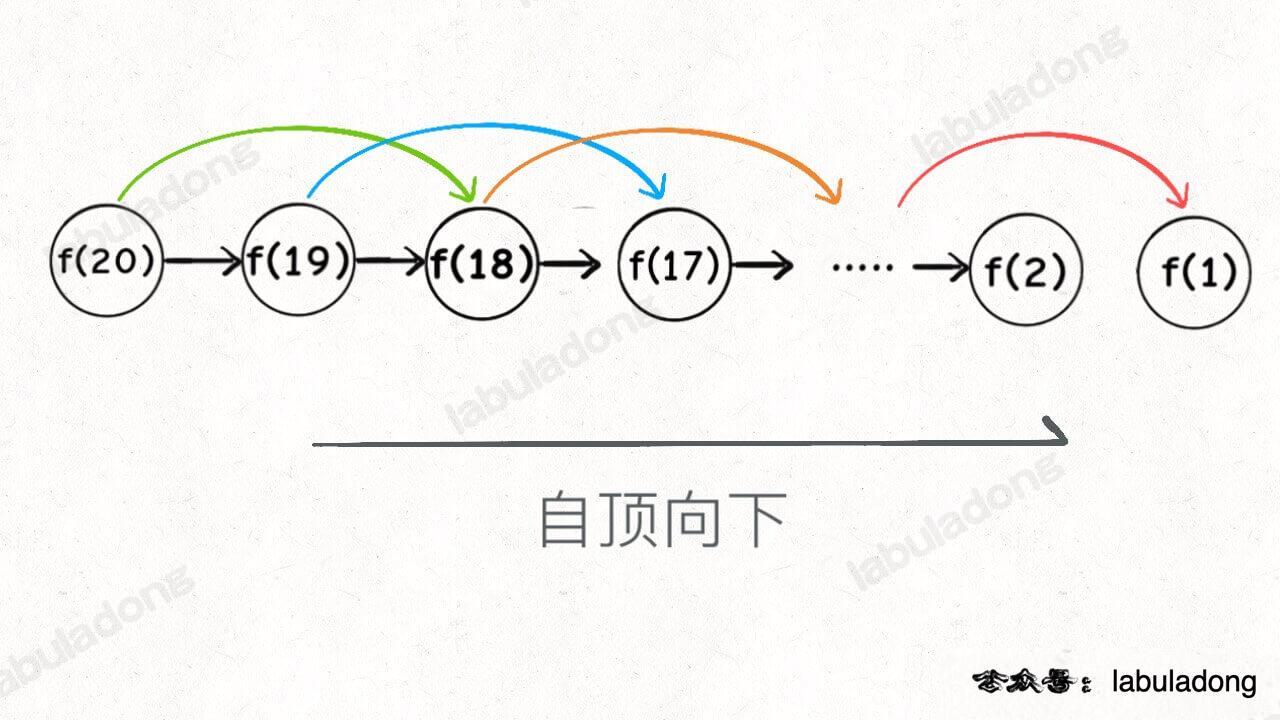
自顶向下 自顶向下就像是DFS/递归,把大问题逐渐分解规模,直到base case。从上到下,然后逐层返回答案。(注意图中含有剪枝操作,好处是可以讲原本 O(2^n)的算法简化为 O(n)
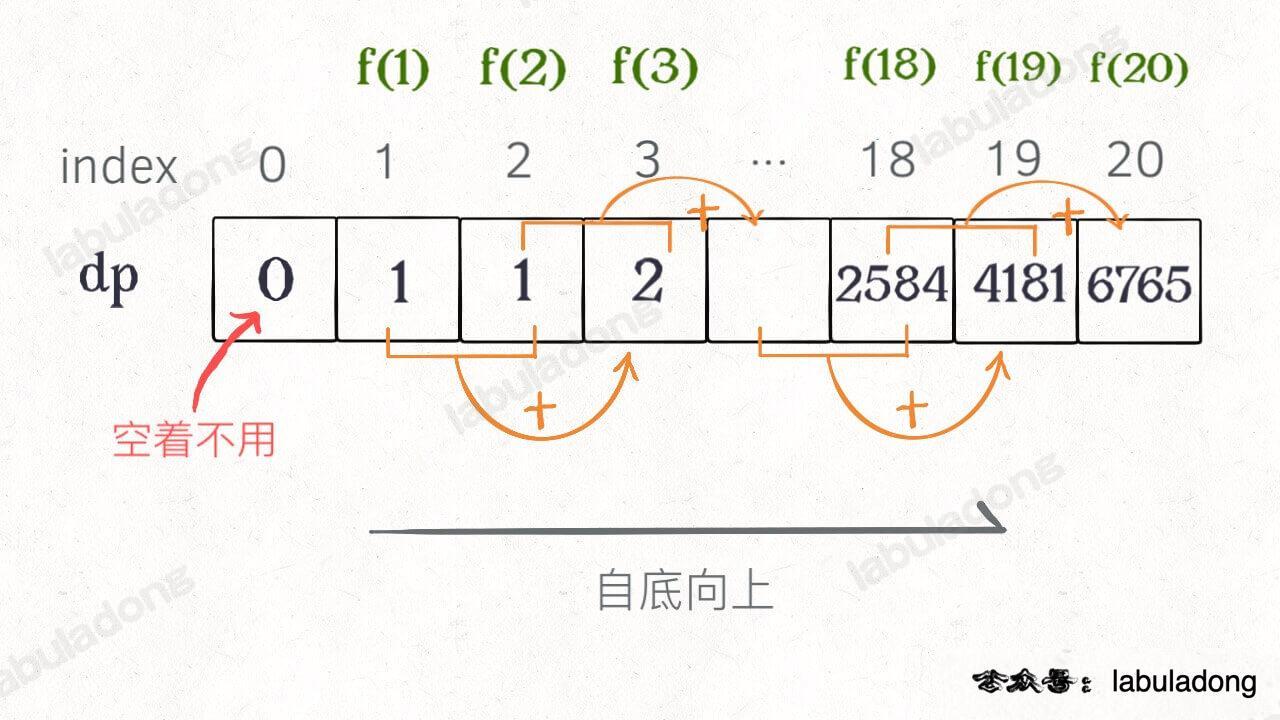
自底向上 就是从问题规模最小的问题(base case)往上推直到得到问题的答案
状态转移方程 依旧用509斐波那契数举例子:
f(n) 的函数参数会不断变化,所以你把参数 n 想做一个状态,这个状态 n 是由状态 n - 1 和状态 n - 2 转移(相加)而来,这就叫状态转移,仅此而已。
你会发现,上面的几种解法中的所有操作,例如 return f(n - 1) + f(n - 2),dp[i] = dp[i - 1] + dp[i - 2],以及对备忘录或 DP table 的初始化操作,都是围绕这个方程式的不同表现形式
最优子结构 子问题间必须相互独立 -> 最优子结构
例子:比如我想考第一名那么每一科目都考第一就能总成绩第一,但是一般数学高的话语文就会低,这就违背了子问题间相互独立
如何写状态转移方程 自己总结的:
感觉题目基本就给了dp函数的定义,可以尝试一下能否写出来base case,当前状态,以及怎么做选择
明确 状态 + 选择
状态:过程中会变化的
选择:导致状态发生改变的
明确 dp数组 定义
带入定义搞清楚 base case 以及 目标/终点 或者 查看定义是否正确 即能否转移来,子问题是什么?
如何定位重叠子问题 首先理解为什么会重叠?
这是因为在状态转移的过程中,同一个状态有多个转移过去的方式,从而导致了重复的计算。
步骤:
抽出来dp过程中递归部分中,递归出现次数多的部分 定位为了到达目标,是否有同一个状态有多种转移过去的方式
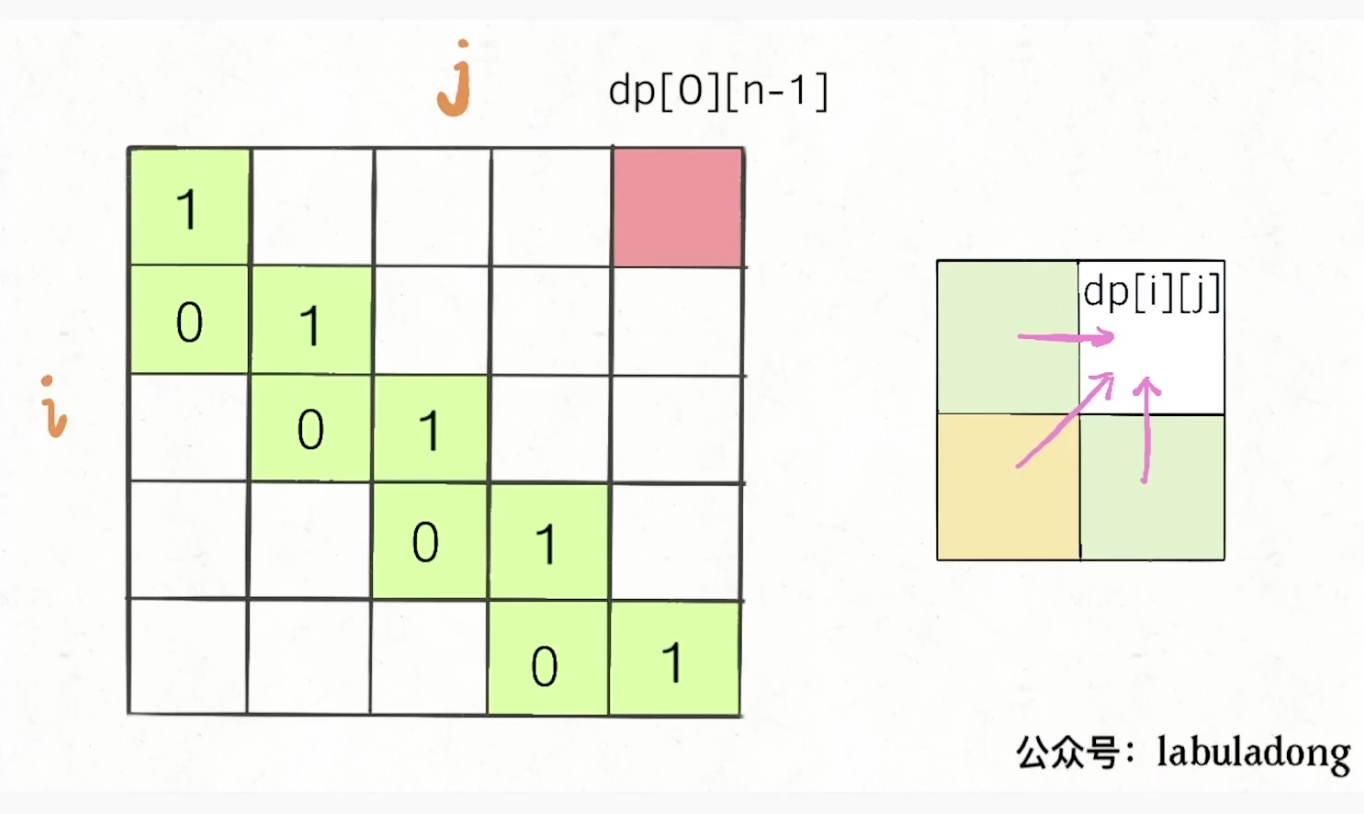
如何确定dp数组的遍历顺序 确定base case 就是起点从哪里开始,终点就是想要的结果,方向就是起点到终点
basecase 可以转移到哪里,基本就确定了转移方向
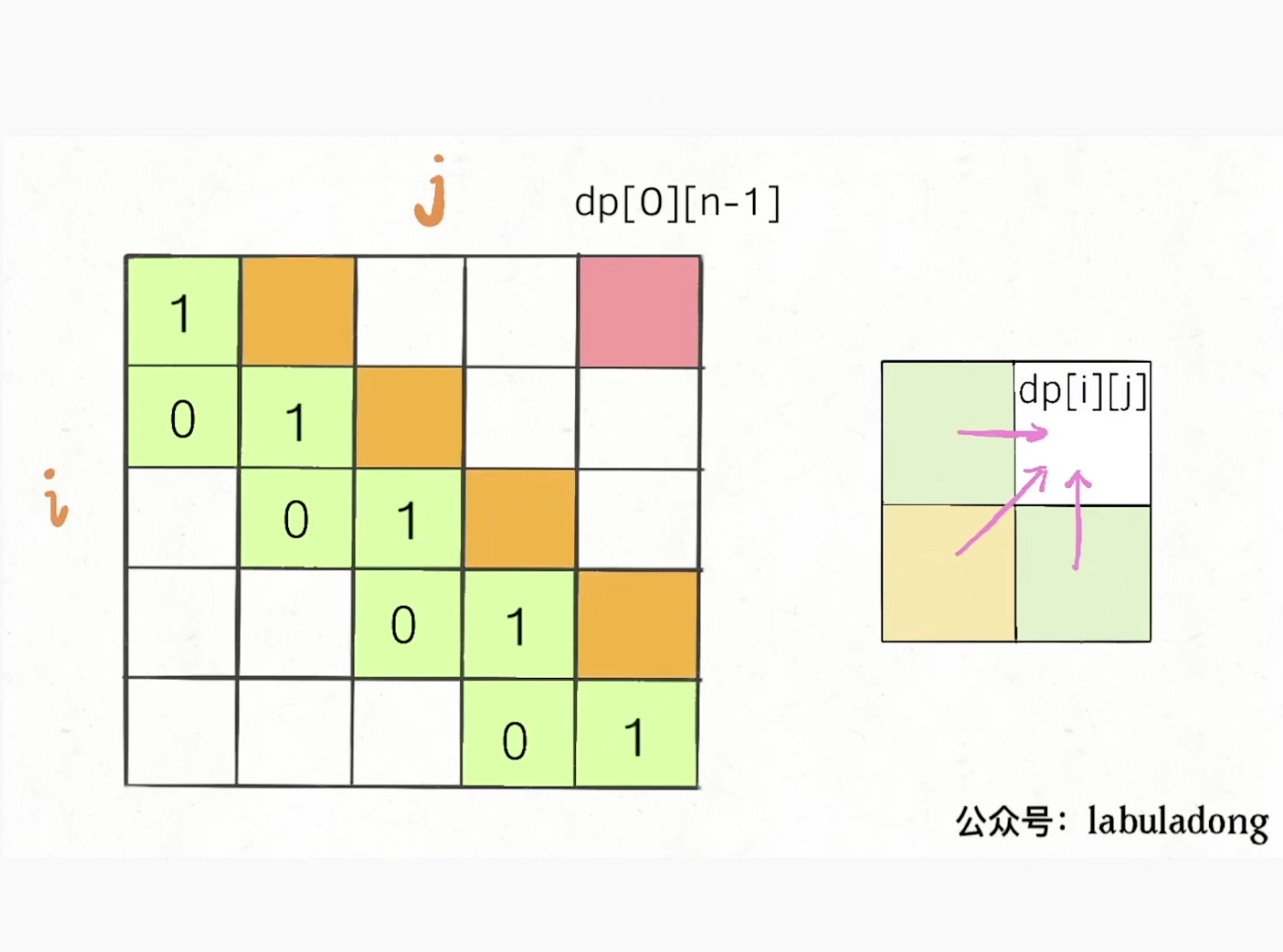
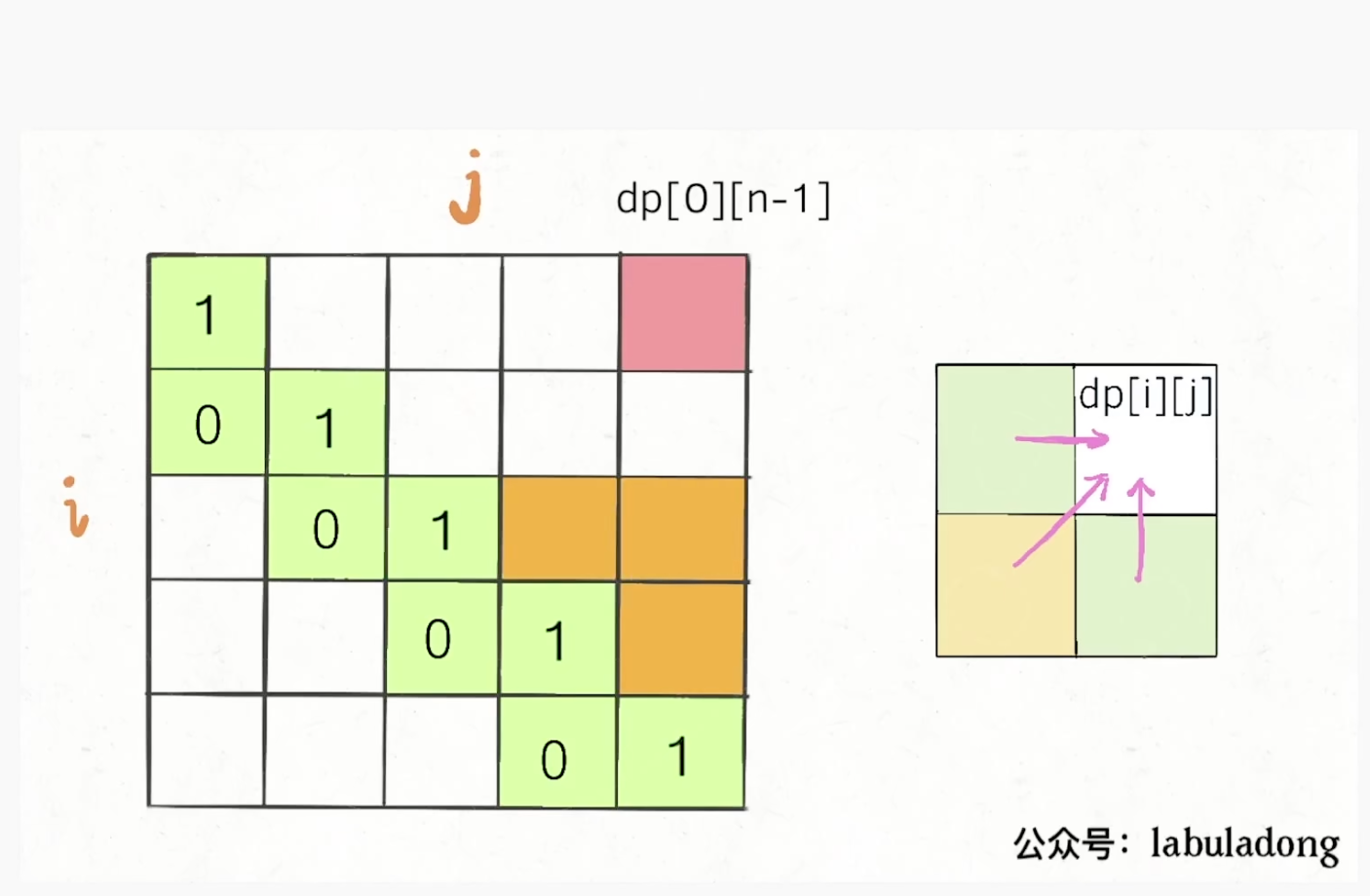
下图:我们可以从 basecase: (0, 0) (0, 1) (1, 0) 从而得到 (1, 1) 之后又可以用 (0, 1) (1, 1) (0, 2) 从而得到 (1, 2) 以此类推
再比如:
状态压缩 使用一个二进制数表示当前哪些数已被选,哪些数未被选,目的是为了可以使用位运算进行加速。
Eg: 二进制:(000… 0101) 表示1和3被visited过了
当我们需要检查值为 k 的数是否被使用时 a = (state >> k) & 1查看第k位为1(被使用)或0(未被使用)
问题分析 按照:
明确 base case -> 明确「状态」-> 明确「选择」 -> 定义 dp 数组/函数的含义 。
明确 base case:
剩余钱为0时即不需要任何其他的硬币,达到结果
明确「状态」
状态:原问题和子问题中会变化的变量:amount
由于硬币数量无限,硬币的面额也是题目给定的,只有目标金额会不断地向 base case 靠近,所以唯一的「状态」就是目标金额 amount。
明确「选择」
每选择一枚硬币,就相当于减少了目标金额。所以说所有硬币的面值,就是你的「选择」。
dp
函数:
自顶向下
函数的参数就是状态转移中会变化的量,也就是上面说到的「状态」;函数的返回值就是题目要求我们计算的量。
就本题来说,状态只有一个,即「目标金额」,题目要求我们计算凑出目标金额所需的最少硬币数量。
dp(n) 表示,输入一个目标金额 n,返回凑出目标金额 n 所需的最少硬币数量
数组:
自底向上
dp 数组的定义:当目标金额为 i 时,至少需要 dp[i] 枚硬币凑出
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 class Solution { int [] memo; public int coinChange (int [] coins, int amount) { memo = new int [amount + 1 ]; Arrays.fill(memo, -999 ); return dp(coins, amount); } private int dp (int [] coins, int amount) { if (amount == 0 ) return 0 ; if (amount < 0 ) return -1 ; if (memo[amount] != -999 ) return memo[amount]; int res = Integer.MAX_VALUE; for (int coin : coins) { int subAmount = dp(coins, amount - coin); if (subAmount < 0 ) continue ; res = Math.min(res, subAmount + 1 ); } memo[amount] = (res == Integer.MAX_VALUE) ? -1 : res; return memo[amount]; } } class Solution { public int coinChange (int [] coins, int amount) { int [] dp = new int [amount + 1 ]; Arrays.fill(dp, amount + 1 ); dp[0 ] = 0 ; for (int i = 0 ; i < dp.length; i++) { for (int coin : coins) { if (i - coin < 0 ) continue ; dp[i] = Math.min(dp[i], 1 + dp[i - coin]); } } return dp[amount] == amount + 1 ? -1 : dp[amount]; } }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 class Solution { public int minDistance (String word1, String word2) { int m = word1.length(), n = word2.length(); int [][] dp = new int [m + 1 ][n + 1 ]; for (int j = 0 ; j <= n; j++) { dp[0 ][j] = j; } for (int i = 0 ; i <= m; i++) { dp[i][0 ] = i; } dp[0 ][0 ] = 0 ; for (int i = 1 ; i <= m; i++) { for (int j = 1 ; j <= n; j++) { if (word1.charAt(i - 1 ) == word2.charAt(j - 1 )) { dp[i][j] = dp[i - 1 ][j - 1 ]; } else { dp[i][j] = Math.min( dp[i - 1 ][j] + 1 , Math.min( dp[i][j - 1 ] + 1 , dp[i - 1 ][j - 1 ] + 1 ) ); } } } return dp[m][n]; } }
如何debug 做动规的题目,写代码之前一定要把状态转移在dp数组的上具体情况模拟一遍,心中有数,确定最后推出的是想要的结果 然后再写代码,如果代码没通过就打印dp数组,看看是不是和自己预先推导的哪里不一样。如果打印出来和自己预先模拟推导是一样的,那么就是自己的递归公式、初始化或者遍历顺序有问题了。
其实就是斐波那契数
f[x] = f[x - 1] + f[x - 2]
自顶向下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 class Solution { int count = 0 ; int [] memo; public int climbStairs (int n) { memo = new int [n +1 ]; return dp(n); } private int dp (int floor) { if (floor == 0 ) { return 1 ; } if (floor < 0 ) return 0 ; if (memo[floor] != 0 ) return memo[floor]; memo[floor] = dp(floor - 2 ) + dp(floor - 1 ); return memo[floor]; } }
自底向上:
1 2 3 4 5 6 7 8 9 10 11 12 class Solution { public int climbStairs (int n) { int [] dp = new int [n + 1 ]; dp[0 ] = 1 ; dp[1 ] = 1 ; for (int i = 2 ; i < dp.length; i++) { dp[i] = dp[i - 1 ] + dp[i - 2 ]; } return dp[n]; } }
滚动优化:
1 2 3 4 5 6 7 8 9 10 11 12 13 class Solution { public int climbStairs (int n) { int a = 1 ; int b = 1 ; for (int i = 2 ; i < n + 1 ; i++) { int temp = a + b; a = b; b = temp; } return b; } }
1 2 3 4 5 6 7 8 9 10 11 12 13 class Solution { public int minCostClimbingStairs (int [] cost) { int [] dp = new int [cost.length + 1 ]; dp[0 ] = 0 ; dp[1 ] = 0 ; for (int i = 2 ; i < dp.length; i++) { dp[i] = Math.min(dp[i - 1 ] + cost[i - 1 ], dp[i - 2 ] + cost[i - 2 ]); } return dp[dp.length - 1 ]; } }
空间优化:
1 2 3 4 5 6 7 8 9 10 11 12 13 class Solution { public int minCostClimbingStairs (int [] cost) { int dpi1 = 0 , dpi2 = 0 ; int minCost = 0 ; for (int i = 2 ; i < cost.length + 1 ; i++) { minCost = Math.min(dpi1 + cost[i - 1 ], dpi2 + cost[i - 2 ]); dpi2 = dpi1; dpi1 = minCost; } return minCost; } }
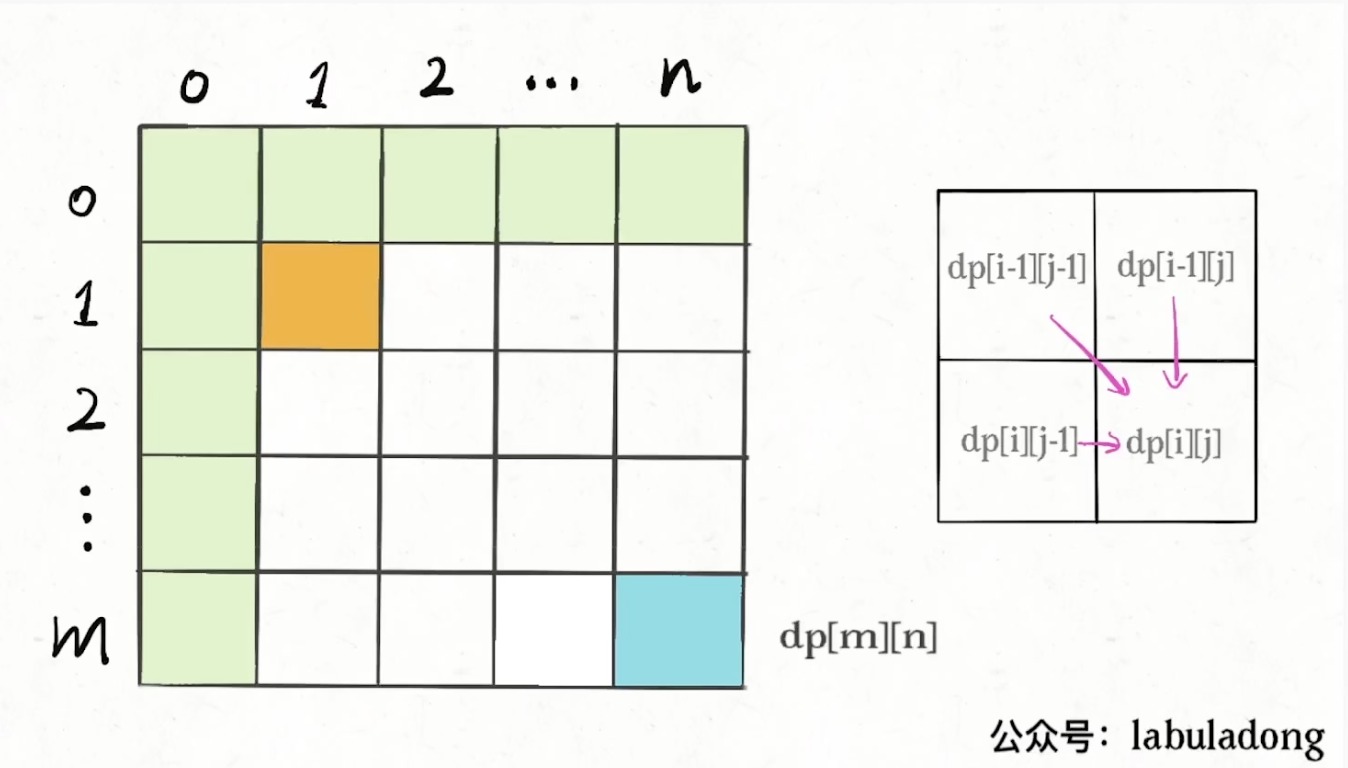
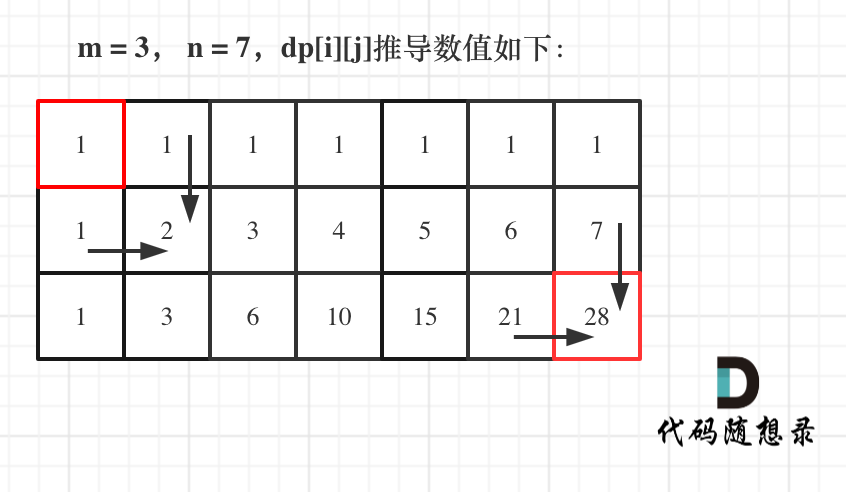
确定 dp 函数的含义:
dp[i][j] 代表 从 起点出发, 到 (i,j) 的路径方案总数
确定递推公式
由于方向只能从 上面 以及 左面 所以 dp[i][j] 会由 dp[i - 1][j] 和 dp[i][j - 1]转移而来。
dp[i - 1][j] 是从(0, 0)的位置到(i - 1, j)有几条路径,dp[i][j - 1]同理。
初始化
dp[i][0]一定都是1,因为从(0, 0)的位置到(i, 0)的路径只有一条,那么dp[0][j]也同理。
确定遍历顺序
我们要保证转移的顺序,因此 dp[i - 1][j] 和 dp[i][j - 1] 必须先由dp[i][j]计算完成
发现顺序遍历就可以达到这个效果,因此顺序遍历
举例推导dp数组
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 class Solution { public int uniquePaths (int m, int n) { int [][] dp = new int [m][n]; for (int i = 0 ; i < m; i++) dp[i][0 ] = 1 ; for (int j = 0 ; j < n; j++) dp[0 ][j] = 1 ; for (int i = 0 ; i < m; i++) { for (int j = 0 ; j < n; j++) { if (i == 0 || j == 0 ) continue ; dp[i][j] = dp[i - 1 ][j] + dp[i][j - 1 ]; } } return dp[m - 1 ][n - 1 ]; } }
自顶向下:(但是memo其实就是dp table了)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 class Solution { int [][] memo; public int uniquePaths (int m, int n) { memo = new int [m][n]; int ret = dp(m - 1 , n - 1 ); return ret; } private int dp (int i, int j) { if (i == 0 && j == 0 ) return 1 ; if (i < 0 || j < 0 ) return 0 ; if (memo[i][j] != 0 ) return memo[i][j]; memo[i][j] = dp(i - 1 , j) + dp(i, j - 1 ); return memo[i][j]; } }
总体和 62 差别不大,但是在初始化时以及转移方程需要特别处理一下:
确定dp数组(dp table)以及下标的含义
dp[i][j] :表示从(0 ,0)出发,到(i, j) 有dp[i][j]条不同的路径。
确定递推公式
递推公式和62.不同路径一样,dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
但这里需要注意一点,因为有了障碍,(i, j)如果就是障碍的话应该就保持初始状态(初始状态为0)
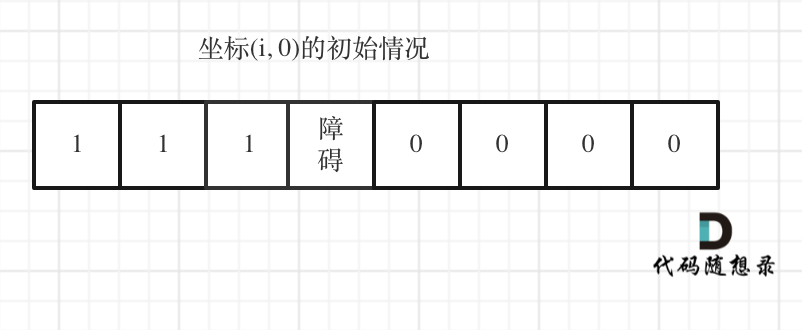
初始化
这里的区分比较大,主要是由于在第一行和第一列如果有了障碍,那么这个障碍之后的全部都应为0
确定遍历顺序
一定是从左到右一层一层遍历,这样保证推导dp[i][j]的时候,dp[i - 1][j] 和 dp[i][j - 1]一定是有数值。
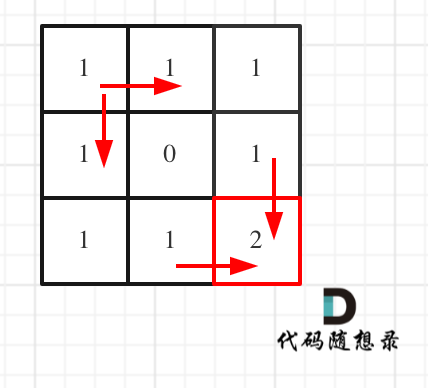
举例推导dp数组
自底向上:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 class Solution { public int uniquePathsWithObstacles (int [][] obstacleGrid) { int m = obstacleGrid.length, n = obstacleGrid[0 ].length; int [][] dp = new int [m][n]; for (int i = 0 ; i < m; i++) { if (obstacleGrid[i][0 ] == 1 ) break ; dp[i][0 ] = 1 ; } for (int j = 0 ; j < n; j++) { if (obstacleGrid[0 ][j] == 1 ) break ; dp[0 ][j] = 1 ; } for (int i = 0 ; i < m; i++) { for (int j = 0 ; j < n; j++) { if (i == 0 || j == 0 ) continue ; if (obstacleGrid[i][j] == 1 ) continue ; dp[i][j] = dp[i - 1 ][j] + dp[i][j - 1 ]; } } return dp[m - 1 ][n - 1 ]; } }
自顶向下 (记忆化搜索)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 class Solution { int [][] memo; int [][] grid; public int uniquePathsWithObstacles (int [][] obstacleGrid) { int m = obstacleGrid.length, n = obstacleGrid[0 ].length; memo = new int [m][n]; grid = obstacleGrid; return dp(m - 1 , n - 1 ); } private int dp (int i, int j) { if (i == 0 && j == 0 && grid[i][j] != 1 ) return 1 ; if (i < 0 || j < 0 ) return 0 ; if (grid[i][j] == 1 ) return 0 ; if (memo[i][j] != 0 ) return memo[i][j]; memo[i][j] = dp(i - 1 , j) + dp(i, j - 1 ); return memo[i][j]; } }
这道题主要难在怎么分:
一开始思维方式是dfs,求出来所有组合,然后每一个组合都要相乘,比较最大值,但是显然这样我们需要非常大的空间来存储。
用dp[n]来表示整数为n时,我们能够得到的最大乘积。
转移方程比较难想:
比方说 n = 4,我们可以把 4 拆分成 1 + 3, 2 + 2,对应的乘积就是 1 * 3, 2 * 2。但此时我们直接比较 1 * 3, 2 * 2 的大小还不够,因为 3, 2 它们可能还会被分解成 1 * 2, 1 * 1,也就是说把 n = 4 进一步分解成 1 * (1 * 2), 2 * (1 * 1),这两种可能也要纳入考虑。
到底需不需要进一步分解呢?不知道,所以我们都穷举一遍取最大值就可以了。
1 2 3 4 5 6 integerBreak(4 ) = max(1 * 3 , 1 * integerBreak(3 ), 2 * 2 , 2 * integerBreak(2 )) = max( 1 * max(3 , integerBreak(3 )), 2 * max(2 , integerBreak(2 )) )
其实就是拿着刚分解完的结果以及未来要分解的结果求最大值。
再加上 memo 来消除重叠子问题:
自顶向下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 class Solution { int [] memo; public int integerBreak (int n) { memo = new int [n + 1 ]; return dp(n); } private int dp (int n) { if (n == 0 ) return 0 ; if (n == 1 ) return 1 ; if (memo[n] != 0 ) return memo[n]; int result = Integer.MIN_VALUE; for (int i = 1 ; i < n; i++) { result = Math.max( result, i * Math.max(dp(n - i), n - i) ); } memo[n] = result; return memo[n]; } }
自底向上:
整体思路是差不多的,都是考虑了两种情况:
dp[i]要么从 dp[i - j] * j 转移而来 要么从 (i - j) * j 转移而来,
由于dp[i]之前已经被赋值,因此我们仍需要加入最大值判断
比较特殊的点在于初始化:
严格从dp[i]的定义来说,dp[0] dp[1] 就不应该初始化,也就是没有意义的数值。这里我只初始化dp[2] = 1,从dp[i]的定义来说,拆分数字2,得到的最大乘积是1。
以及遍历顺序:
dp[i] 是依靠 dp[i - j]的状态,所以遍历i一定是从前向后遍历,先有dp[i - j]再有dp[i]。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 class Solution { public int integerBreak (int n) { int [] dp = new int [n + 1 ]; dp[2 ] = 1 ; for (int i = 3 ; i <= n; i++) { for (int j = 1 ; j < i; j++) { dp[i] = Math.max( dp[i], Math.max( dp[i - j] * j, (i - j) * j ) ); } } return dp[n]; } }
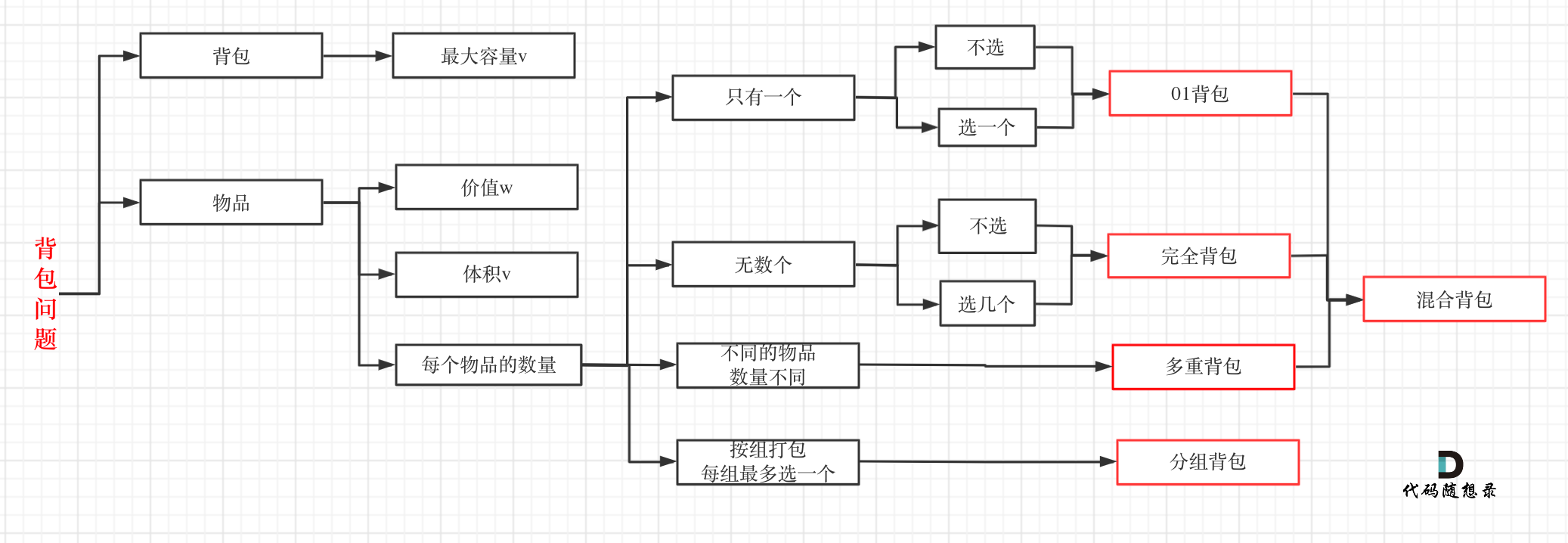
背包问题 见 背包问题 中包含背包问题的思路