单调队列和单调栈

单调(Monotonic)队列和单调栈

灵茶山艾府 - 单调栈

灵茶山艾府 - 单调队列

概念：DIY的一个队列，队列中的元素是单调递增或者单调递减

目的是为了找到 下一个更大或更小元素

比如：一个递减栈，从栈底到栈顶递减，用来找出从左往右遍历第一个比它大的位置。

单调栈

739. 每日温度

通过这个题搞清楚从右向左以及从左向右的单调栈的区别。

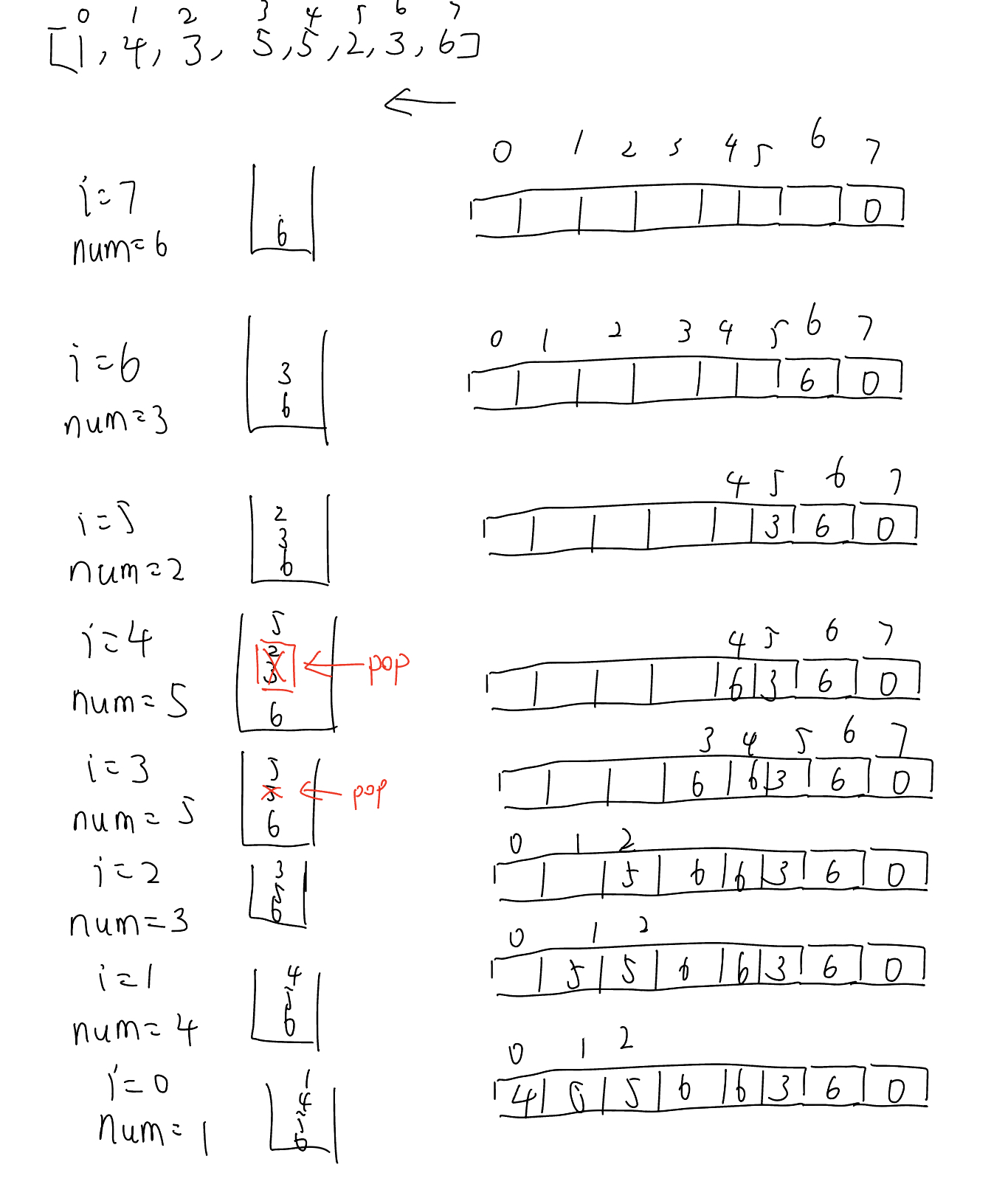
假设数组[1, 4, 3, 5, 5, 2, 3, 6]

从右向左遍历：本质上是把下一个更大的数存到了栈里

检查栈顶以及当前元素num

1. 若 num >= 栈顶 pop 掉栈中元素，从而保证栈底到栈顶是单调递减的

2. 更新answer[i]为栈顶元素

3. 将num加入栈顶

class Solution {
    public int[] dailyTemperatures(int[] temperatures) {
        Stack<Integer> stack = new Stack<>();
        int n = temperatures.length;
        int[] answer = new int[n];
        for (int i = n - 1; i >= 0; i--) {
            while (!stack.isEmpty() && temperatures[stack.peek()] <= temperatures[i]) {
                stack.pop();
            }
            if (!stack.isEmpty()) {
                answer[i] = stack.peek() - i;
            }            
            stack.push(i);
        }
        return answer;
    }
}

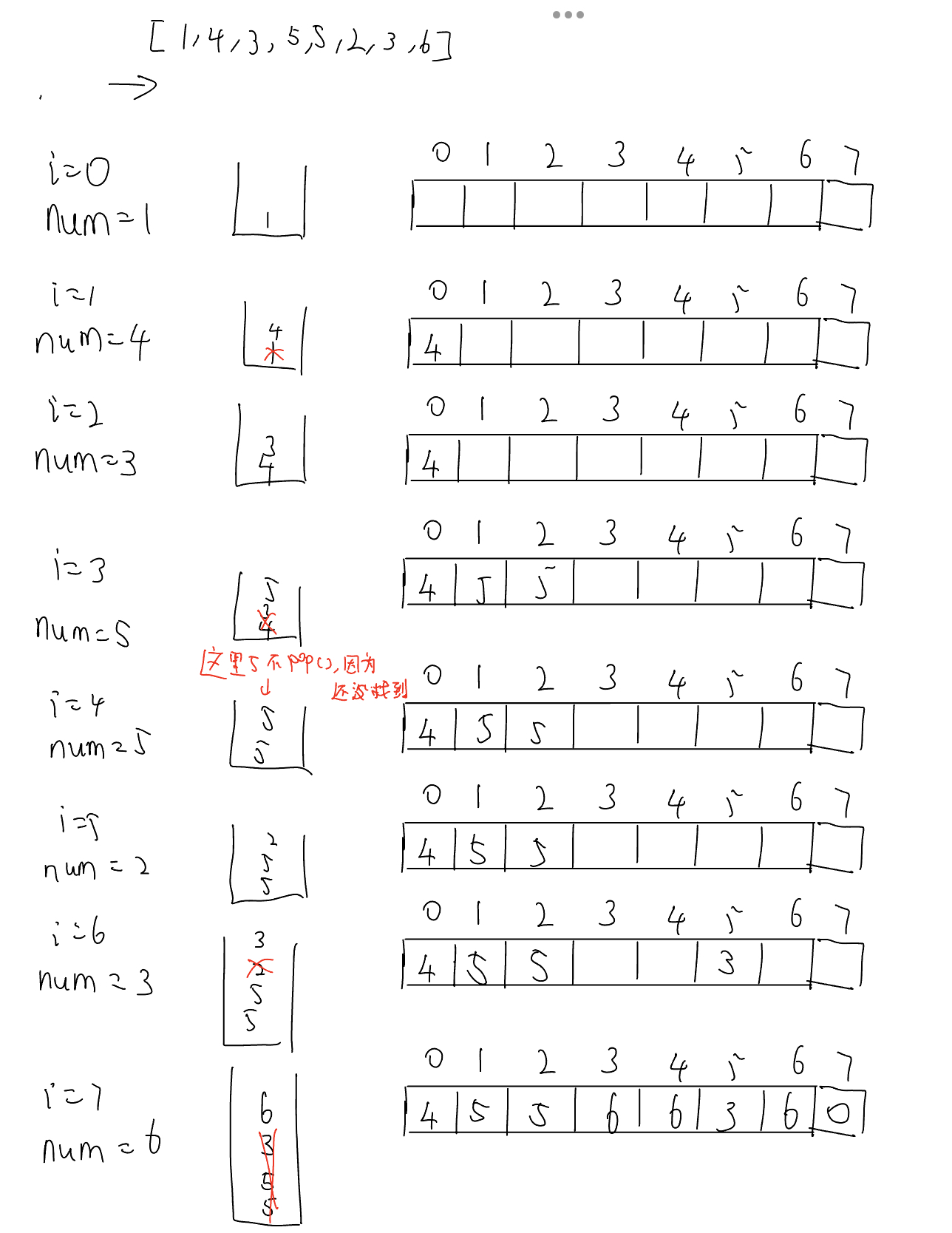
从左向右：本质上是把还没来得及找到下一个更大元素的当前元素放在栈里

一旦发现元素 > 栈顶元素，去掉老的，更新答案

class Solution {
    public int[] dailyTemperatures(int[] temperatures) {
        Stack<Integer> stack = new Stack<>();
        int n = temperatures.length;
        int[] answer = new int[n];
        for (int i = 0; i < n; i++) {
            while (!stack.isEmpty() && temperatures[stack.peek()] < temperatures[i]) {
                int idx = stack.pop();
                answer[idx] = i - idx;
            }
            if (stack.isEmpty()) answer[i] = 0;
            stack.push(i);
        }
        return answer;
    }
}

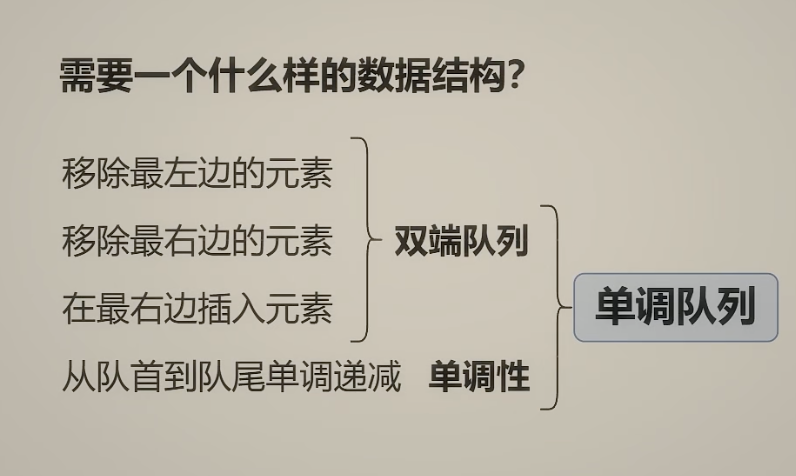
单调队列

239. 滑动窗口最大值

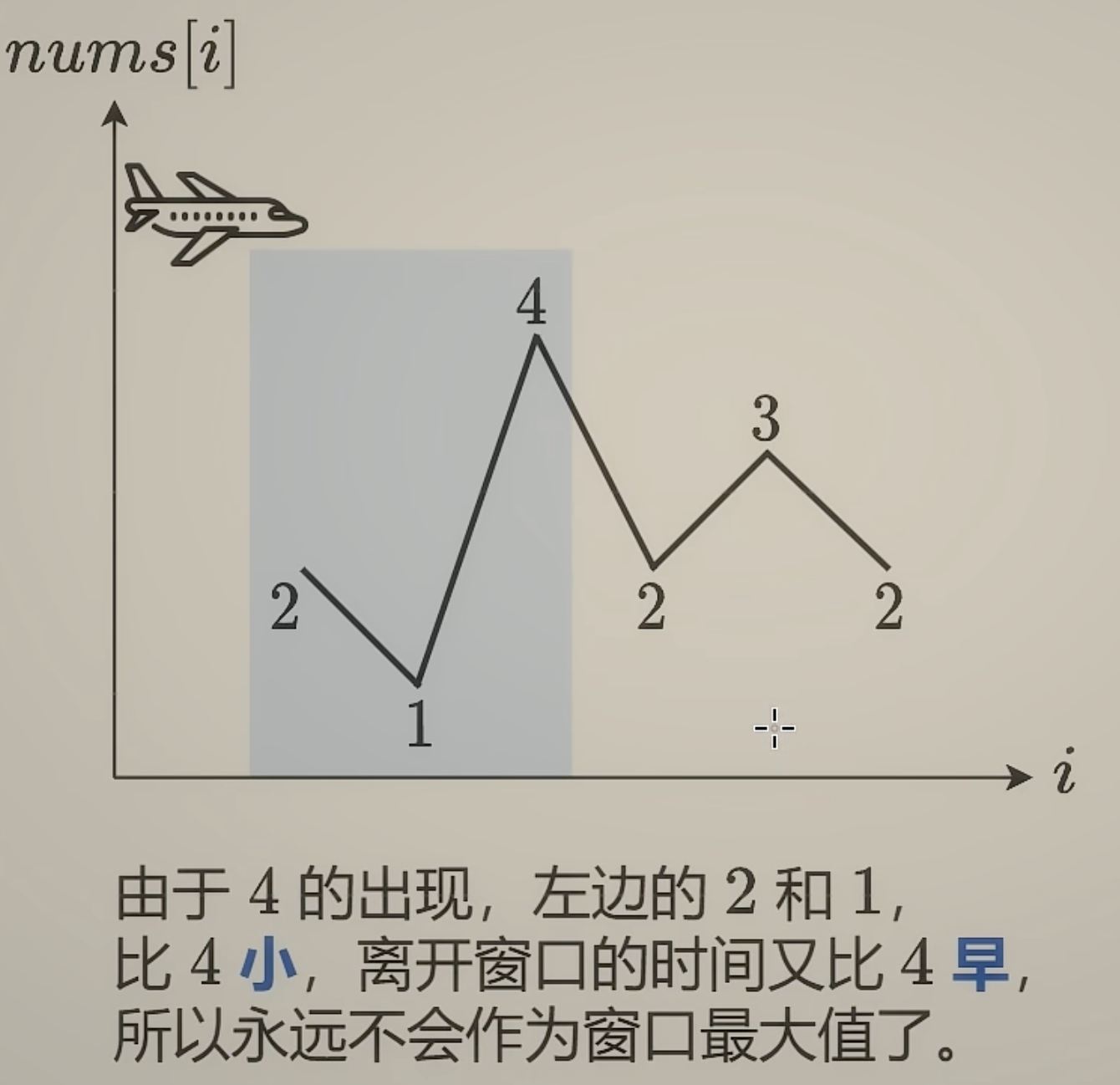
这道题还涵盖了一个滑动窗口的框架

双指针 滑动窗口 section

class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        List<Integer> res = new ArrayList<>();
        Deque<Integer> dq = new LinkedList<>();
        int n = nums.length;
        for (int i = 0; i < n; i++) {
            // 滑动窗口框架：
            // 1. 入
            int num = nums[i];
            while (!dq.isEmpty() && nums[dq.peekLast()] <= num) {
                dq.pollLast();
            }
            dq.addLast(i);
            // 2. 出
            if (i - dq.peekFirst() >= k) {
                dq.pollFirst();
            }
            // 3. 记录答案
            if (i >= k - 1) {
                res.add(nums[dq.peekFirst()]);
            }
        }

        int[] resultArray = new int[res.size()];
        for (int i = 0; i < res.size(); i++) {
            resultArray[i] = res.get(i);
        }
        return resultArray;
    }
}

题目

239. 滑动窗口最大值

需要自己设计一个数据结构支持：

1. Pop()
2. Push()
3. getMaxValue()

数据结构内部单调递减，也就是单调队列

class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        MonolithicDownQueue monolithicDownQueue = new MonolithicDownQueue();
        int left = 0, right = 0;
        List<Integer> res = new ArrayList<>();
        while (right < k) {
            monolithicDownQueue.push(nums[right]);
            right++;
        }
        res.add(monolithicDownQueue.getMaxValue());
        while (right < nums.length) {
            monolithicDownQueue.pop(nums[left]);
            monolithicDownQueue.push(nums[right]);
            res.add(monolithicDownQueue.getMaxValue());
            left++;
            right++;
        }
        return res.stream().mapToInt(i -> i).toArray();
    }

    class MonolithicDownQueue {
        Deque<Integer> dq = new ArrayDeque<>();
        void pop(int value) {
            if (!dq.isEmpty() && dq.peekFirst() == value) {
                dq.removeFirst();
            }
        }

        void push(int value) {
            // 保证数据结构内部单调递减即碰见新元素时，如果新元素大于队尾元素，移除队尾的元素
            while (!dq.isEmpty() && value > dq.peekLast()) {
                dq.removeLast();
            }
            dq.addLast(value);
        }

        int getMaxValue() {
            return dq.isEmpty() ? 0 : dq.peekFirst();
        }
    }

}

1944. 队列中可以看到的人数

class Solution {
    public int[] canSeePersonsCount(int[] heights) {
        Deque<Integer> dq = new ArrayDeque<>();
        int n = heights.length;
        int[] res = new int[n];
        if (n == 0) return new int[0];
        for (int i = n - 1; i >= 0; i--) {
            while (!dq.isEmpty() && dq.peekLast() < heights[i]) {
                res[i]++;
                dq.pollLast();
            }
            if (!dq.isEmpty()) res[i] += 1;
            dq.addLast(heights[i]);
        }
        return res;
    }
}