回溯
此教程参考 labuladong - 回溯算法框架 以及 代码随想录 - 回溯篇
感谢支持!
回溯算法框架
回溯算法和我们常说的 DFS 算法非常类似,本质上就是一种暴力穷举算法。
回溯算法和 DFS 算法的细微差别是:回溯算法是在遍历「树枝」,DFS 算法是在遍历「节点」
关于回溯的撤销
回溯撤销操作通常在以下情况下执行:
- 当你已经完成了当前层级的所有操作,并且需要返回到上一层级以尝试其他可能性时。在这种情况下,撤销操作可以帮助你恢复到之前的状态,从而允许你继续探索其他可能的解决方案。
- 当你在当前层级上遇到了一个不满足约束条件的解时。在这种情况下,你需要撤销在这个解上所做的操作,以便回到之前的状态并尝试其他选择。
在递归算法中,回溯撤销操作通常在递归调用之后执行。这是因为,在递归调用返回时,你已经完成了该层级的所有操作,现在需要恢复到之前的状态以便探索其他可能性。
回溯撤销操作应在完成当前层级的所有操作后执行,以便在回溯过程中恢复到之前的状态并尝试其他可能性。
步骤
为了解决回溯的相关问题,就是解决一个决策树的遍历
站在回溯树的一个节点上,需要思考 3 个问题:
1、路径:也就是已经做出的选择。
2、选择列表:也就是你当前可以做的选择。
3、结束条件:也就是到达决策树底层,无法再做选择的条件。
1 | result = [] |
核心就是 for 循环里面的递归,在递归调用之前「做选择」,在递归调用之后「撤销选择」
应用场景
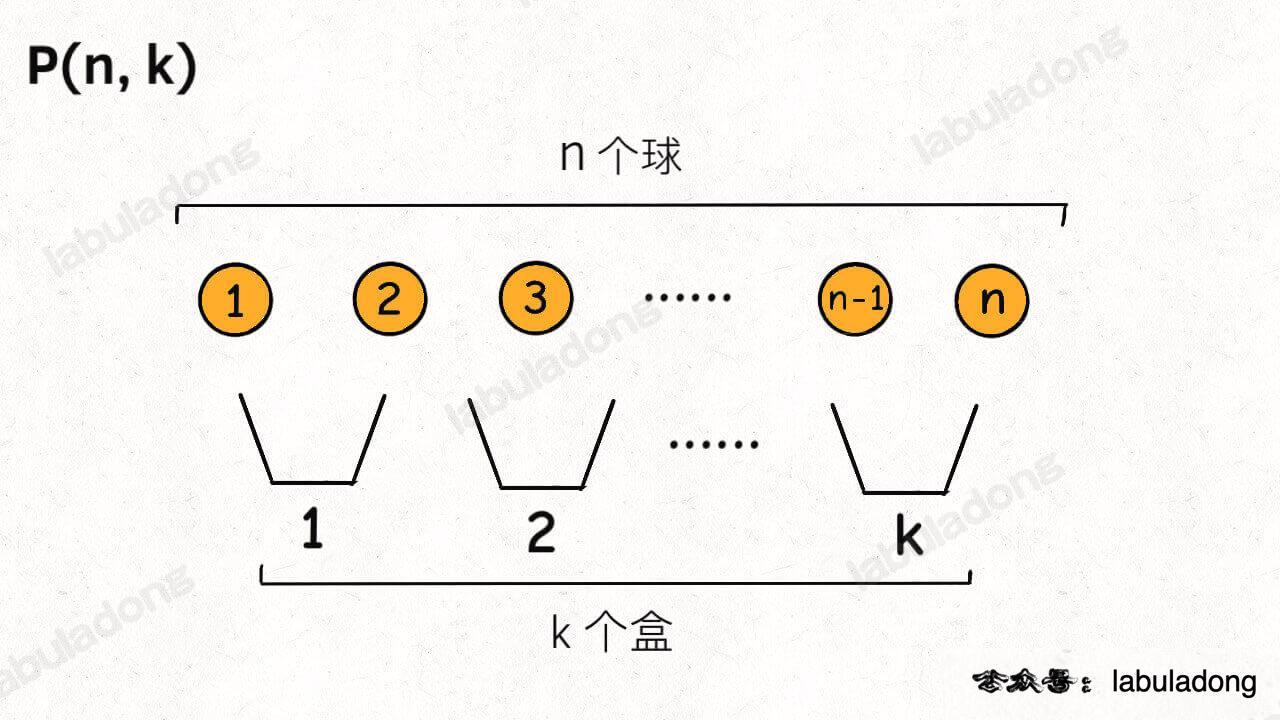
排列:N个数按一定规则全排列,有几种排列方式
组合:N个数里面按一定规则找出k个数的集合
子集:一个N个数的集合里有多少符合条件的子集
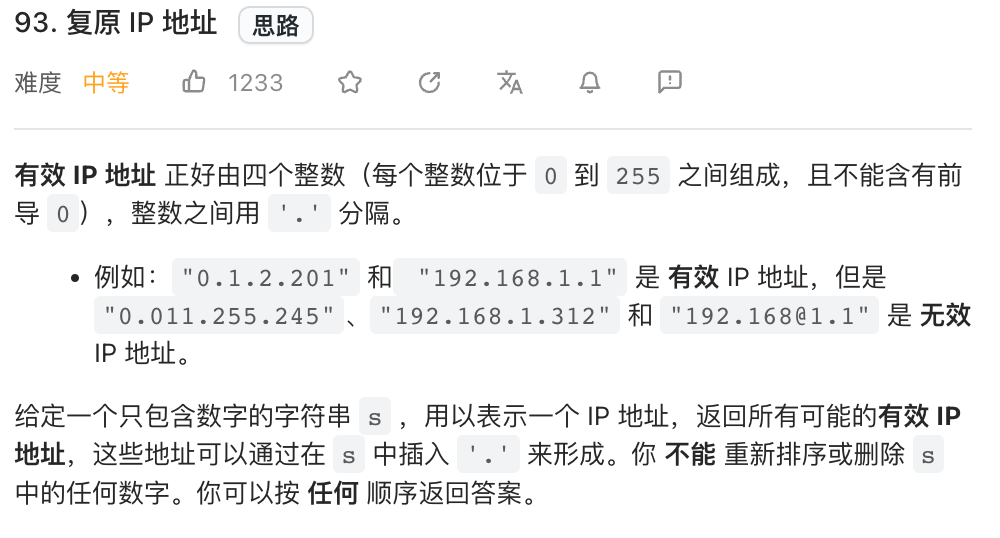
切割:一个字符串按一定规则有几种切割方式
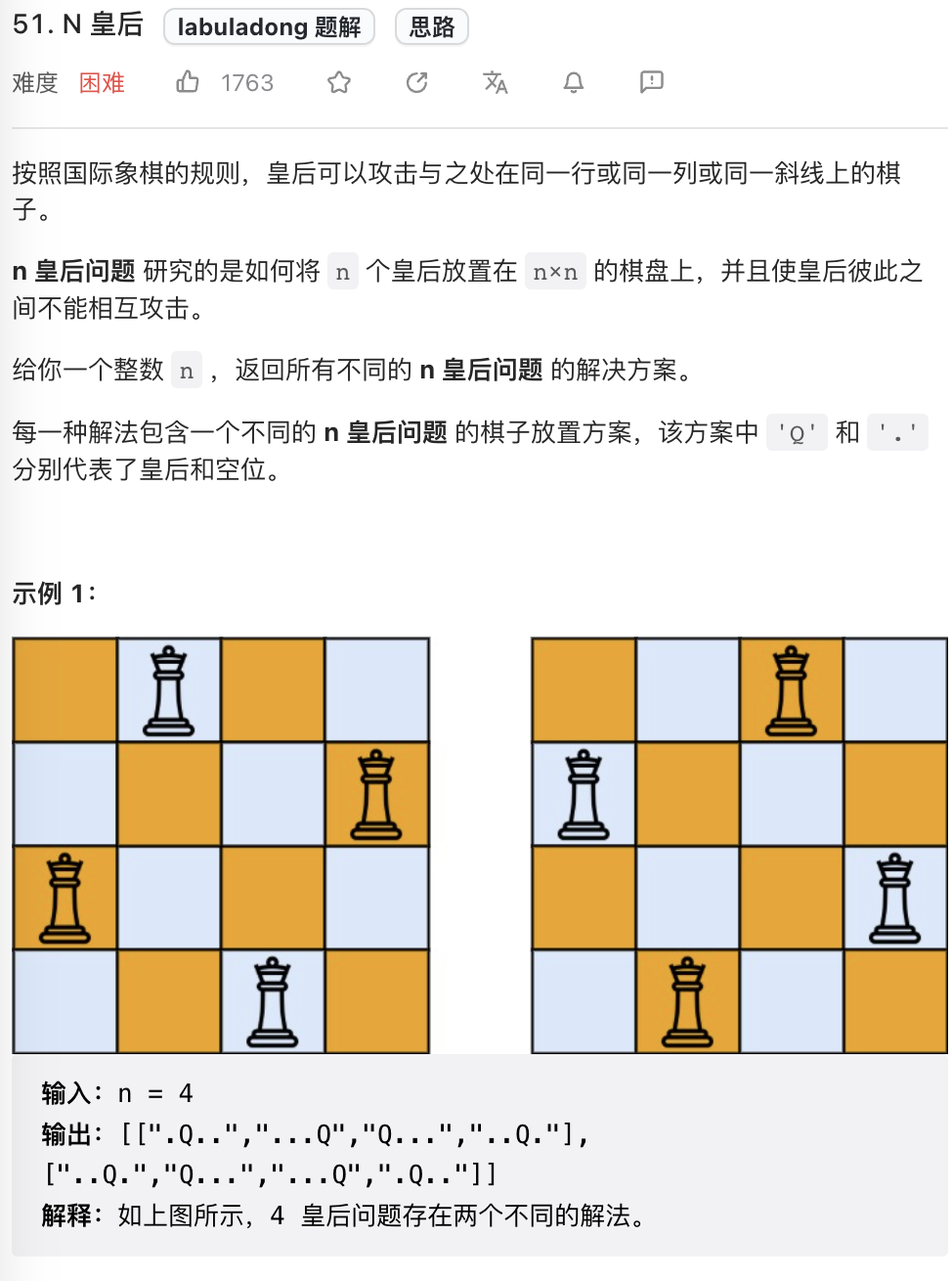
棋盘:N皇后,解数独等等
关键在于需要暴力去搜索的算法
总结
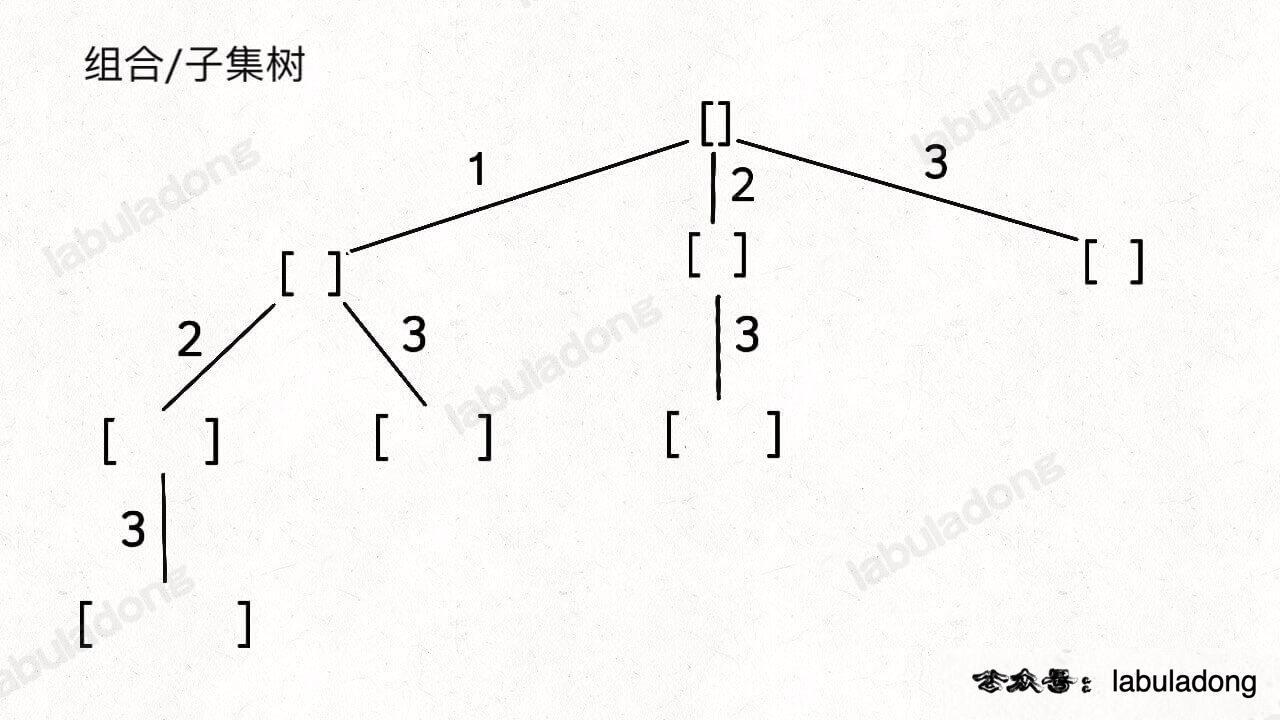
组合 and 子集
组合
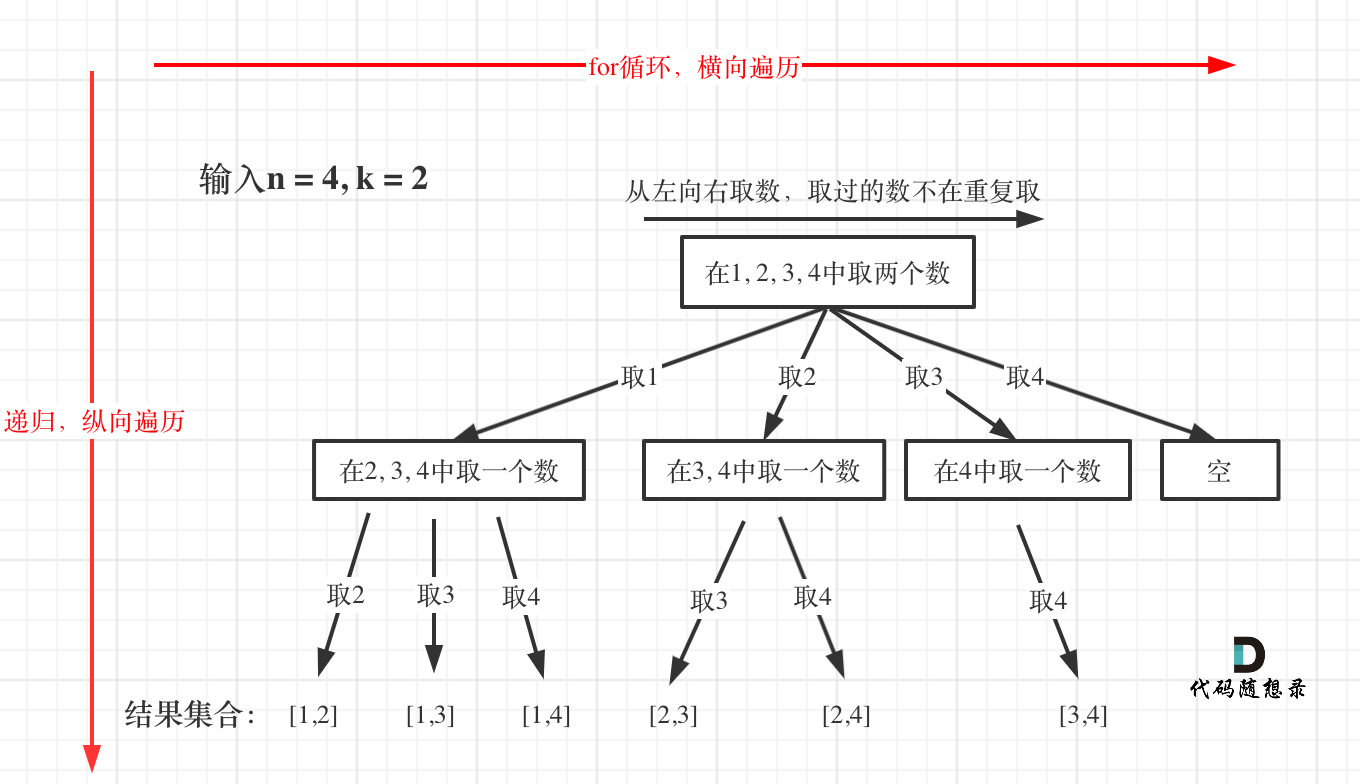
for循环横向遍历,递归纵向遍历,回溯不断调整结果集