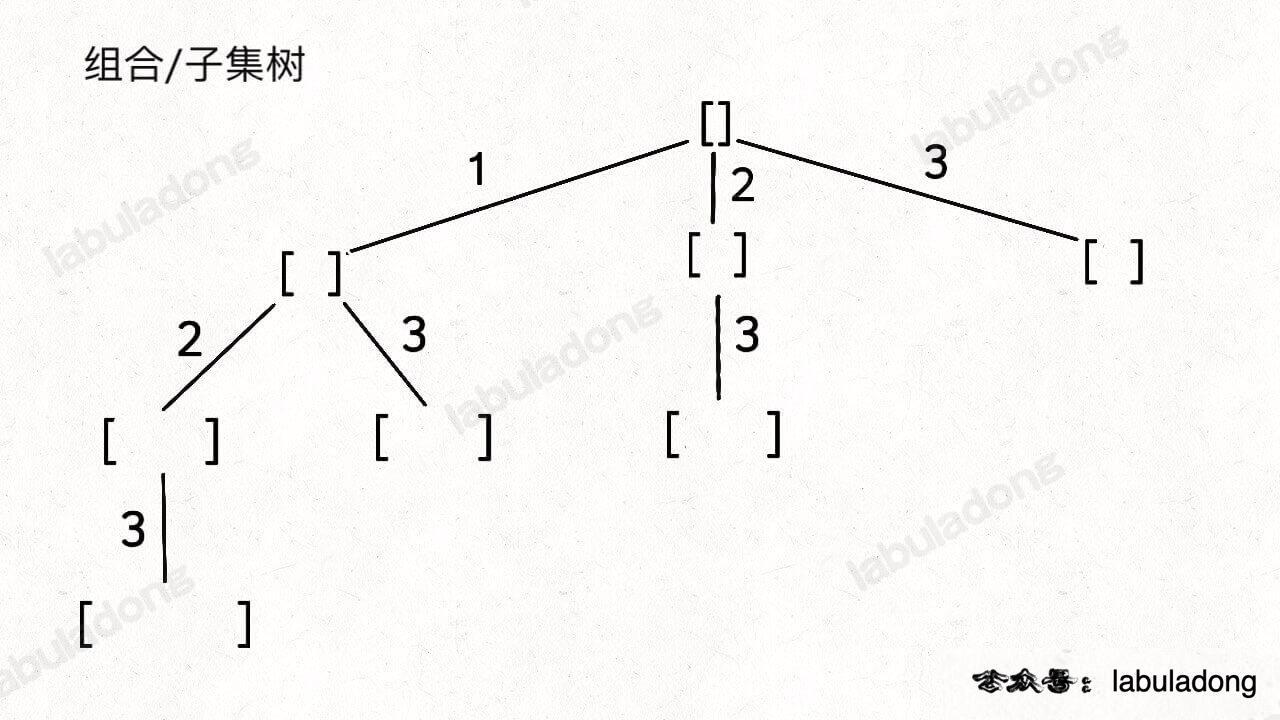
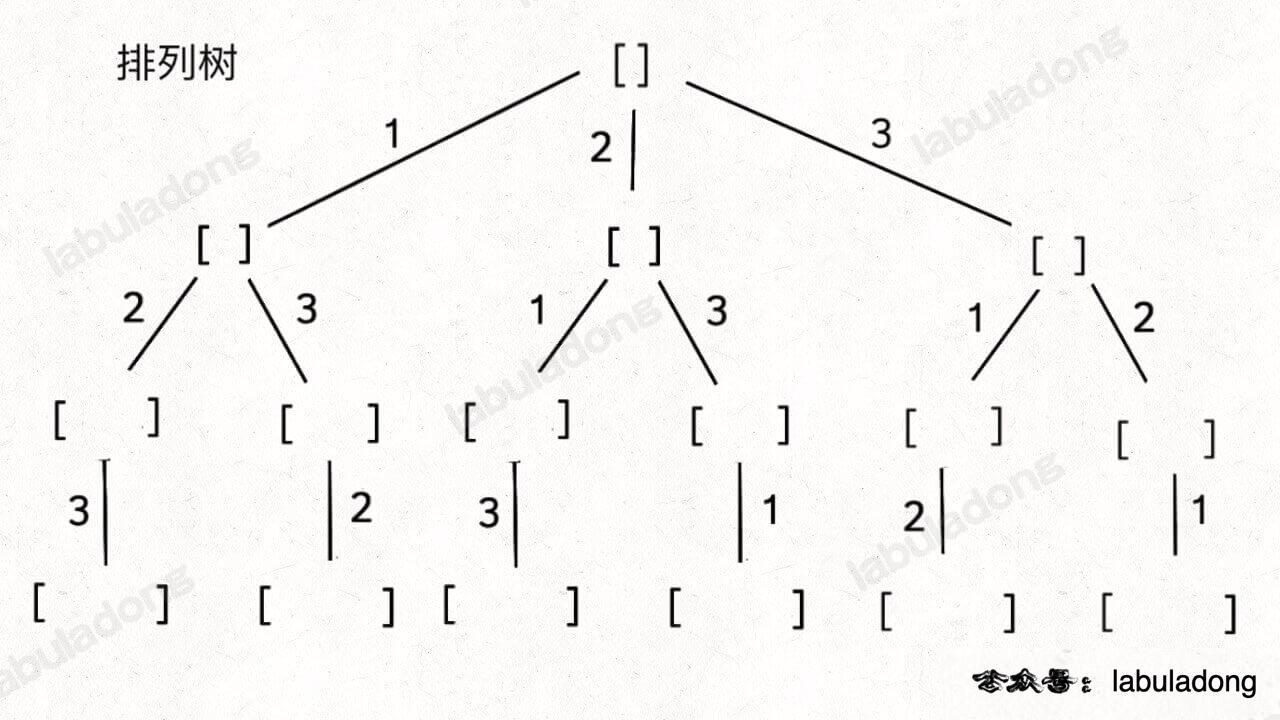
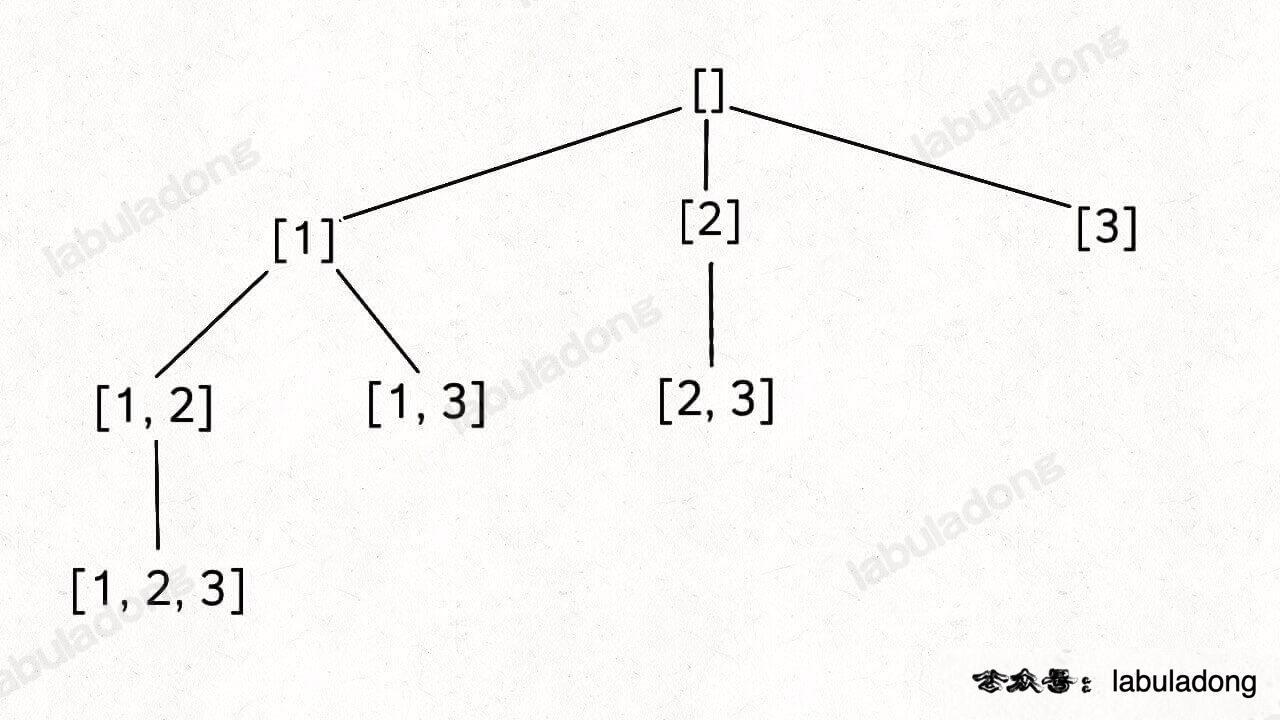
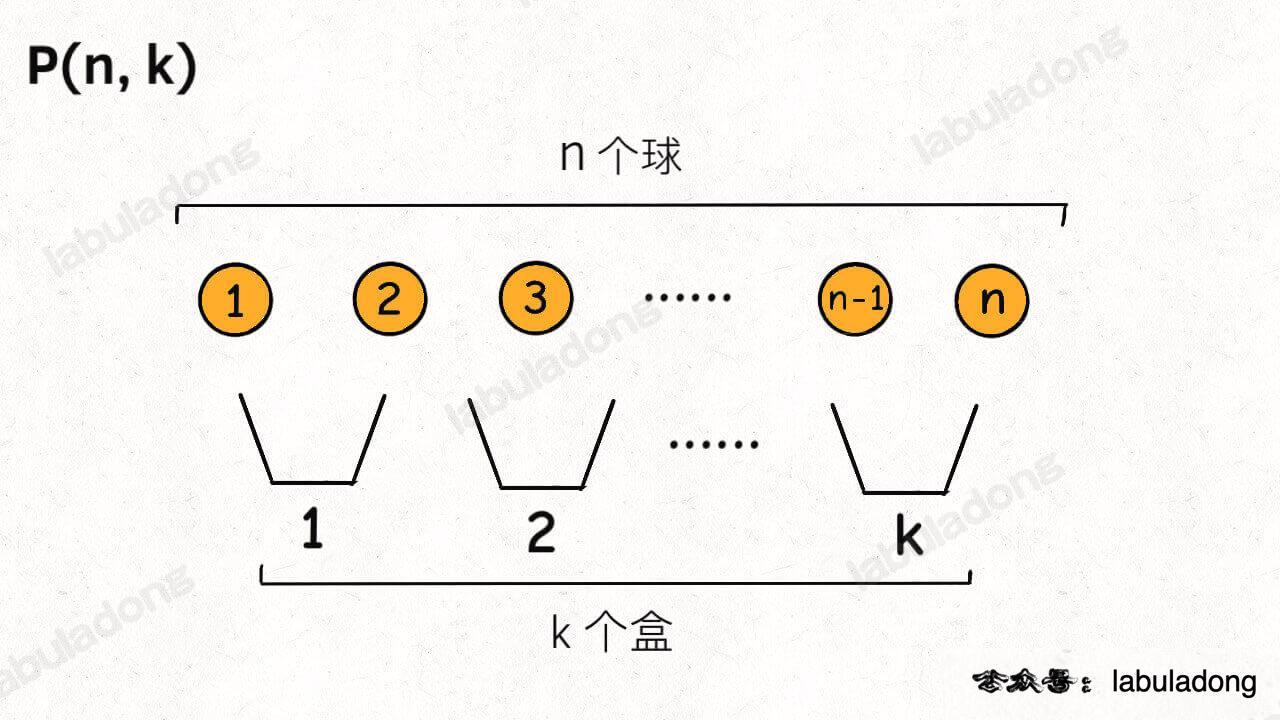
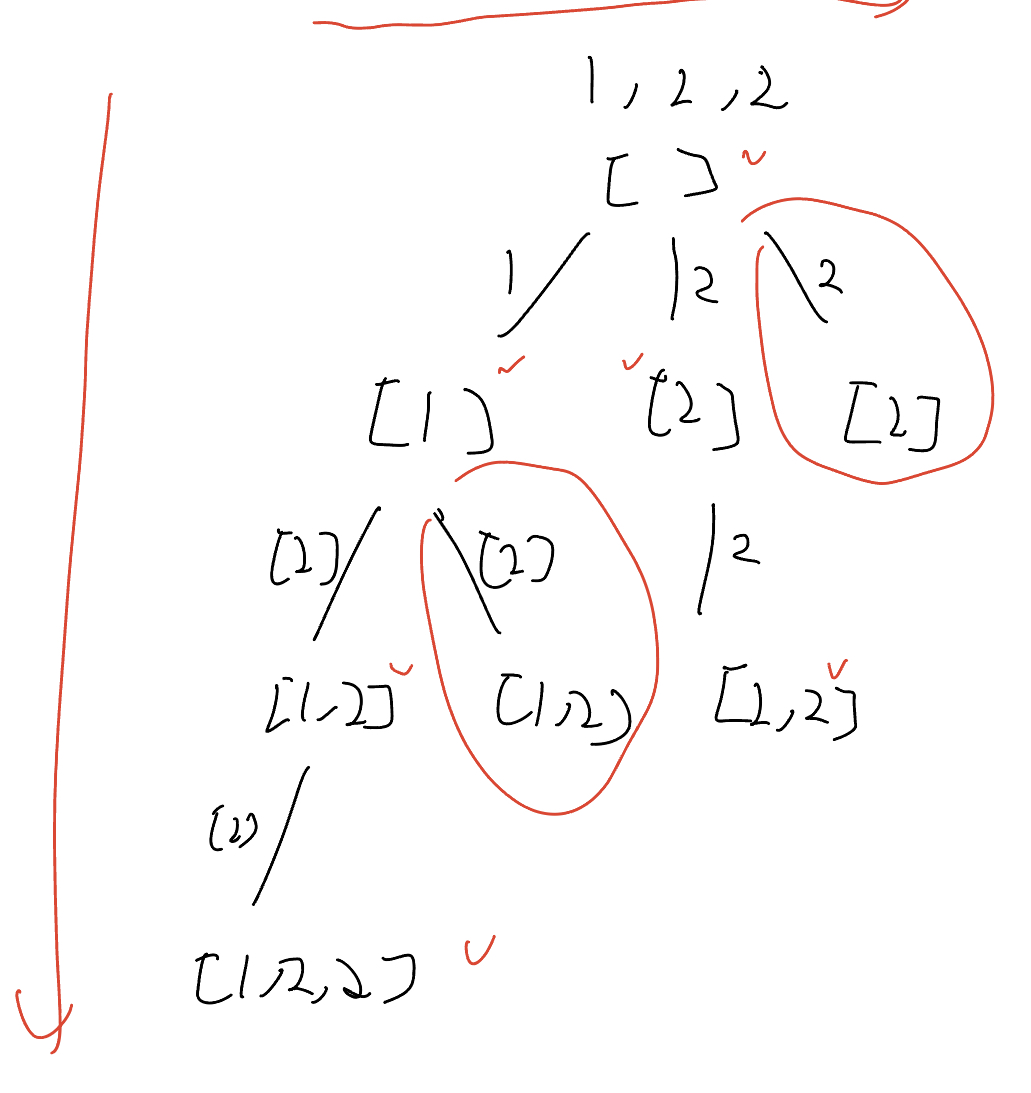综述

这类问题一般就是说 从 序列 nums 中 以给定规则取若干元素 有如下几种变体：

  1. 元素无重不可复选，即 nums 中的元素都是唯一的，每个元素最多只能被使用一次，这也是最基本的形式
    1. 以组合为例，如果输入 nums = [2,3,6,7]，和为 7 的组合应该只有 [7]。
  2. 元素可重不可复选，即 nums 中的元素可以存在重复，每个元素最多只能被使用一次。
    1. 以组合为例，如果输入 nums = [2,5,2,1,2]，和为 7 的组合应该有两种 [2,2,2,1] 和 [5,2]。
  3. 元素无重可复选，即 nums 中的元素都是唯一的，每个元素可以被使用若干次。
    1. 以组合为例，如果输入 nums = [2,3,6,7]，和为 7 的组合应该有两种 [2,2,3] 和 [7]。

PS: 也可以说有第四种形式，即元素可重可复选。但既然元素可复选，那又何必存在重复元素呢？元素去重之后就等同于形式三，所以这种情况不用考虑。

排列、组合、子集问题都可以有这三种基本形式，所以共有 9 种变化。但无论形式怎么变化，其本质就是穷举所有解，而这些解呈现树形结构，所以合理使用回溯算法框架，稍改代码框架即可把这些问题一网打尽。

回溯组合_子集树

回溯排列树

元素无重不可复选

78. 子集

lc78子集

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    LinkedList<Integer> path = new LinkedList<>();
    List<List<Integer>> res = new ArrayList<>();
    public List<List<Integer>> subsets(int[] nums) {
        int startIdx = 0;
        backtracking(nums, startIdx);
        return res;
    }

    private void backtracking(int[] nums, int startIdx) {
      	// 直接将路径加入答案中
        res.add(new LinkedList<>(path));

        for (int i = startIdx; i < nums.length; i++) {
            int cur = nums[i];
            path.add(cur);
            backtracking(nums, i + 1);
            path.removeLast();
        }
    }
}

77. 组合

lc77_组合_代码随想录

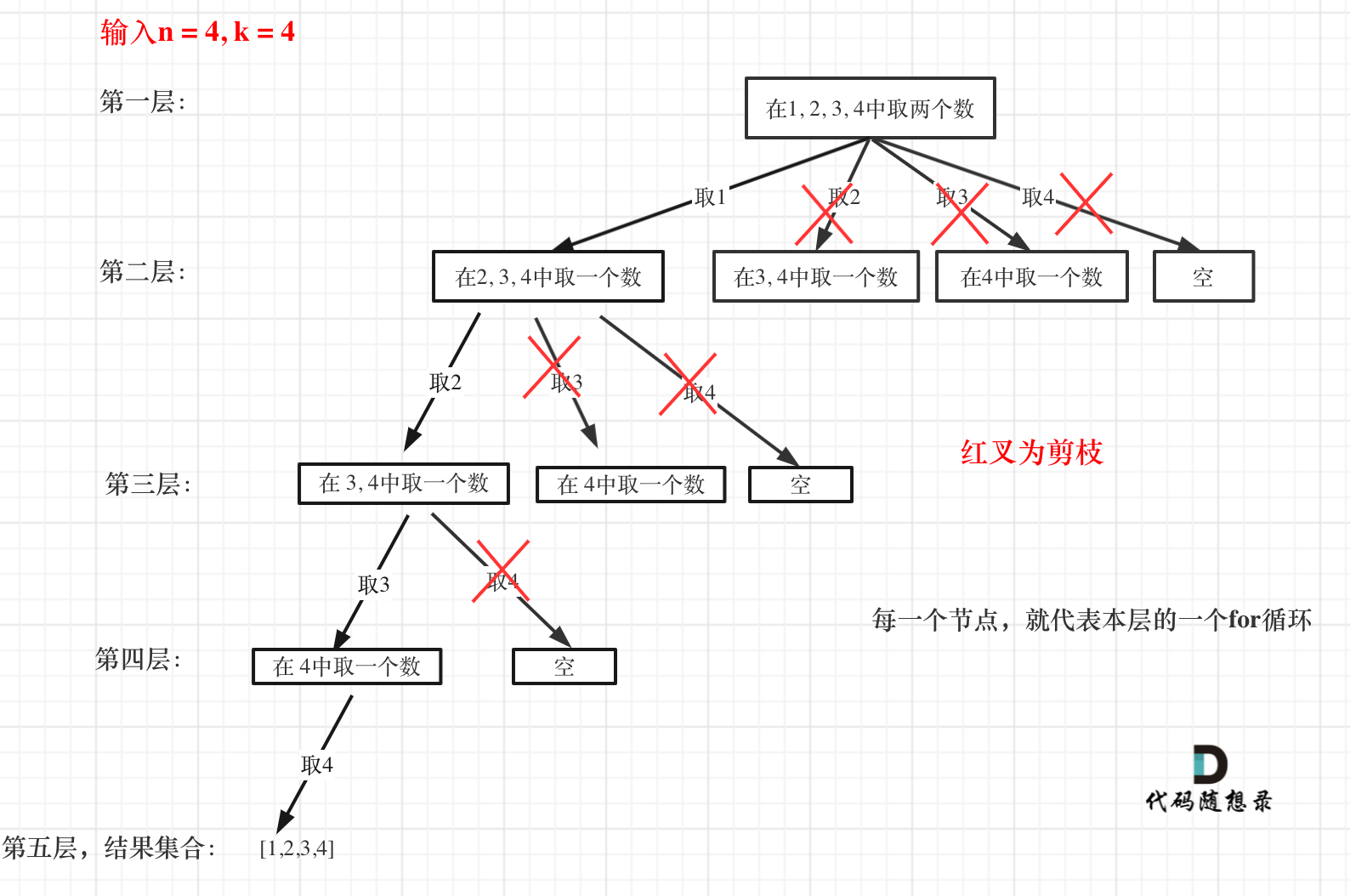
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public List<List<Integer>> combine(int n, int k) {
        List<List<Integer>> paths = new ArrayList<>();
        List<Integer> path = new ArrayList<>();
        int idx = 1;
        backtracking(idx, paths, path, n, k);
        return paths;
    }

    private void backtracking(int idx, List<List<Integer>> paths, List<Integer> path, int n, int k) {
        if (path.size() == k) {
            paths.add(new ArrayList<>(path));
            return;
        }
        for (int i = idx; i <= n; i++) {
            path.add(i);
            backtracking(i + 1, paths, path, n, k);
            path.remove(path.size() - 1);
        }
    }
}

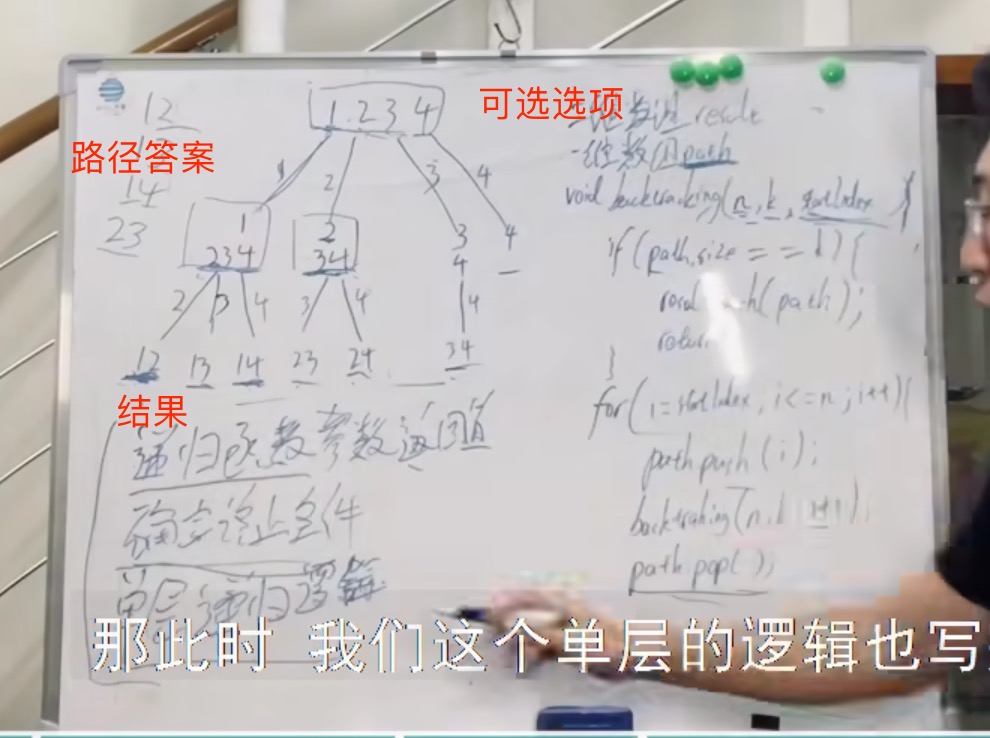
剪枝 （只需要当元素不够时剪掉即可）-> n - (k - path.size()) + 1

当所需要的元素 > 可选选项可以提供的元素时，我们就无需再往后面进行计算了，直接剪掉

组合—剪枝

优化过程如下：

  1. 已经选择的元素个数：path.size();
  2. 所需需要的元素个数为: k - path.size();
  3. 列表中剩余元素（n-i） >= 所需需要的元素个数（k - path.size()）
  4. 在集合n中至多要从该起始位置 : i <= n - (k - path.size()) + 1，开始遍历

为什么有个+1呢，因为包括起始位置，我们要是一个左闭的集合。

举个例子，n = 4，k = 3， 目前已经选取的元素为0（path.size为0），n - (k - 0) + 1 即 4 - ( 3 - 0) + 1 = 2。

从2开始搜索都是合理的，可以是组合[2, 3, 4]。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public List<List<Integer>> combine(int n, int k) {
        List<List<Integer>> paths = new ArrayList<>();
        List<Integer> path = new ArrayList<>();
        int idx = 1;
        backtracking(idx, paths, path, n, k);
        return paths;
    }

    private void backtracking(int idx, List<List<Integer>> paths, List<Integer> path, int n, int k) {
        if (path.size() == k) {
            paths.add(new ArrayList<>(path));
            return;
        }
        for (int i = idx; i <= n - (k - path.size()) + 1; i++) {
            path.add(i);
            backtracking(i + 1, paths, path, n, k);
            path.remove(path.size() - 1);
        }
    }
}

46. 全排列

全排列-路径

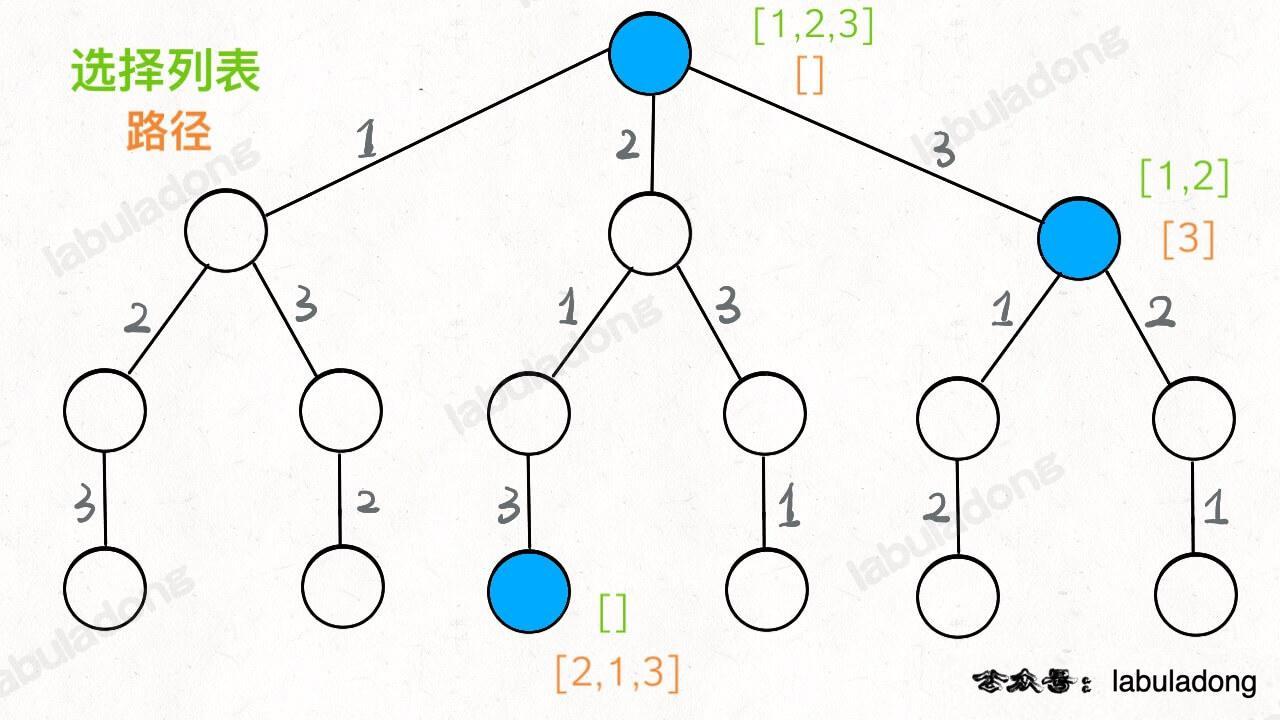
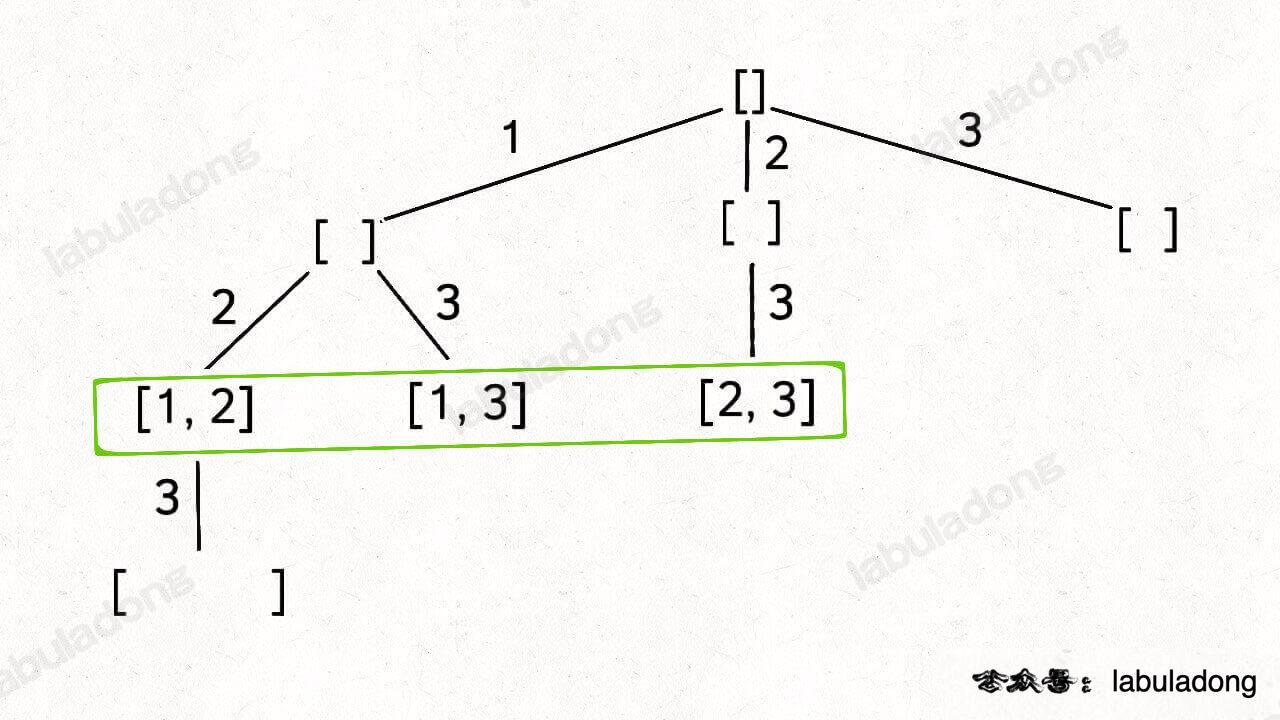
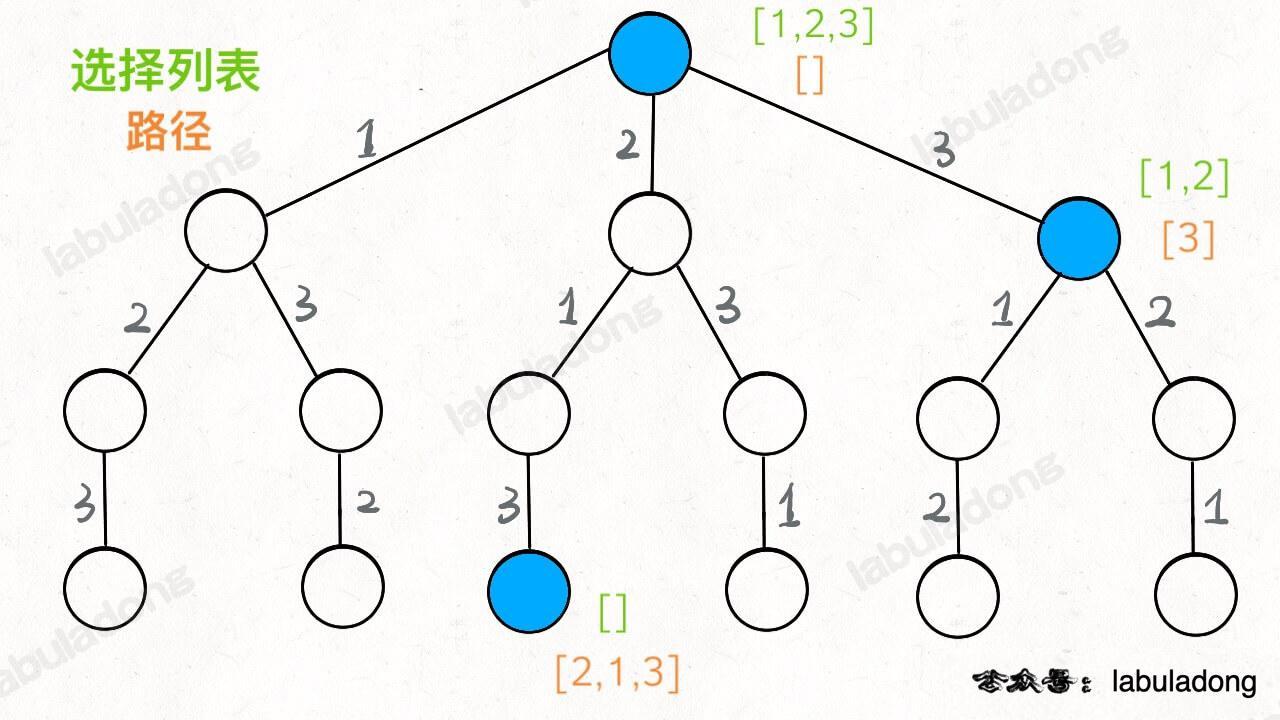
[2] 就是「路径」，记录你已经做过的选择；

[1,3] 就是「选择列表」，表示你当前可以做出的选择；

「结束条件」就是遍历到树的底层叶子节点，这里也就是选择列表为空的时候。

全排列-做选择

lc46_全排列

全排列和上边的组合和子集不同的是，我们需要左边的元素，因此不能用startIdx来避免掉重复元素，并且我们不能重复选择一个元素，那么我们就需要一个额外的数据结构来跟踪哪些值是被用过了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
    List<List<Integer>> res = new ArrayList<>();
    LinkedList<Integer> path = new LinkedList<>();
    Set<Integer> visited = new HashSet<>();
    public List<List<Integer>> permute(int[] nums) {
        backtracking(nums);
        return res;
    }

    private void backtracking(int[] nums) {
        if (path.size() == nums.length) {
            res.add(new ArrayList<>(path));
            return;
        }

        for (int i = 0; i < nums.length; i++) {
            if (visited.contains(nums[i])) continue;
            path.add(nums[i]);
            visited.add(nums[i]);
            backtracking(nums);
            path.removeLast();
            visited.remove(nums[i]);
        }
    }

}

注意hashset在这里是有局限性的因为这道题的元素不重复因此可以用hashset，但应该用boolean visited[]更通用一些：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {

    List<List<Integer>> res = new LinkedList<>();
    LinkedList<Integer> track = new LinkedList<>();
    boolean[] used;

    public List<List<Integer>> permuteUnique(int[] nums) {
        used = new boolean[nums.length];
        backtrack(nums);
        return res;
    }

    void backtrack(int[] nums) {
        if (track.size() == nums.length) {
            res.add(new LinkedList(track));
            return;
        }

        for (int i = 0; i < nums.length; i++) {
            if (used[i]) {
                continue;
            }
            track.add(nums[i]);
            used[i] = true;
            backtrack(nums);
            track.removeLast();
            used[i] = false;
        }
    }
}

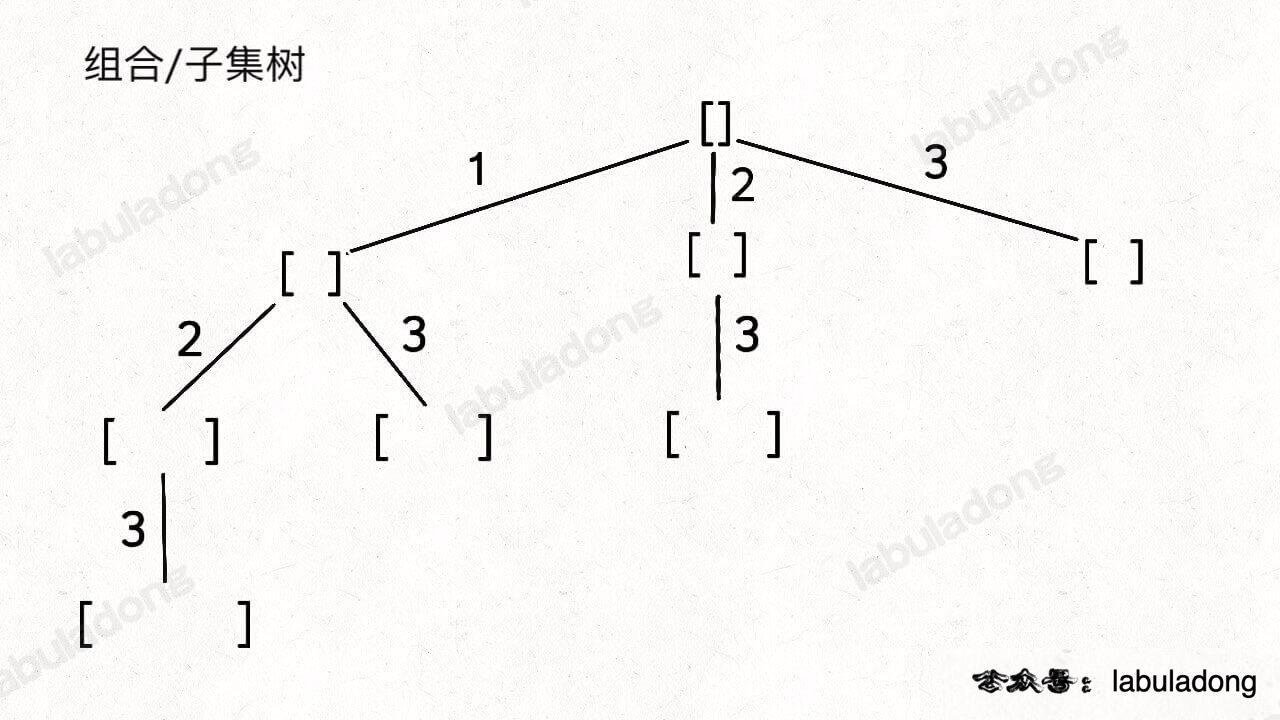
总结

子集 还是 组合：

要求大小为 2 的所有组合，就是所有大小为 2 的子集

所以 组合和子集是一样的：大小为 k 的组合就是大小为 k 的子集。

比如：

LC77：给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

就是：

给你输入一个数组 nums = [1,2..,n] 和一个正整数 k，请你生成所有大小为 k 的子集。

也就是LC78：给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的子集（幂集）。

这个组合和子集的唯一区别就是我们现在只需要输出第k层的记过，而不是在前序位置每条路径都加入

LC77_组合_labuladong

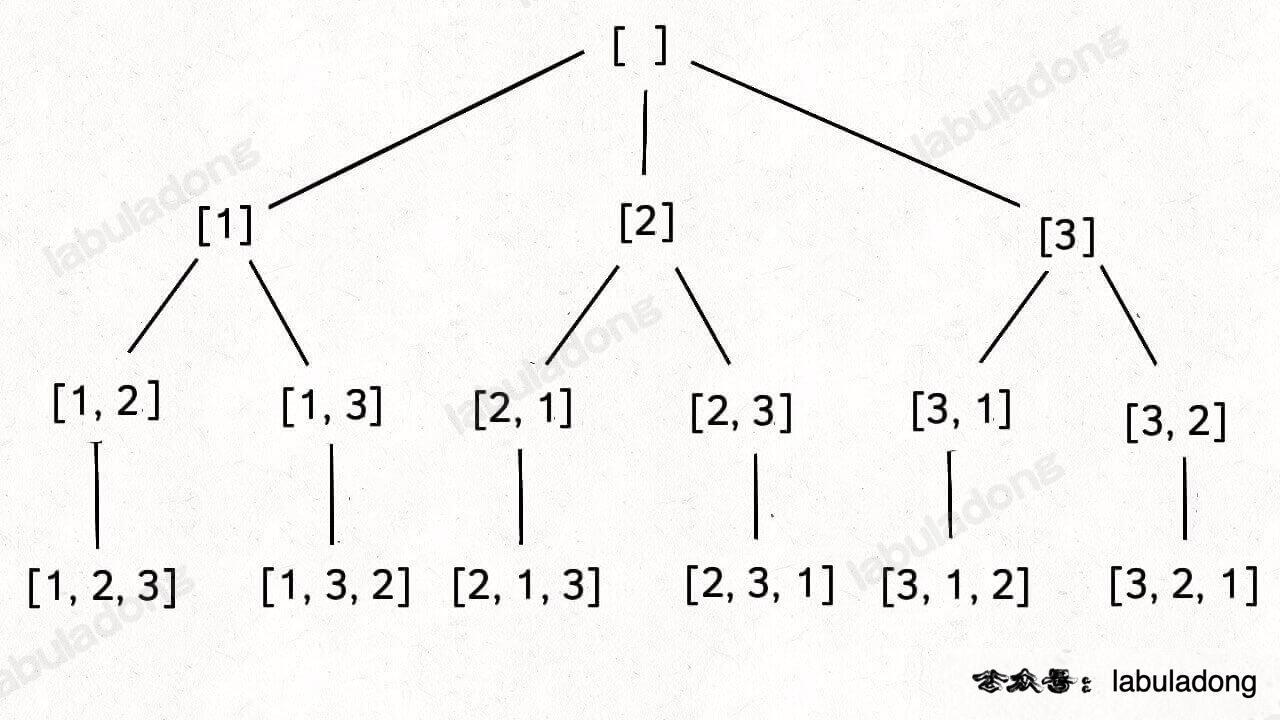
全排列的index：

排列问题本身就是让你穷举元素的位置，nums[i] 之后也可以出现 nums[i] 左边的元素，所以之前的那一套使用 startIndex 的就不行了，需要额外使用 used 数组或者hashSet来标记哪些元素还可以被选择。

如果题目不让你算全排列，而是让你算元素个数为 k 的排列，怎么算？也很简单，改下 backtrack 函数的 base case，仅收集第 k 层的节点值即可：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
// 回溯算法核心函数
void backtrack(int[] nums, int k) {
    // base case，到达第 k 层，收集节点的值
    if (track.size() == k) {
        // 第 k 层节点的值就是大小为 k 的排列
        res.add(new LinkedList(track));
        return;
    }

    // 回溯算法标准框架
    for (int i = 0; i < nums.length; i++) {
        // ...
        backtrack(nums, k);
        // ...
    }
}

元素可重不可复选

90. 子集 II

lc90_subset2_tree

如图中所示，我们可以看到的是，同一层的相邻元素如果相同，我们就不需要再处理。

为了保证相邻元素是相同的我们就需要用一个sort

综上我们有：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    List<List<Integer>> res = new ArrayList<>();
    LinkedList<Integer> path = new LinkedList<>();

    public List<List<Integer>> subsetsWithDup(int[] nums) {
      	// 排序来保证相邻元素一定是相同的（如果有的话）
        Arrays.sort(nums);
        backtracking(nums, 0);
        return res;
    }

    private void backtracking(int[] nums, int startIdx) {
        res.add(new LinkedList<>(path));
        for (int i = startIdx; i < nums.length; i++) {
            // 注意这里的剪枝逻辑
            if (i > startIdx && nums[i] == nums[i - 1]) {
                continue;
            }
            path.addLast(nums[i]);
            backtracking(nums, i + 1);
            path.removeLast();
        }
    }
}

40. 组合总和 II

子集问题就是组合的一种问题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {

    List<List<Integer>> res = new ArrayList<>();
    LinkedList<Integer> path = new LinkedList<>();
    int curSum = 0;

    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        Arrays.sort(candidates);
        backtracking(candidates, target, 0);
        return res;
    }

    private void backtracking(int[] candidates, int target, int startIdx) {
        if (curSum == target) {
            res.add(new LinkedList<>(path));
            return;
        }

        // 进行额外的剪枝，否则会超时
        if (curSum > target) return;

        for (int i = startIdx; i < candidates.length; i++) {
            if (i > startIdx && candidates[i] == candidates[i - 1]) continue;
            curSum += candidates[i];
            path.add(candidates[i]);
            backtracking(candidates, target, i + 1);
            path.removeLast();
            curSum -= candidates[i];
        }
    }
}

47. 全排列 II

  1. 用used数组来跟踪哪些数在递归（向下生长时）被用过，从而避免重复
  2. i > 0 && nums[i - 1] == nums[i] && !used[i - 1]
    1. 主要是用来判断当前的数和之前是否相同，如果相同且之前在同一层时候处理过，那么我们不需要再处理一遍，跳过即可
    2. 其实核心就是 保证相同元素在排列中的相对位置保持不变。
    3. 效果： 当出现重复元素时，比如输入 nums = [1,2,2',2'']，2' 只有在 2 已经被使用的情况下才会被选择，同理，2'' 只有在 2' 已经被使用的情况下才会被选择，这就保证了相同元素在排列中的相对位置保证固定。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
    LinkedList<Integer> path = new LinkedList<>();
    List<List<Integer>> res = new ArrayList<>();
    boolean[] used;
    public List<List<Integer>> permuteUnique(int[] nums) {
        used = new boolean[nums.length];
        Arrays.sort(nums);
        backtracking(nums);
        return res;
    }

    private void backtracking(int[] nums) {
        if (nums.length == path.size()) {
            res.add(new ArrayList<>(path));
            return;
        }

        for (int i = 0; i < nums.length; i++) {
            if (used[i]) continue;
            if (i > 0 && nums[i - 1] == nums[i] && !used[i - 1]) {
                // 这里的 nums[i - 1] == nums[i] && !used[i - 1]
                // 主要是为了说明现在出现了一个新的和之前一样的数，那么由于之前已经计算过，现在已经不需要重复算了
                continue;
            }
            path.addLast(nums[i]);
            used[i] = true;
            backtracking(nums);
            path.removeLast();
            used[i] = false;
        }
    }
}

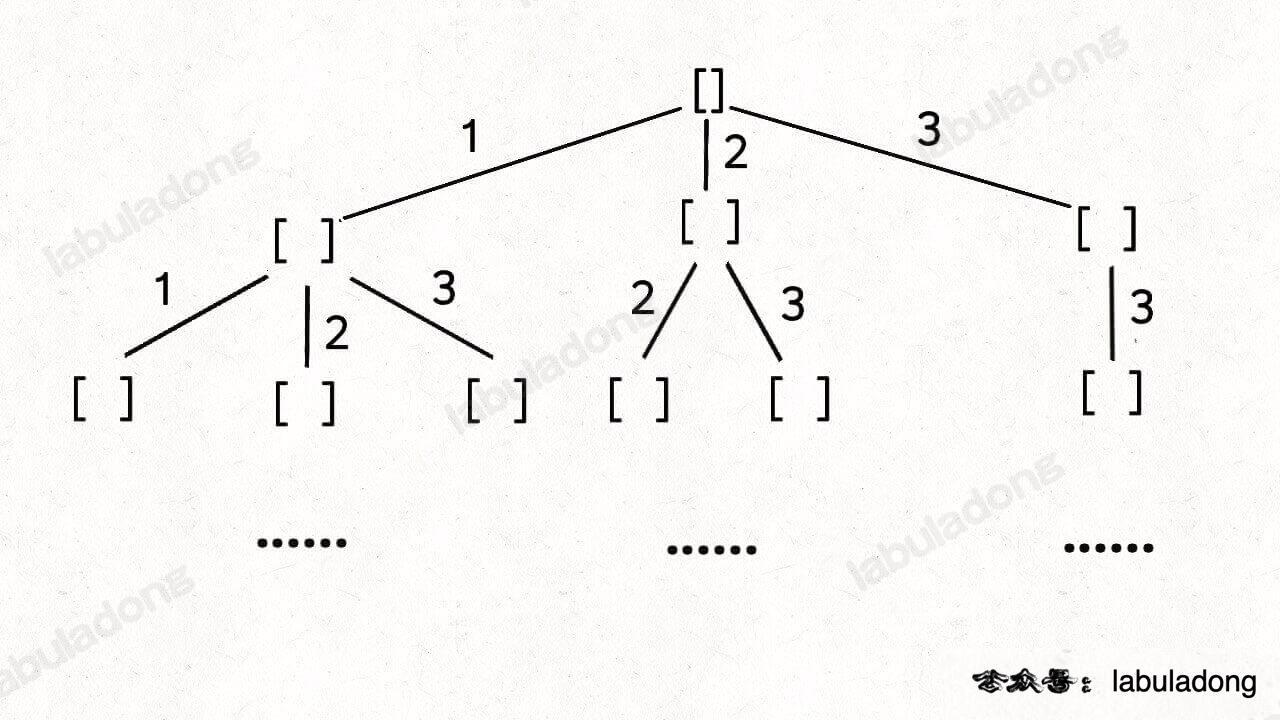
元素无重可复选

39. 组合总和

对于之前的解法我们是 startIdx 每一次传入i + 1 那么下一层回溯树就是从 i + 1 开始，从而保证当前元素不会被重复使用：

lc_子集不可重复

对于本题来说，其实就是修改了startIdx 之前是 i + 1 现在是 i

相当于给之前的回溯树添加了一条树枝，在遍历这棵树的过程中，一个元素可以被无限次使用：

lc39_tree

⚠️ 需要注意的是，这样会导致树无限生长，因此我们还需要额外的base case 来结束递归: if (curSum > target) return; 即路径和大于 target 时就没必要再遍历下去了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
    LinkedList<Integer> path = new LinkedList<>();
    List<List<Integer>> res = new ArrayList<>();
    int curSum = 0;
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        backtracking(candidates, target, 0);
        return res;
    }

    private void backtracking(int[] candidates, int target, int startIdx) {
        if (curSum == target) {
            res.add(new LinkedList<>(path));
            return;
        }

        if (curSum > target) return;

        for (int i = startIdx; i < candidates.length; i++) {
            curSum += candidates[i];
            path.addLast(candidates[i]);
            backtracking(candidates, target, i);
            curSum -= candidates[i];
            path.removeLast();
        }
    }
}

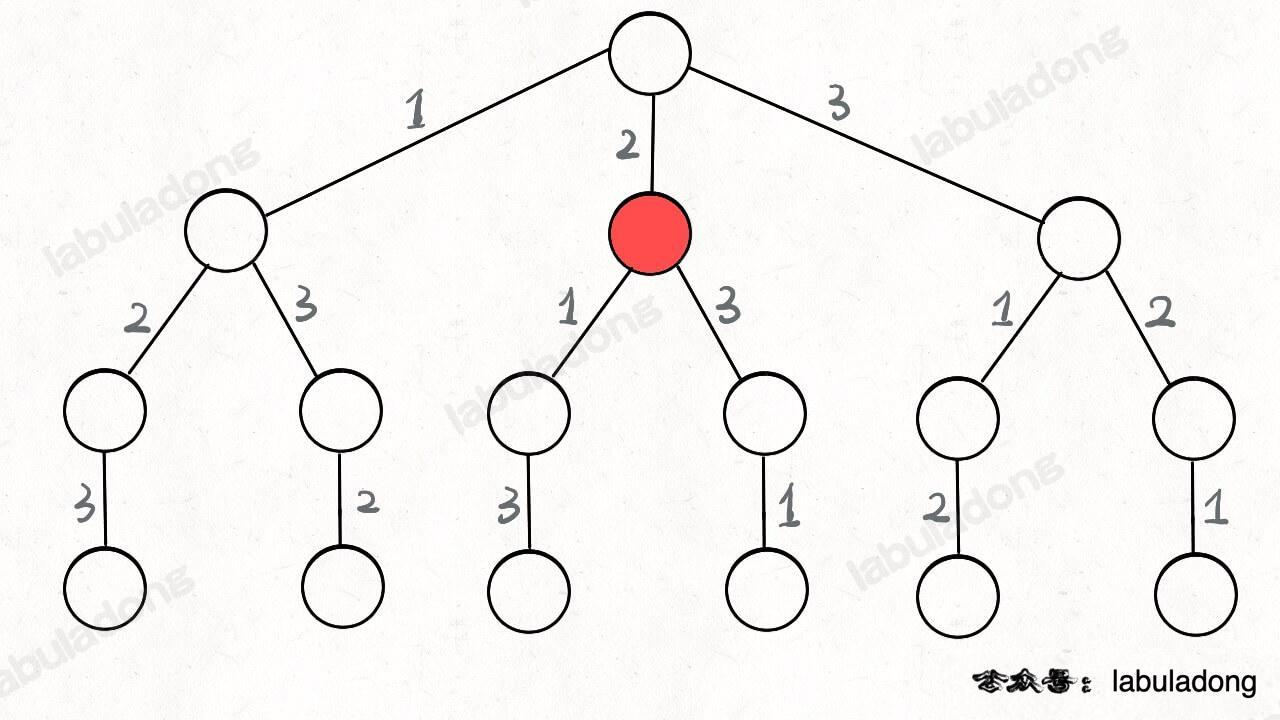
排列

力扣上没有类似的题目，我们不妨先想一下，nums 数组中的元素无重复且可复选的情况下，会有哪些排列？

比如输入 nums = [1,2,3]，那么这种条件下的全排列共有 3^3 = 27 种：

标准的全排列算法利用 used 数组进行剪枝，避免重复使用同一个元素。如果允许重复使用元素的话，直接放飞自我，去除所有 used 数组的剪枝逻辑就行了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {

    List<List<Integer>> res = new LinkedList<>();
    LinkedList<Integer> track = new LinkedList<>();

    public List<List<Integer>> permuteRepeat(int[] nums) {
        backtrack(nums);
        return res;
    }

    // 回溯算法核心函数
    void backtrack(int[] nums) {
        // base case，到达叶子节点
        if (track.size() == nums.length) {
            // 收集叶子节点上的值
            res.add(new LinkedList(track));
            return;
        }

        // 回溯算法标准框架
        for (int i = 0; i < nums.length; i++) {
            // 做选择
            track.add(nums[i]);
            // 进入下一层回溯树
            backtrack(nums);
            // 取消选择
            track.removeLast();
        }
    }
}

总结

有很多的共性，其实树都是差不多的只是多了一些剪枝操作以及base case略有不同

元素无重不可复选

即 nums 中的元素都是唯一的，每个元素最多只能被使用一次

对于组合或者子集问题：

1
2
3
4
5
6
7
8
9
10
11
12
/* 组合/子集问题回溯算法框架 */
void backtrack(int[] nums, int start) {
    // 回溯算法标准框架
    for (int i = start; i < nums.length; i++) {
        // 做选择
        track.addLast(nums[i]);
        // 注意参数
        backtrack(nums, i + 1);
        // 撤销选择
        track.removeLast();
    }
}

对于排列问题：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
/* 排列问题回溯算法框架 */
void backtrack(int[] nums) {
    for (int i = 0; i < nums.length; i++) {
        // 剪枝逻辑
        if (used[i]) {
            continue;
        }
        // 做选择
        used[i] = true;
        track.addLast(nums[i]);

        backtrack(nums);
        // 撤销选择
        track.removeLast();
        used[i] = false;
    }
}

元素可重不可复选

即 nums 中的元素可以存在重复，每个元素最多只能被使用一次，其关键在于排序和剪枝，backtrack 核心代码如下：

对于组合或者子集问题：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
Arrays.sort(nums);
/* 组合/子集问题回溯算法框架 */
void backtrack(int[] nums, int start) {
    // 回溯算法标准框架
    for (int i = start; i < nums.length; i++) {
        // 剪枝逻辑，跳过值相同的相邻树枝
        if (i > start && nums[i] == nums[i - 1]) {
            continue;
        }
        // 做选择
        track.addLast(nums[i]);
        // 注意参数
        backtrack(nums, i + 1);
        // 撤销选择
        track.removeLast();
    }
}

对于排列问题：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
Arrays.sort(nums);
/* 排列问题回溯算法框架 */
void backtrack(int[] nums) {
    for (int i = 0; i < nums.length; i++) {
        // 剪枝逻辑
        if (used[i]) {
            continue;
        }
        // 剪枝逻辑，固定相同的元素在排列中的相对位置
        if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) {
            continue;
        }
        // 做选择
        used[i] = true;
        track.addLast(nums[i]);

        backtrack(nums);
        // 撤销选择
        track.removeLast();
        used[i] = false;
    }
}

元素无重可复选

即 nums 中的元素都是唯一的，每个元素可以被使用若干次，只要删掉去重逻辑即可，backtrack 核心代码如下：

对于组合或者子集问题：

1
2
3
4
5
6
7
8
9
10
11
12
/* 组合/子集问题回溯算法框架 */
void backtrack(int[] nums, int start) {
    // 回溯算法标准框架
    for (int i = start; i < nums.length; i++) {
        // 做选择
        track.addLast(nums[i]);
        // 注意参数
        backtrack(nums, i);
        // 撤销选择
        track.removeLast();
    }
}

对于排列问题：

1
2
3
4
5
6
7
8
9
10
/* 排列问题回溯算法框架 */
void backtrack(int[] nums) {
    for (int i = 0; i < nums.length; i++) {
        // 做选择
        track.addLast(nums[i]);
        backtrack(nums);
        // 撤销选择
        track.removeLast();
    }
}

其他例题

组合

216. 组合总和 III

和77题几乎一模一样

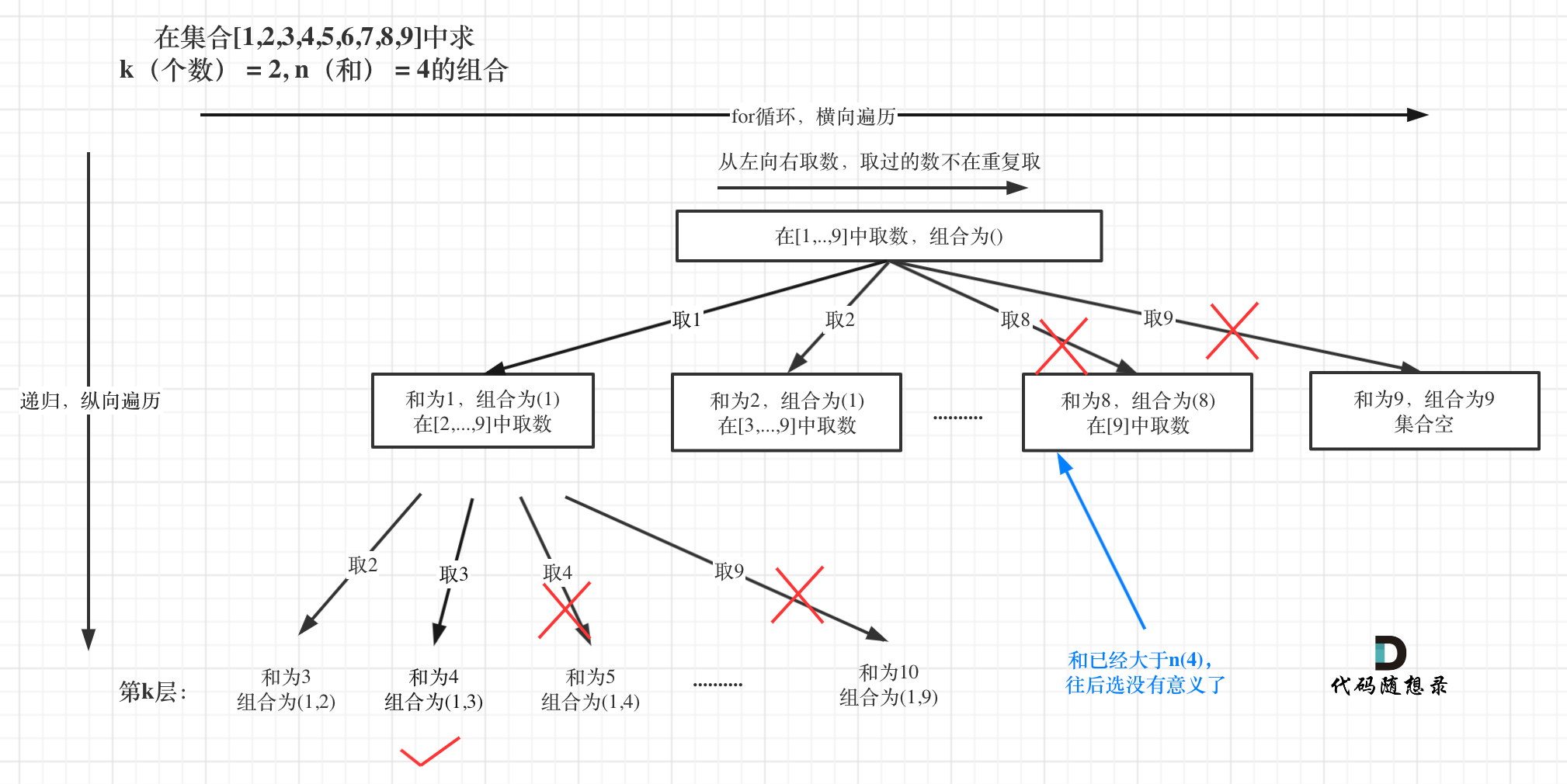
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
    int curSum = 0;
    public List<List<Integer>> combinationSum3(int k, int n) {
        List<Integer> path = new ArrayList<>();
        List<List<Integer>> paths = new ArrayList<>();
        backTracking(path, paths, k, n, 1);
        return paths;
    }

    private void backTracking(List<Integer> path, List<List<Integer>> paths, int k, int n, int startIdx) {
        if (path.size() == k) {
            if (curSum == n) {
                paths.add(new ArrayList<>(path));
            }
            return;
        }

        for (int i = startIdx; i <= 9; i++) {
            path.add(i);
            curSum += i;
            backTracking(path, paths, k, n, i + 1);
            path.remove(path.size() - 1);
            curSum -= i;
        }
    }
}

剪枝

这道题剪枝有两个： 剩余元素的剪枝 + 求和的剪枝

剩余元素的剪枝:

即，可选列表中的元素 < 要用的元素

求和的剪枝：

即，当前和已经大于了题目要求的和

组合总和3-剪枝

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
    int curSum = 0;
    public List<List<Integer>> combinationSum3(int k, int n) {
        List<Integer> path = new ArrayList<>();
        List<List<Integer>> paths = new ArrayList<>();
        backTracking(path, paths, k, n, 1);
        return paths;
    }

    private void backTracking(List<Integer> path, List<List<Integer>> paths, int k, int n, int startIdx) {
        if (path.size() == k) {
            if (curSum == n) {
                paths.add(new ArrayList<>(path));
            }
            return;
        }

        for (int i = startIdx; i <= 9 - (k - path.size()) + 1; i++) {
            path.add(i);
            curSum += i;
            if (curSum > n) {
                curSum -= i;
                path.remove(path.size() - 1);
                return;
            }
            backTracking(path, paths, k, n, i + 1);
            path.remove(path.size() - 1);
            curSum -= i;
        }
    }
}

17. 电话号码的字母组合

组合的应用题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
        Map<Character, String> phoneMap = new HashMap<>();
        public List<String> letterCombinations(String digits) {
            phoneMap.put('2', "abc");
            phoneMap.put('3', "def");
            phoneMap.put('4', "ghi");
            phoneMap.put('5', "jkl");
            phoneMap.put('6', "mno");
            phoneMap.put('7', "pqrs");
            phoneMap.put('8', "tuv");
            phoneMap.put('9', "wxyz");
            List<String> res = new LinkedList<>();
            StringBuilder cur = new StringBuilder();
            int idx = 0;
            backtracking(digits, cur, res, idx);
            return res;
        }

        private void backtracking(String digits, StringBuilder cur, List<String> res, int idx) {
            if (idx > digits.length() - 1) {
                res.add(cur.toString());
                return;
            }
            char digit = digits.charAt(idx);
            String digit2Chars = phoneMap.get(digit);
            for (int i = 0; i < digit2Chars.length(); i++) {
                char target = digit2Chars.charAt(i);
                cur.append(target);
                backtracking(digits, cur, res, idx + 1);
                cur.deleteCharAt(cur.length() - 1);
            }
        }
    }

子集

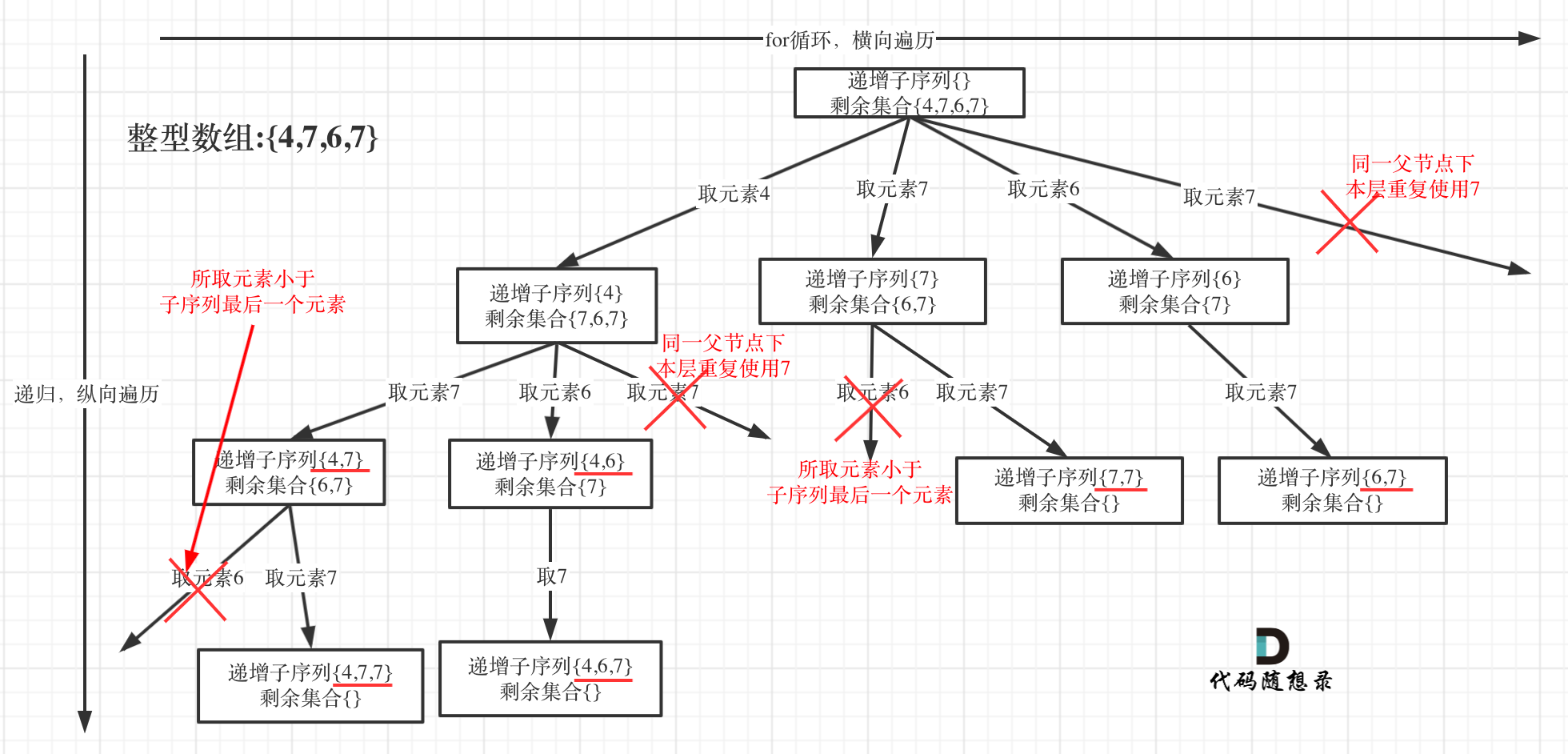
491. 递增子序列

首先 本题在寻找 递增子序列 因此本题相当于寻找一种特殊的子集，特殊的地方在于 子集中的元素是递增的

但是相较于子集问题（特指 90.子集2）本题特殊点在于我们不能再通过排序来过滤掉重复元素，因为这会破坏数组原本的顺序。

因此我们需要一个 hashset 来帮助我们寻找哪些元素在本层中用过，注意这里只需要看本层：

491_递增子序列_tree

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
    LinkedList<Integer> path = new LinkedList<>();
    List<List<Integer>> res = new ArrayList<>();

    public List<List<Integer>> findSubsequences(int[] nums) {
        backtracking(nums, 0);
        return res;
    }

    private void backtracking(int[] nums, int startIdx) {
        if (path.size() >= 2) {
            res.add(new LinkedList<>(path));
        }

        Set<Integer> used = new HashSet<>();

        for (int i = startIdx; i < nums.length; i++) {
            if (!path.isEmpty() && path.getLast() > nums[i]) {
                continue;
            }
            if (used.contains(nums[i])) {
                continue;
            }
            path.addLast(nums[i]);
            used.add(nums[i]);

            backtracking(nums, i + 1);

            path.removeLast();
        }
    }
}

为什么回溯前 used.add(nums[i]); 回溯后没有撤销？

因为 used 是记录本层元素是否重复使用，新的一层used都会重新定义（清空），所以要知道used只负责本层！