51. N 皇后

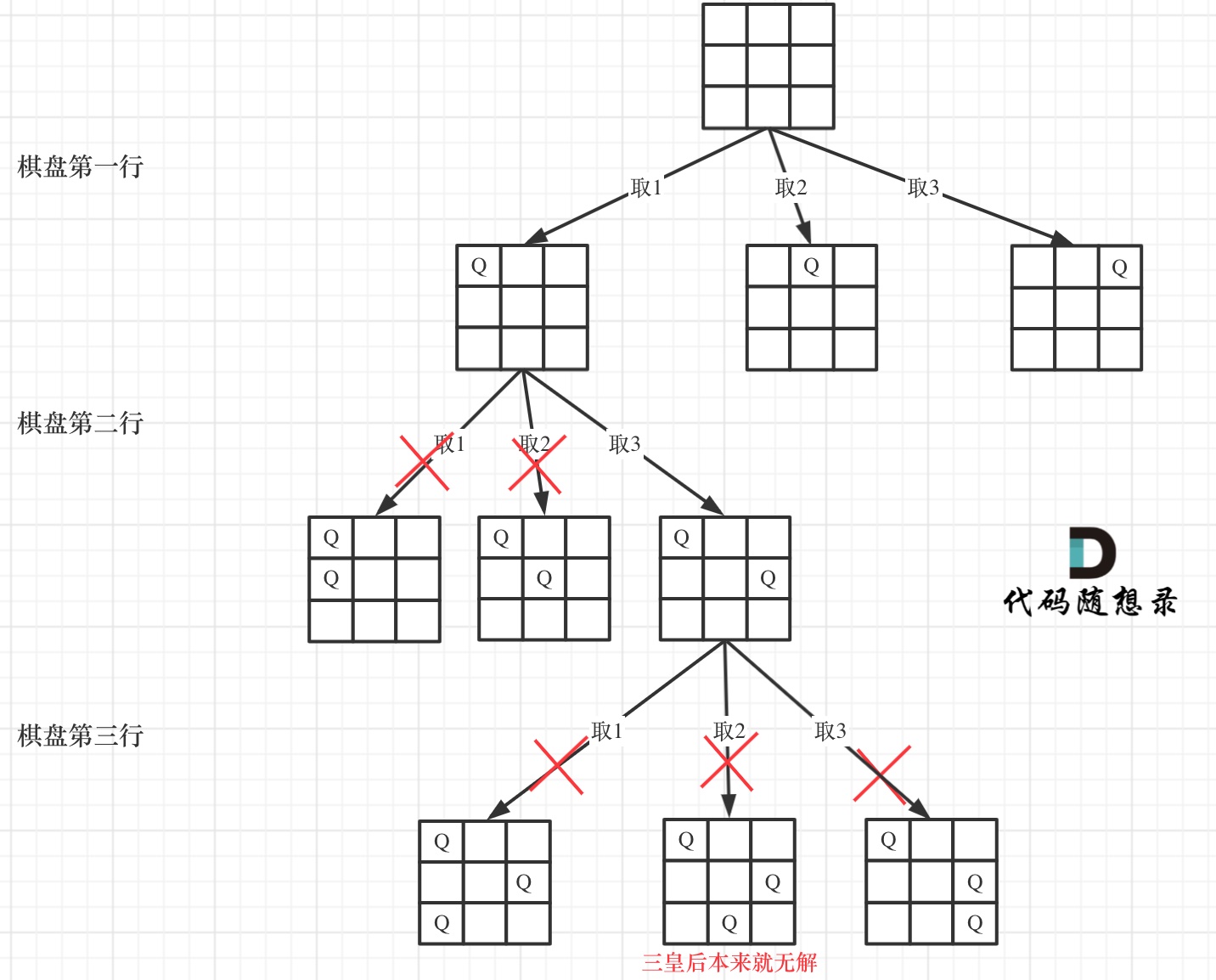
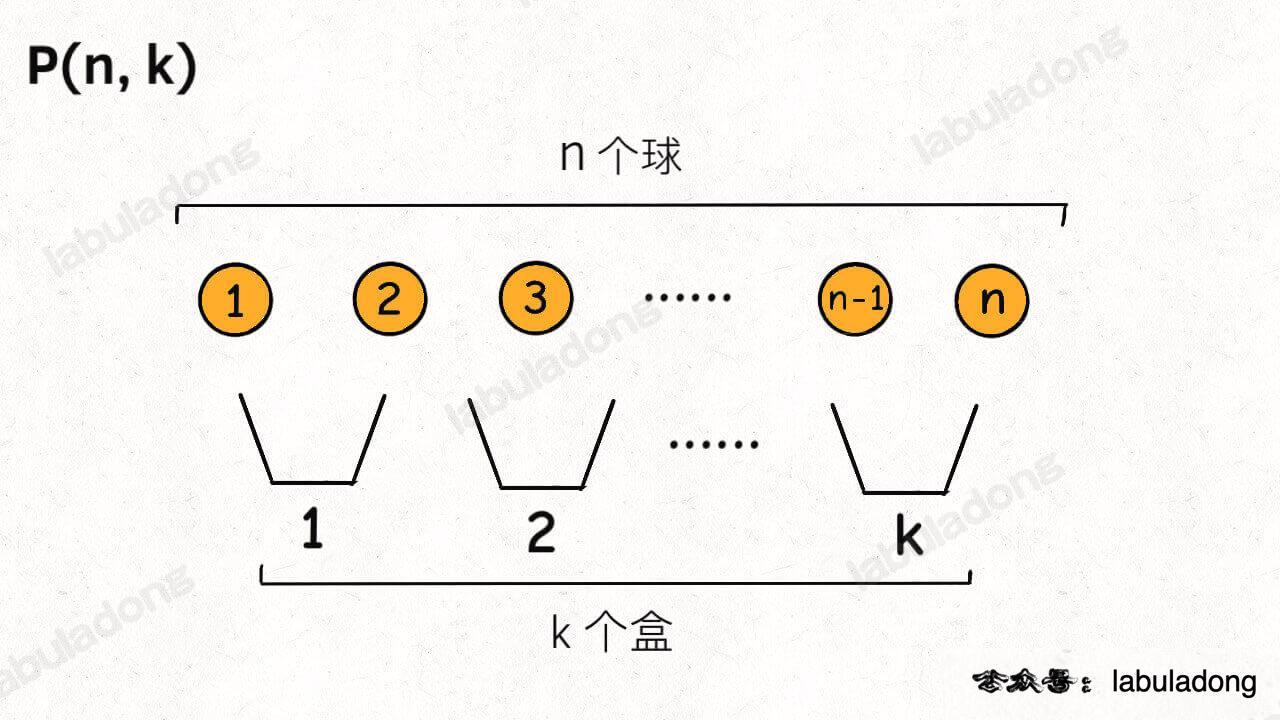
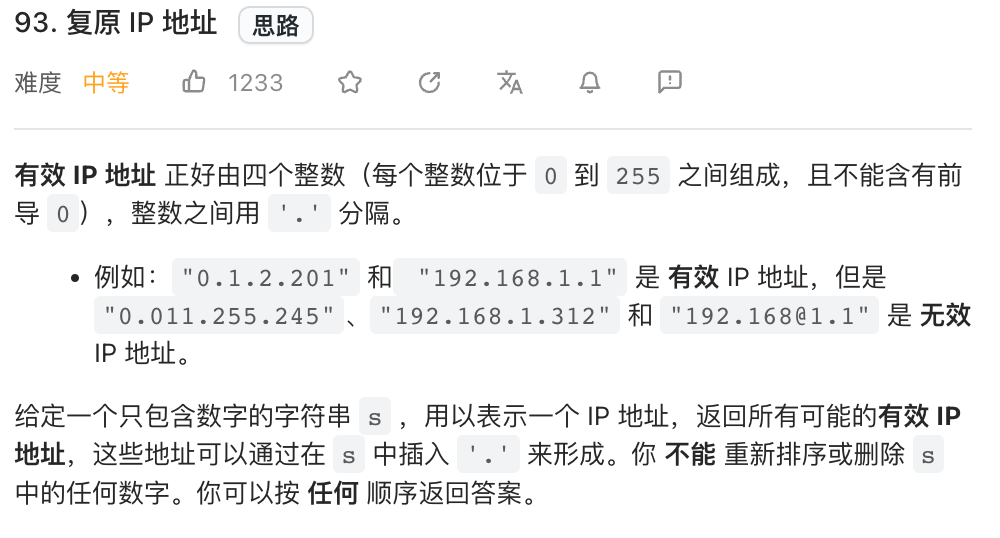
  1. 构造树：

一个 3 * 3 的棋盘，将搜索过程抽象为一棵树

二维矩阵中矩阵的高就是这棵树的高度，矩阵的宽就是树形结构中每一个节点的宽度。

那么我们用皇后们的约束条件，来回溯搜索这棵树，只要搜索到了树的叶子节点，说明就找到了皇后们的合理位置了

  1. 皇后的位置：
    1. 不能同行
    2. 不能同列
    3. 不能同斜线

51_NQueen_tree

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
class Solution {
  List<List<String>> res = new ArrayList<>();
  public List<List<String>> solveNQueens(int n) {
      char[][] chessBoard = new char[n][n];

      for (char[] chessRow : chessBoard) {
          Arrays.fill(chessRow, '.');
      }

      int curRow = 0;
      backtracking(chessBoard, curRow, n);
      return res;
  }

  private void backtracking(char[][] chessBoard, int curRow, int n) {
      if (curRow == n) {
          // 到叶子结点，将此时的棋盘加入答案
          res.add(array2List(chessBoard));
          return;
      }

      for (int curCol = 0; curCol < n; curCol++) {
          if (isValid(chessBoard, curRow, curCol)) {
              chessBoard[curRow][curCol] = 'Q';
              backtracking(chessBoard, curRow + 1, n);
              chessBoard[curRow][curCol] = '.';
          }
      }
  }

  private boolean isValid(char[][] chessBoard, int curRow, int curCol) {
      // 检查同一列是不是已经有Queen
      for (int r = 0; r < curRow; r++) {
          if (chessBoard[r][curCol] == 'Q') return false;
      }

      // 检查 \ 是否有Queen
      for (int r = curRow - 1, c = curCol - 1; r >= 0 && c >= 0; r--, c--) {
          if (chessBoard[r][c] == 'Q') return false;
      }

      // 检查 / 是否有Queen
      for (int r = curRow - 1, c = curCol + 1; r >= 0 && c < chessBoard[0].length; r--, c++) {
          if (chessBoard[r][c] == 'Q') return false;
      }
      return true;
  }


  private List<String> array2List(char[][] chessBoard) {
      List<String> transformedArray = new ArrayList<>();
      int r = chessBoard.length, c = chessBoard[0].length;

      for (char[] chars : chessBoard) {
          StringBuilder sb = new StringBuilder();
          for (int j = 0; j < c; j++) {
              sb.append(chars[j]);
          }
          transformedArray.add(sb.toString());
      }

      return transformedArray;
  }
}

37. 解数独

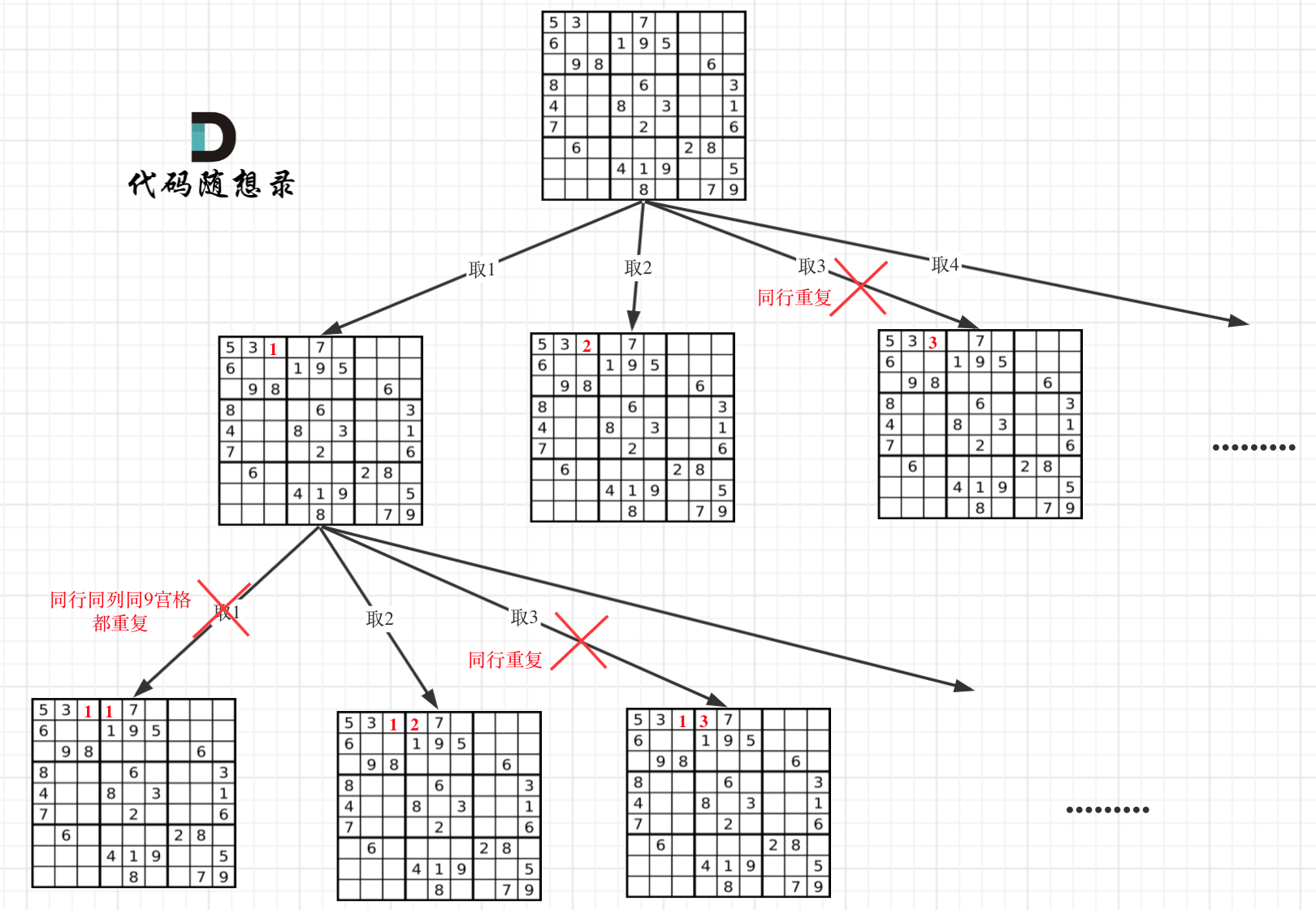
和N皇后不同的是，N皇后一旦确定某行中的位置，那么他就唯一确定了但是数独中数字会取决于之前的数字，会存在依赖关系，因此需要枚举每一个格子。

lc37_tree

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
class Solution {
    int boardRow = 9, boardCol = 9;
    public void solveSudoku(char[][] board) {
        backtracking(board, 0, 0);
    }

    private boolean backtracking(char[][] board, int r, int c) {
        if (c == boardCol) {
            return backtracking(board, r + 1, 0);
        }

        if (r == boardRow) {
            return true;
        }

        if (board[r][c] != '.') {
            return backtracking(board, r, c + 1);
        }

        for (char num = '1'; num <= '9'; num++) {
            if (!isValid(board, r, c, num)) continue;
            board[r][c] = num;
            if (backtracking(board, r, c + 1)) return true;
            board[r][c] = '.';
        }
        return false;
    }

    private boolean isValid(char[][] board, int r, int c, char num) {
        for (int i = 0; i < 9; i++) {
            // 判断行是否存在重复
            if (board[r][i] == num) return false;
            // 判断列是否存在重复
            if (board[i][c] == num) return false;
            // 判断 3 x 3 方框是否存在重复
            if (board[(r/3)*3 + i/3][(c/3)*3 + i%3] == num)
                return false;
        }
        return true;
    }
}