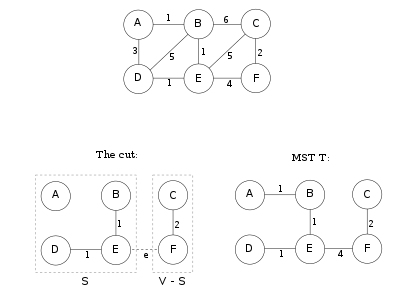
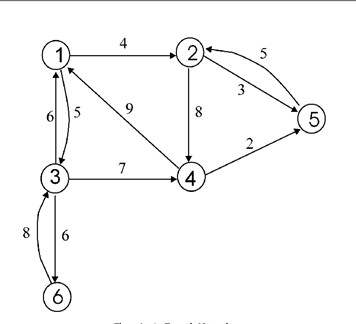
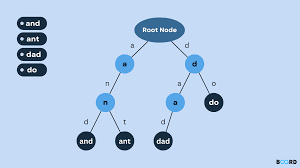
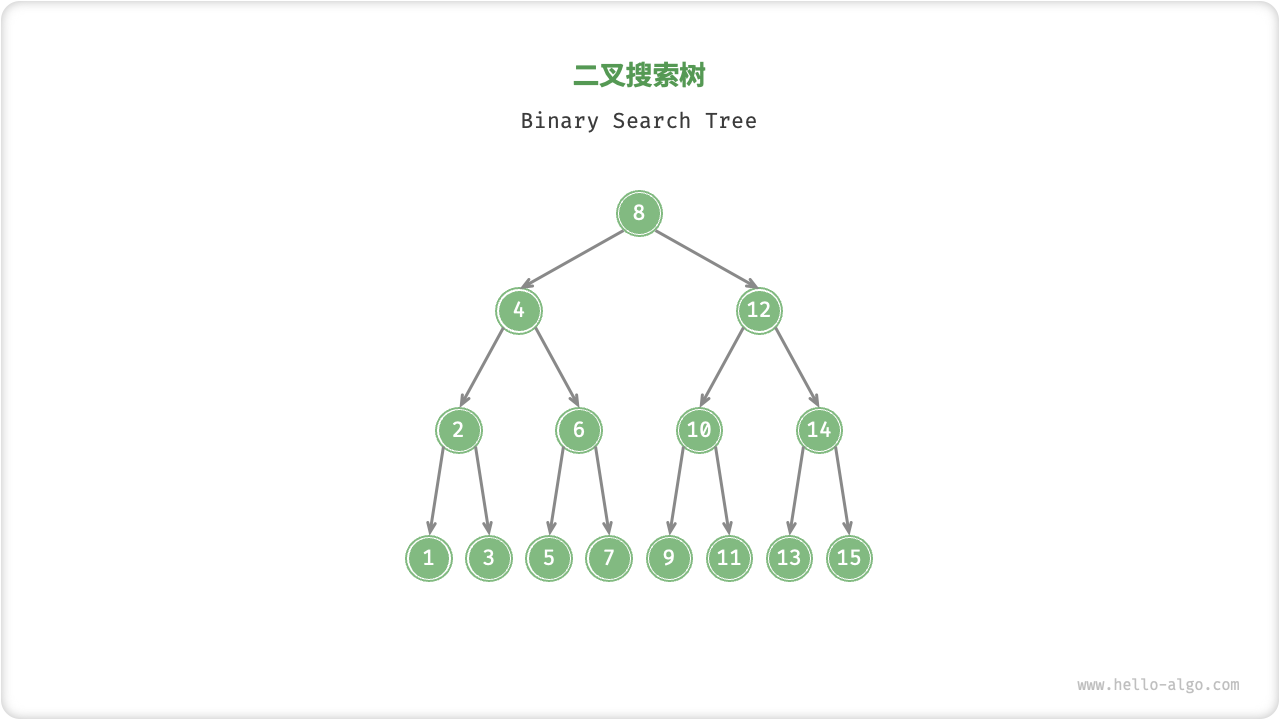
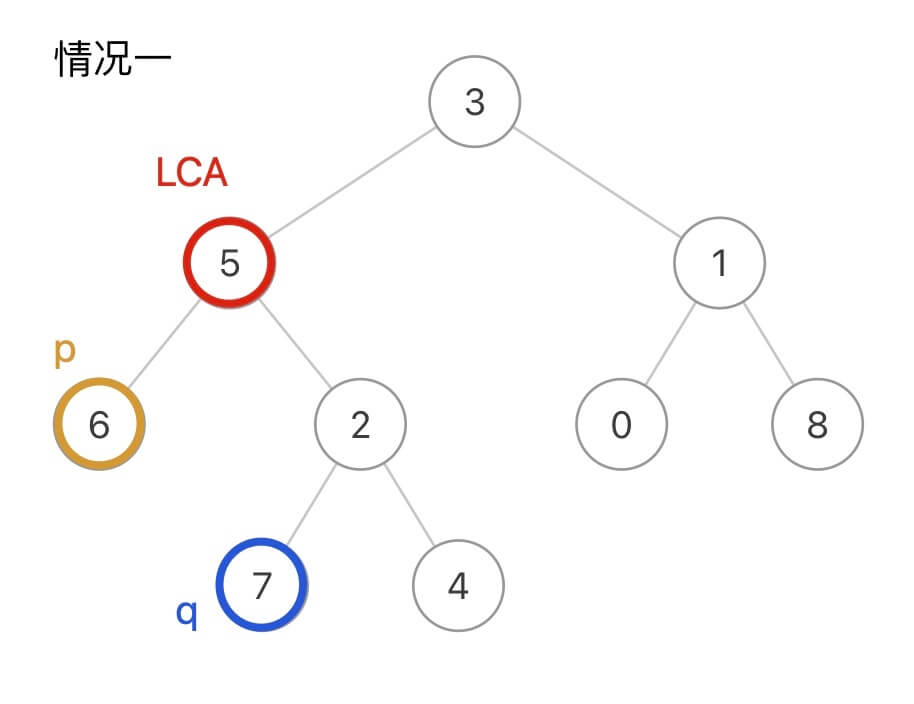
并查集 - 解决的问题
快速的支持以下的操作:(近乎 O(1))
- 将两个集合合并
- 询问两个元素是否在一个集合当中
基本原理: 每一个集合都用一颗树来表示。树根的标号就是整个集合的编号。每个节点存储他的父节点, p[x] 表示x的父节点
用树(不一定是二叉树)的形式来维护集合:
集合的根结点为集合编号
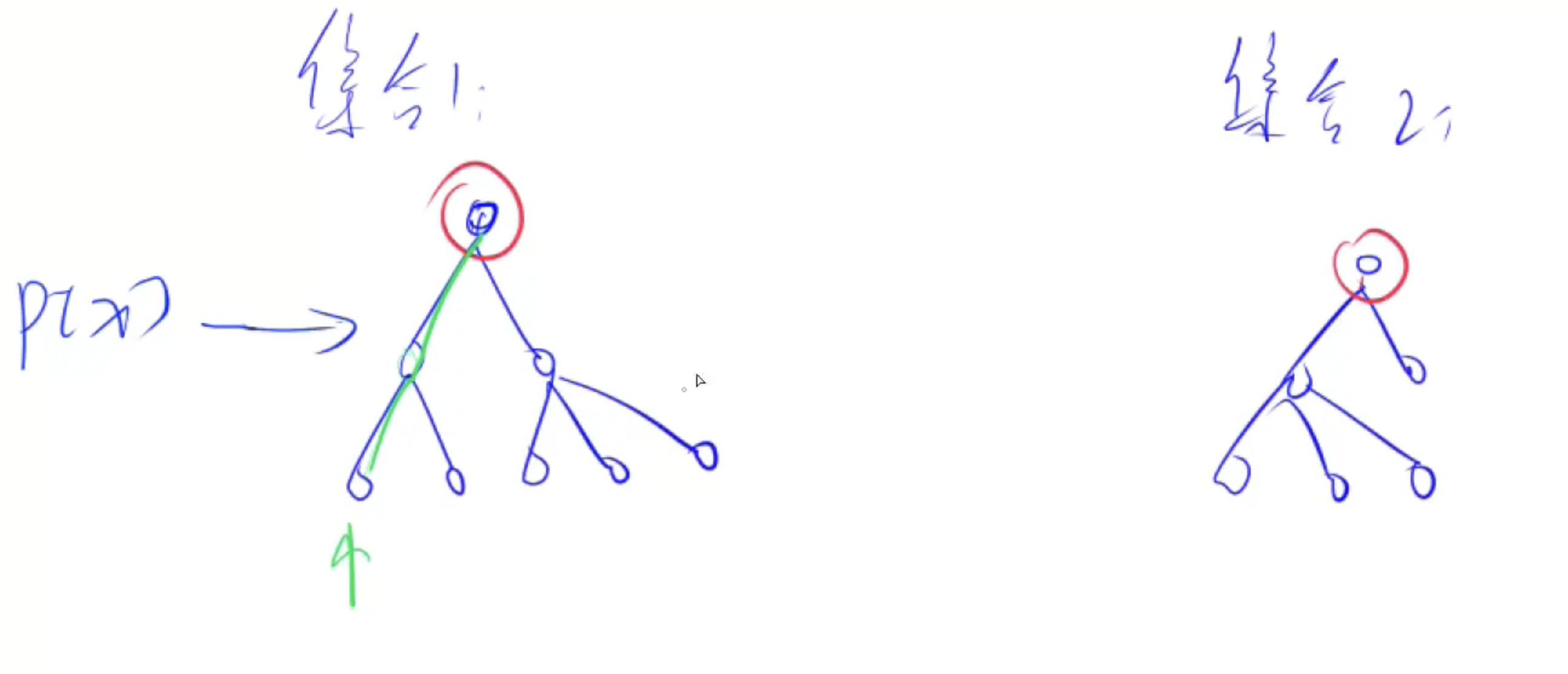
问题1:
- 如何判断树根:
if (p[x] == x) 根节点的parent是他自己
问题2:
- 如何求x的集合编号:
while (p[x] ≠ x) x = p[x]
问题3:
- 如何合并两个集合:
- 把其中一个集合当成另一个集合的儿子;
- p[x] = y (px 是 x的集合编号, py是y的集合编号)
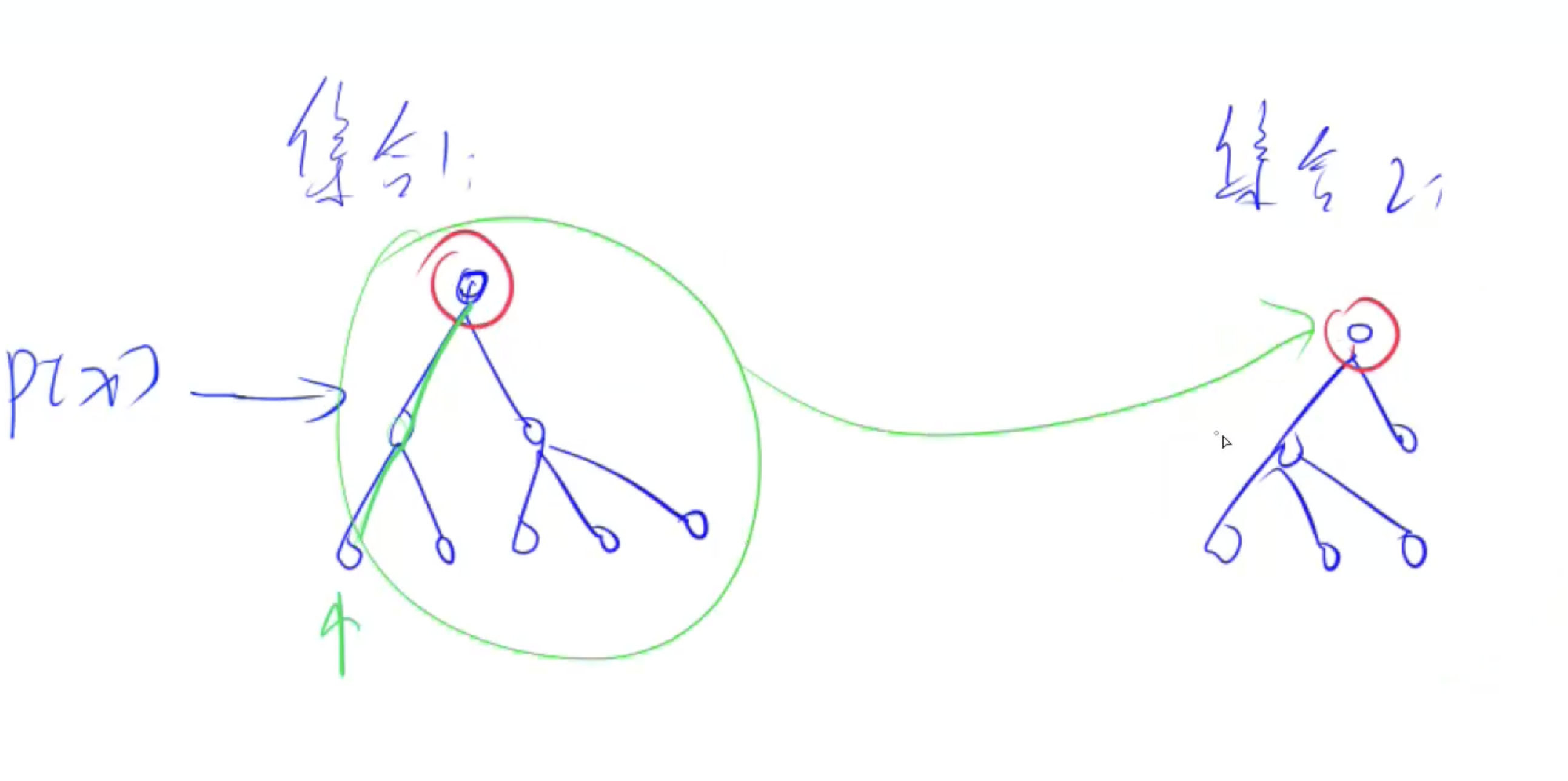
思考:插入需要树的高度的复杂度 → 并查集的优化:路经压缩
当第一次x节点后,当前路径上经过的所有点都直接指向根节点,因此近乎 O(1)
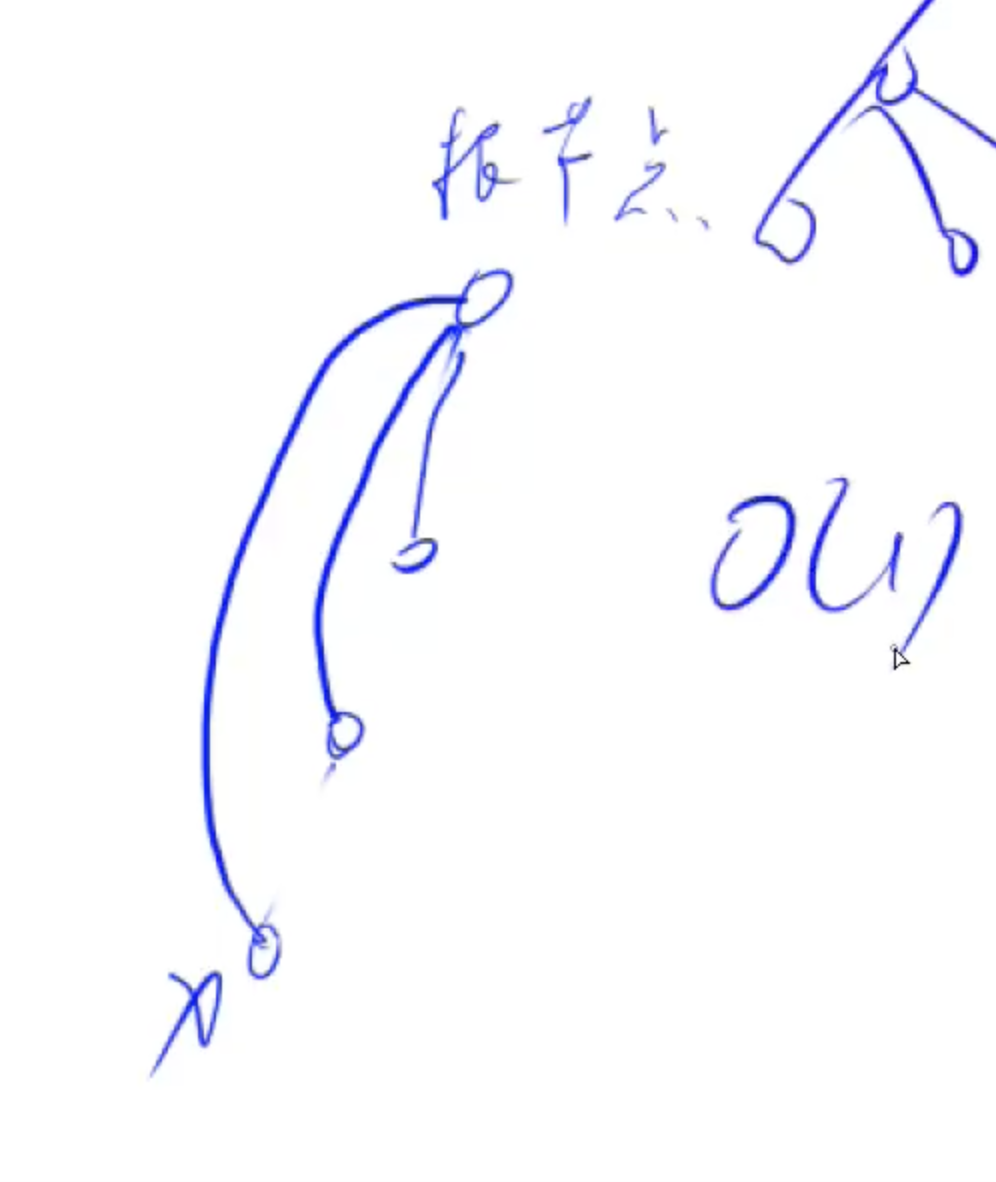
并且同时维护节点数量:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
| #include <iostream>
using namespace std;
const int N = 100010;
int n, m;
int p[N], cnt[N];
int find(int x)
{
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i ++ )
{
p[i] = i;
cnt[i] = 1;
}
while (m -- )
{
string op;
int a, b;
cin >> op;
if (op == "C")
{
cin >> a >> b;
a = find(a), b = find(b);
if (a != b)
{
p[a] = b;
cnt[b] += cnt[a];
}
}
else if (op == "Q1")
{
cin >> a >> b;
if (find(a) == find(b)) puts("Yes");
else puts("No");
}
else
{
cin >> a;
cout << cnt[find(a)] << endl;
}
}
return 0;
}
|
java 代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
| class UF {
private int count;
private int[] parent;
public UF(int n) {
this.count = n;
parent = new int[n];
for (int i = 0; i < n; i++) {
parent[i] = i;
}
}
public void union(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
if (rootP == rootQ)
return;
parent[rootQ] = rootP;
count--;
}
public boolean connected(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
return rootP == rootQ;
}
public int find(int x) {
if (parent[x] != x) {
parent[x] = find(parent[x]);
}
return parent[x];
}
public int count() {
return count;
}
}
|
这里的可以增加一个size数组,用来表示每一个联通块的大小
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| class UF {
int count;
int[] parent;
int[] size;
UF(int n) {
this.count = n;
this.parent = new int[n];
this.size = new int[n];
for (int i = 0; i < n; i++) {
parent[i] = i;
this.size[i] = 1;
}
}
void union(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
if (rootP == rootQ) return;
parent[rootQ] = rootP;
size[rootP] += size[rootQ];
count--;
}
int find(int cur) {
if (parent[cur] != cur) {
parent[cur] = find(parent[cur]);
}
return parent[cur];
}
}
|
函数方法
union很好理解,找到两个根,将其中一个根的parent设置成另一个根的儿子
主要是find,这里使用了路经压缩:
1
2
3
4
5
6
| public int find(int x) {
if (parent[x] != x) {
parent[x] = find(parent[x]);
}
return parent[x];
}
|
比如:
1
2
3
4
5
6
| 1 -> 2 2 -> 3 3 -> 3
4 -> 4
5 -> 6 6 -> 6
所以是 1->2->3; 4->4; 6->6; 三个集合
|
那么用 1->2->3举例子:1的父节点是2,2的父节点是3,而3是其自己的父节点。
如果我们调用find(1):
parent[1] 是 2,不等于1,所以我们要递归地找find(2)。parent[2] 是 3,不等于2,所以我们要递归地找find(3)。parent[3] 是 3,等于3,所以返回3。
在这个过程中,我们还会更新parent[1]和parent[2]都为3,因为3是1和2的代表。这就是路径压缩的优化,确保每个节点都直接指向其代表,从而使得后续的查找操作更快。
等于说:
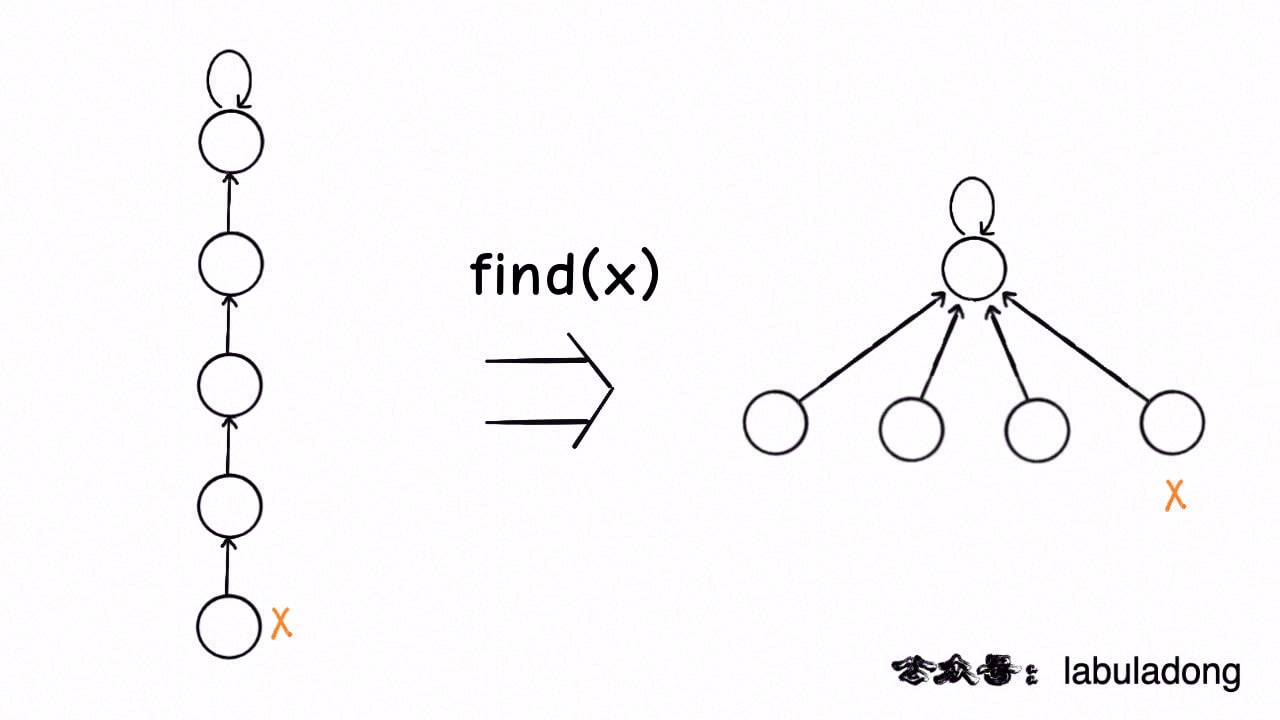
例题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
| class Solution {
int[] dx = new int[] {1, 0, 0, -1};
int[] dy = new int[] {0, 1, -1, 0};
class UnionFind {
private int count;
private int[] parent;
public UnionFind(char[][] grid) {
int n = grid.length;
int m = grid[0].length;
parent = new int[n * m];
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (grid[i][j] == '1') {
parent[i * m + j] = i * m + j;
count++;
}
}
}
}
public int find(int x) {
if (parent[x] != x) {
parent[x] = find(parent[x]);
}
return parent[x];
}
public void union(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
if (rootP == rootQ) return;
parent[rootQ] = rootP;
count--;
}
}
public int numIslands(char[][] grid) {
int n = grid.length;
int m = grid[0].length;
UnionFind uf = new UnionFind(grid);
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (grid[i][j] == '1') {
grid[i][j] = '0';
for (int dir = 0; dir < 4; dir++) {
int newX = i + dx[dir], newY = j + dy[dir];
if (newX >= 0 && newX < n && newY >= 0 && newY < m && grid[newX][newY] == '1') {
uf.union(
i * m + j, newX * m + newY
);
};
}
}
}
}
return uf.count;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
| class Solution {
class UnionFind {
int[] parent;
int count;
UnionFind(List<List<String>> accounts) {
int size = accounts.size();
parent = new int[size];
for (int i = 0; i < accounts.size(); i++) {
parent[i] = i;
}
}
public int find(int x) {
if (parent[x] != x) parent[x] = find(parent[x]);
return parent[x];
}
public void union(int p, int q) {
int rootQ = find(q);
int rootP = find(p);
if (rootQ == rootP) return;
parent[rootQ] = rootP;
count--;
}
}
public List<List<String>> accountsMerge(List<List<String>> accounts) {
UnionFind uf = new UnionFind(accounts);
Map<String, Integer> emailToId = new HashMap<>();
for (int i = 0; i < accounts.size(); i++) {
int num = accounts.get(i).size();
for (int j = 1; j < num; j++) {
String curEmail = accounts.get(i).get(j);
if (!emailToId.containsKey(curEmail)) {
emailToId.put(curEmail, i);
} else {
uf.union(i, emailToId.get(curEmail));
}
}
}
Map<Integer, List<String>> idToEmails = new HashMap<>();
for (Map.Entry<String, Integer> entry : emailToId.entrySet()) {
int id = uf.find(entry.getValue());
List<String> emails = idToEmails.getOrDefault(id, new ArrayList<>());
emails.add(entry.getKey());
idToEmails.put(id, emails);
}
List<List<String>> res = new ArrayList<>();
for(Map.Entry<Integer, List<String>> entry : idToEmails.entrySet()){
List<String> emails = entry.getValue();
Collections.sort(emails);
List<String> tmp = new ArrayList<>();
tmp.add(accounts.get(entry.getKey()).get(0));
tmp.addAll(emails);
res.add(tmp);
}
return res;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
| class Solution {
class UnionFind {
int[] parent;
int count;
UnionFind(int n) {
parent = new int[n];
count = n;
for (int i = 0; i < n; i++) {
parent[i] = i;
}
}
public void union(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
if (rootP == rootQ) return;
count--;
parent[rootQ] = rootP;
}
public int find(int x) {
if (parent[x] != x) {
parent[x] = find(parent[x]);
}
return parent[x];
}
public int getCount() {
return this.count;
}
}
public int countComponents(int n, int[][] edges) {
UnionFind uf = new UnionFind(n);
for (int i = 0; i < edges.length; i++) {
int p = edges[i][0], q = edges[i][1];
uf.union(p, q);
}
return uf.getCount();
}
}
|
并查集:
树满足两个性质:
- n 个节点 n - 1条边
- 无环
如果一个联通块下相连了两个节点,那么成环:
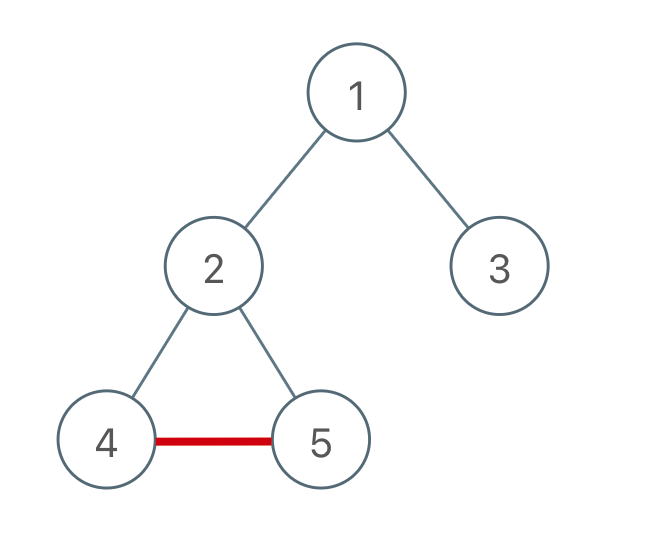
这种无环:
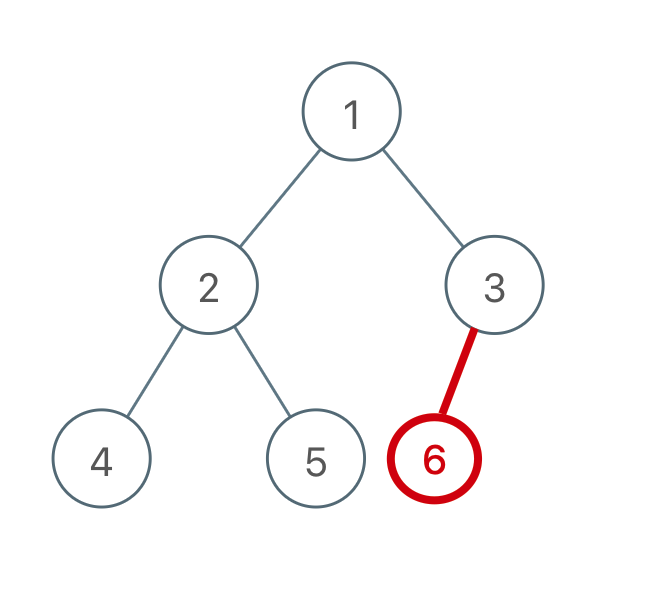
对于添加的这条边,如果该边的两个节点本来就在同一连通分量里,那么添加这条边会产生环;反之,如果该边的两个节点不在同一连通分量里,则添加这条边不会产生环。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
| class Solution {
class UnionFind {
int[] parent;
UnionFind(int n) {
parent = new int[n];
for (int i = 0; i < n; i++) {
parent[i] = i;
}
}
int find(int x) {
if (parent[x] != x) {
parent[x] = find(parent[x]);
}
return parent[x];
}
void union(int p, int q) {
int rootP = find(p), rootQ = find(q);
if (rootP == rootQ) return;
parent[rootQ] = rootP;
}
boolean isConnected(int p, int q) {
int rootP = find(p), rootQ = find(q);
return rootP == rootQ;
}
}
public boolean validTree(int n, int[][] edges) {
if (n - 1 != edges.length) return false;
UnionFind uf = new UnionFind(n);
for (int i = 0; i < edges.length; i++) {
int p = edges[i][0], q = edges[i][1];
if (!uf.isConnected(p, q)) {
uf.union(p, q);
} else {
return false;
}
}
return true;
}
}
|
DFS + Visited
比较困难的地方在于如何能够判断环即如何使用visited数组,由于这是个无向图,那么比如 0 <-> 1 节点0在遍历邻居1后,邻居1还会遍历它的邻居0,所以会被visited阻止,解决办法是传入一个parent变量,从而可以追踪目前的父节点。当当前节点的邻居和父节点为同一节点时跳过。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
| class Solution {
boolean[] visited;
List<List<Integer>> graph = new ArrayList<>();
public boolean validTree(int n, int[][] edges) {
if (n - 1 != edges.length) return false;
buildGraph(n);
visited = new boolean[n];
for (int i = 0; i < edges.length; i++) {
int a = edges[i][0], b = edges[i][1];
add(a, b);
add(b, a);
}
if (!dfs(0, -1)) return false;
for (boolean v : visited) {
if (!v) return false;
}
return true;
}
private void buildGraph(int n) {
for (int i = 0; i < n; i++) {
graph.add(new ArrayList<>());
}
}
private void add(int from, int to) {
graph.get(from).add(to);
}
private boolean dfs(int cur, int parent) {
if (visited[cur]) return false;
visited[cur] = true;
List<Integer> neighbours = graph.get(cur);
for (int neig : neighbours) {
if (neig == parent) continue;
if (!dfs(neig, cur)) return false;
}
return true;
}
}
|