背包问题
背包问题
背包问题包含以下这些: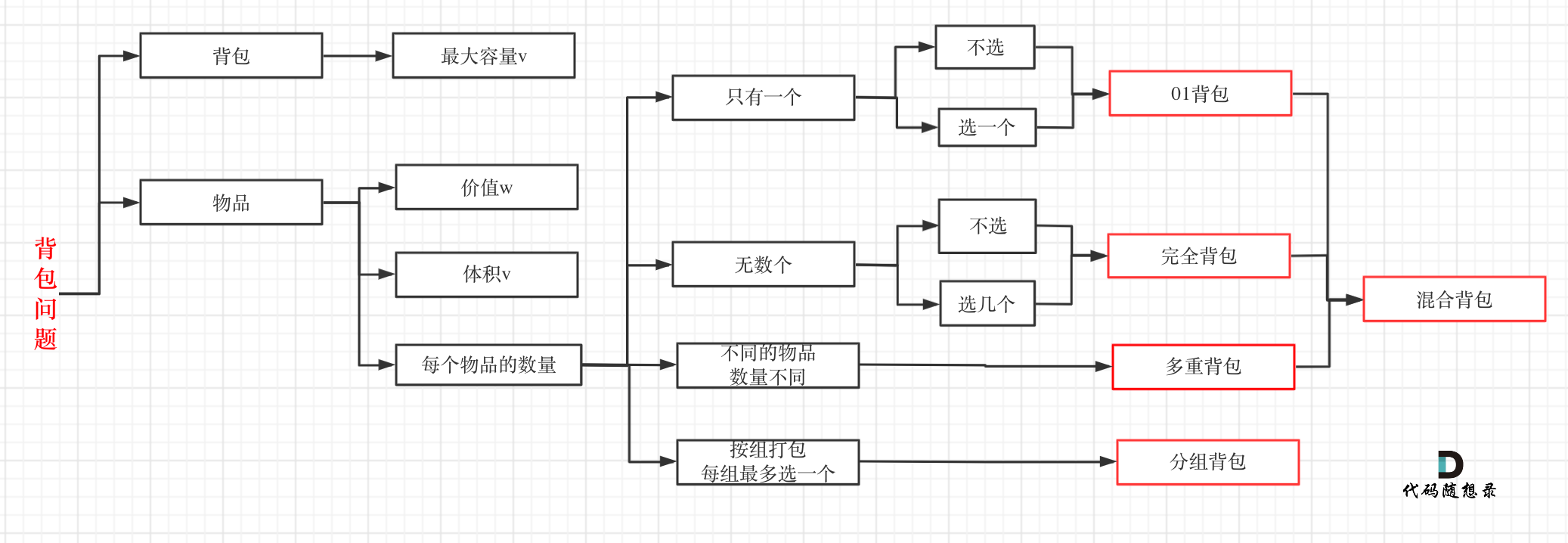
主要需要掌握的是01背包以及完全背包
完全背包是01背包的演化,完全背包的物品数量无限
01背包
定义:
有 n 件物品和一个最多能背重量为w的背包。
第 i件物品的重量是weight[i],可以得到的价值是value[i]。每件物品只能用一次
将哪些物品放入背包里物品价值总和最大。
暴力解法:对于每一个物品我们有两个选择,选或者不选,所以可以采用回溯法来搜索所有的情况时间复杂度为 O(2^n) n是物品数量
所以需要优化 穷举 + 求最值 -> 动态规划
题目假设
背包最大重量为4,有如下的物品:
| 重量 | 价值 | |
|---|---|---|
| 物品0 | 1 | 15 |
| 物品1 | 3 | 20 |
| 物品2 | 4 | 30 |
目前最大价值为 4 * 15 = 60
二维dp来解决01背包问题
分析dp数组含义
dp[i][j]用来表示从下标[0,i]的物品随便取一个,放进容量为j的背包,价值总和最大为多少递推公式
dp[i][j]能被转移过来的情况分成两种如果不放物品,就是从
dp[i - 1][j]转移而来,由于不放入新的重量所以其实重量就还是dp[i - 1][j]可能的场景是:当物品i的重量超过了背包能够承载的容积,新的物品i无法放入其中如果放物品,考虑
dp[i - 1][j - weight[i]]含义为背包容量为j - weight[i]时候的不放入i所能获得的最大价值,贪心一点,我们必须要腾出这部分的空间才行因为我们要保证背包是一直饱和的状态是当时的最优解。在0-1背包问题中,
dp[i][j]通常表示前i个物品填满背包容量为j的最大价值。dp[i - 1][j - weight[i]]表示的是在背包容量为j-weight[i]的时候,前i-1个物品的最大价值。之所以使用这个状态转移方程,是因为我们在考虑是否将第i个物品放入背包时,需要先确定在还没有放入第i个物品,并且背包容量为j-weight[i]时的最大价值。这里的“j - weight[i]”是为了腾出第i个物品所需的空间,以便我们能够将其放入背包。之后,我们将该物品的价值
value[i]加上dp[i - 1][j - weight[i]],这样就能得到在将第i个物品放入背包的情况下,能够得到的最大价值。简单来说,
dp[i - 1][j - weight[i]] + value[i]就表示:在考虑放入第i个物品(即在已经腾出了第i个物品所需的空间后),我们能够得到的最大价值。如果不把这个空间腾出来,那我们就没有地方放这个物品。初始化
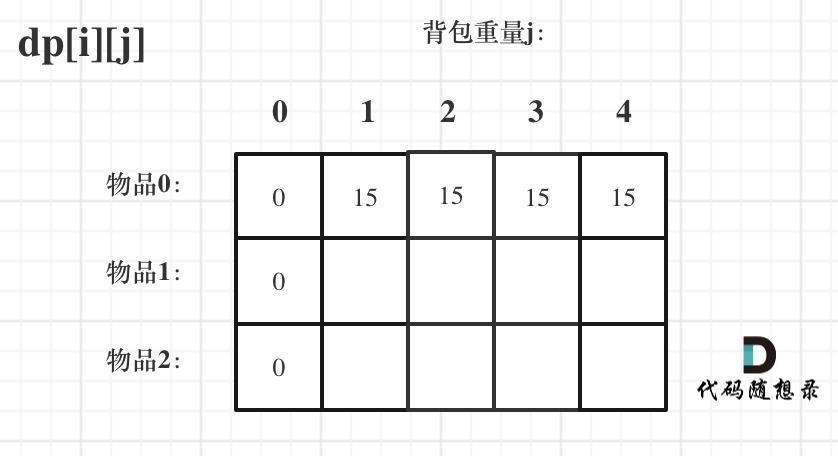
我们首先要对一个二维的数组来进行初始化因此需要搞清楚 [i] 和 [j] 的含义
回想定义:
dp[i][j]用来表示从下标[0,i]的物品随便取一个,放进容量为j的背包,价值总和最大为多少那么
dp[i][0]指的是如果背包容量j为0,表示从下标[0,i]的物品随便取一个,放进容量为0的背包,价值总和最大为多少,那么明显是0其次由于我们需要使用
dp[i - 1][j]来作为其中一项来推导dp[i][j]因此我们需要初始化dp[0][j]即,存放编号0的各种容量的背包中能获得的最大价值那么会有两种情况:当
j < weight[0]的时候,dp[0][j]应该是 0,因为背包容量比编号0的物品重量还小。当
j >= weight[0]时,dp[0][j]应该是value[0],因为背包容量放足够放编号0物品。
综上,对于上面的例子我们有:
对于其他的,由于都会被转化并且被覆盖新值,因此无论初始化成什么都可以
确定遍历顺序
我们需要遍历是应该从物品[i]还是背包容积[j]开始
由于
dp[i][j]所需要的数据就是左上角
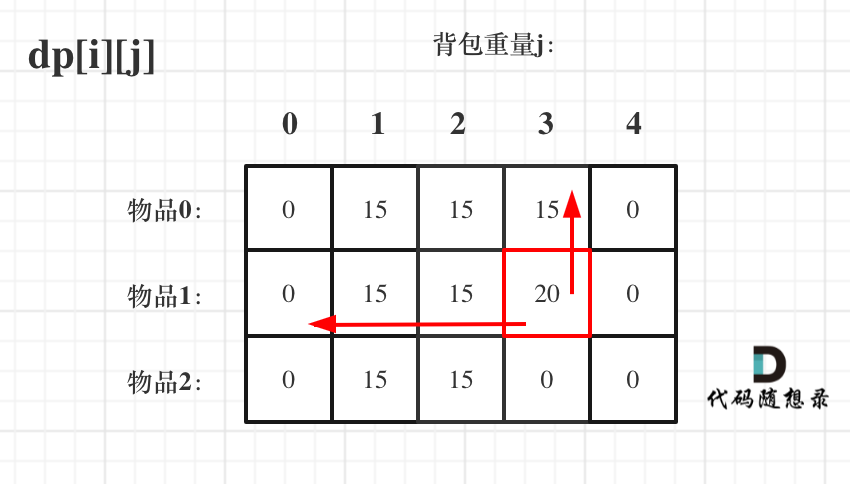
所以无论从哪里开始都可以得到结果
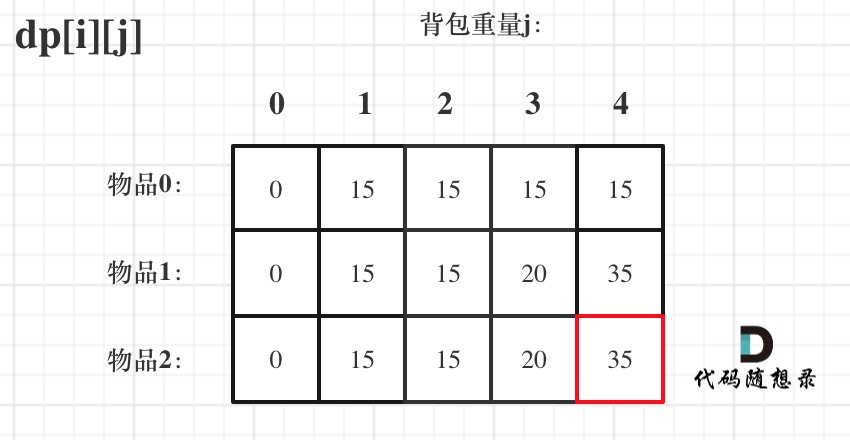
- 举例推导dp数组
滚动数组优化
由于dp[i][j]仅依赖于前一个物品的值(dp[i - 1][j] 和 dp[i - 1][j - weight[i]]),所以实际上我们并不需要维护一个二维数组,只需要一个一维数组就足够了。这个问题的特殊之处在于,dp[i][j]的值只依赖于dp[i-1][*],即只依赖于前一个物品的状态。这给我们提供了一个优化空间,那就是我们其实不需要存储所有的i,也就是不需要存储所有物品的状态,只需要存储前一个物品的状态就足够了。这就是为什么我们可以省去一个维度的原因。我们使用一维数组dp[j]来替代二维数组dp[i][j]。在每一次的迭代中,dp[j]表示的都是在考虑当前物品,并且在背包容量为j的情况下,我们能获得的最大价值。换句话说,我们的一维数组dp[j]在每次迭代过程中,都相当于原来二维数组的dp[i][j]。
- dp数组含义:
此时的含义就变为:
我们有容量为j的背包从前i个物品取能取到的最大价值
- 转移方程递推公式:
此时dp[j]有两个选择,一个是取自己dp[j] 相当于 二维dp数组中的dp[i-1][j],即不放物品i,一个是取dp[j - weight[i]] + value[i],即放物品i,指定是取最大的,毕竟是求最大价值,
即:
1 | dp[j] = max(dp[j], dp[j - weight[i]] + value[i]) |
- 初始化:
最初dp[0]容量为0的背包,那么最大价值一定为0
- 遍历顺序
重点:在这个优化策略中,我们必须从大到小遍历j,这是因为dp[j - weight[i]]必须在dp[j]之前更新。原因是我们在每次迭代中都在复用上一轮迭代中的结果。为了确保这次迭代的结果不会影响到下一次迭代,我们需要从大到小遍历j。
具体地说,如果我们从小到大遍历j,考虑在计算dp[j]时,由于dp[j - weight[i]]可能在这个迭代过程中已经被更新过(因为j - weight[i] < j),我们就会使用到这个物品i在多次的情况,这明显违反了我们的原始假设(每个物品只能用一次)。为了避免这个问题,我们选择从大到小遍历j,在计算dp[j]时,dp[j - weight[i]]对应的就是上一轮迭代的结果,也就是没有使用过物品i的情况。
例如,假设我们有物品的重量和价值分别为2和3,背包的容量为4,初始化dp数组为0。如果从小到大遍历j,计算过程如下:
- 当j=2时,dp[2] = max(dp[2], dp[2-2] + 3) = 3
- 当j=3时,dp[3] = max(dp[3], dp[3-2] + 3) = 3
- 当j=4时,dp[4] = max(dp[4], dp[4-2] + 3) = 6
在这个例子中,dp[4]的值为6,明显不对,因为我们的物品只有一个,但我们却计算得到了两个物品的价值,这就是因为在计算dp[4]时,dp[2]已经使用过当前物品,被更新为3了。
结论:从后往前循环,每次取得状态不会和之前取得状态重合,这样每种物品就只取一次了。
例题
416. 分割等和子集
第一个难点是如何转化为01背包问题:
这道题首先我们要等和,所以一个背包的容积就是 sum / 2
那么我们就是看是不是给一个可装载重量为 sum / 2 的背包和 N 个物品,每个物品的重量为 nums[i]。现在让你装物品,是否存在一种装法,能够恰好将背包装满?
注意不能直接看除2是否能除尽,因为除2不代表有对应的子集比如[1,2,5]
dp 数组的定义:dp[i][j] = x 表示,对于前 i 个物品,当前背包的容量为 j 时,若 x 为 true,则说明可以恰好将背包装满,若 x 为 false,则说明不能恰好将背包装满。
根据 dp 数组含义,可以根据「选择」对 dp[i][j] 得到以下状态转移:
如果不把 nums[i] 算入子集,或者说你不把这第 i 个物品装入背包,那么是否能够恰好装满背包,取决于上一个状态 dp[i-1][j],继承之前的结果。
如果把 nums[i] 算入子集,或者说你把这第 i 个物品装入了背包,那么是否能够恰好装满背包,取决于状态 dp[i-1][j-nums[i-1]]。
1 | class Solution { |
滚动数组优化:
相当于i直接就是每一层搞一次,但我们不用存储 i - 1的结果了,直接覆盖就可以了
Eg: [1,2,5]
| 0 | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| 0 | t | f | f | f | f |
| 1 | t | t | f | f | f |
| 2 | t | t | t | t | f |
| 3 | t | t | t | t | f |
1 | class Solution { |
1049.最后一块石头的重量 II
和416类似,重点是要知道如何转换为01背包问题
对于石头问题,我们想要的是尽量让两边相等然后看差值。
那么就是有个容量为 sum/2的背包,里面能够装的最大的重量,就是尽可能让两边相等的解法。
所以就是:
对于容积为sum/2的背包,我们有 stones[i] 价值的,重量为stones[i]的石头,怎么放,价值最大:
常规的二维dp:
注意labuladong和代码随想录不一样,labuladong的i从1开始然后 i - 1是对应的价值。而代码随想录从0开始,i就是对应的价值了
1 | class Solution { |
滚动数组优化,注意遍历顺序,(虽然道理已经明白了,可是还是不太懂这个到底是怎么优化的。。。)
1 | class Solution { |
494. 目标和
本题的关键难点在于如何做好问题转化,即怎么把这个问题转换为01背包问题:
这是一个经典的子集和问题(subset sum problem)转化。原始问题是从数组 nums 中选取若干数,可以加上+或-号,使得它们的总和为 target。问题被转化为找出 nums 中有多少个子集 A 使得这个子集的和等于 (target + sum(nums)) / 2。
为什么要这样转化呢?我们来详细理解下。
原始方程是:
[ sum(A) - sum(B) = target ]
其中,A 是被加上 + 号的子集,B 是被加上 - 号的子集。
再加上以下方程:
[ sum(A) + sum(B) = sum(nums) ]
两边都加上 sum(A):
[ 2 \times sum(A) = target + sum(nums) ]
从这个方程,我们得到:
[ sum(A) = (target + sum(nums)) / 2 ]
这就将原始问题转化为一个子集和问题,即从 nums 中找到所有子集 A,其和为 (target + sum(nums)) / 2。这是一个经典的动态规划问题,通常使用一个二维数组 dp 来解决。dp[i][j] 表示使用前 i 个数字,能否组成和为 j 的子集。
那么为什么是(target + sum(nums)) / 2 而不是 target呢?
假设nums: [1,2,3,4] 和 target:4 。
首先,我们看转化的方法:
从
nums中选择数字,有的加上+号,有的加上-号,使其总和为target。使用转化方法,我们得到以下方程:
[ sum(A) - sum(B) = target ]
[ sum(A) + sum(B) = sum(nums) ]
代入第一个方程得到:
[ sum(A) = (target + sum(nums)) / 2 ]
[ sum(A) = (4 + 10) / 2 = 7 ]
所以,我们需要找到 nums 中子集和为7的所有情况。
以下是子集和为7的组合:
- [1,2,4]
- [3,4]
这些组合可以得到如下的表示达到 target 4:
- +1+2+4-3
- +3+4-1-2
现在,如果我们直接找出 nums 中的子集和为 target=4 的组合,我们得到:
- [1,3]
- [4]
这些组合表示了如何通过简单组合 nums 中的数字得到4,但没有表示如何通过加法和减法操作得到4。这就是为什么直接使用 target 作为背包容量是不准确的,因为你只能得到部分答案,而不能表示如何通过整个 nums 数组的加减操作得到目标值 target。
1 | class Solution { |
二维变一维:
1 | class Solution { |




