Blind-Sheet

❓ -> 虽然做出了但有更妙的解法

Array

57. 插入区间 [❌]

这道题主要是两个考点

1. 分类讨论：

   设newInterval 为 [L,R]

   Intervals[i] 为 [cL, cR]

   完全不重叠的情况：

   cR < L 即 intervals[i] 在 [L,R]左方

   R < cL 即 intervals[i] 在 [L,R]右方

   那么其他的情况即为可能出现重叠的情况

2. 什么时候加入答案

   如果每次更新都加入答案就会重复加入，因此我们只需要在碰到不重叠的时候加入一次即可。

   由于按照左端点排序，因此第一个不重叠的位置就是R < cL

3. 最后对于空数组的处理我们可以用一个flag，如果更新过的答案之前加入过，那么就可以跳过。如果没有加入过说明是第一次加入，那么就加入答案数组，避免数组为空

class Solution {
    public int[][] insert(int[][] intervals, int[] newInterval) {
        int cur = 0;
        int length = intervals.length;
        List<int[]> res = new ArrayList<>();
        int newLeft = newInterval[0], newRight = newInterval[1];
        boolean insearted = false;
        for (; cur < length; cur++) {
            int curLeft = intervals[cur][0], curRight = intervals[cur][1];
            if (curLeft > newRight) {
                if (!insearted) {
                    res.add(new int[] {newLeft, newRight});
                    insearted = true;
                }
                res.add(new int[]{curLeft, curRight});
            } else if (curRight < newLeft) {
                res.add(new int[]{curLeft, curRight});
            } else {
                newLeft = Math.min(curLeft, newLeft);
                newRight = Math.max(curRight, newRight);
            }
        }

        if (!insearted) {
            res.add(new int[] {newLeft, newRight});
        }

        int[][] ret = new int[res.size()][2];
        for (int i = 0; i < res.size(); i++) {
            ret[i] = res.get(i);
        }
        return ret;
    }
}

15. 三数之和 [✅]

相向双指针应用题

本题主要考察两个：

1. 循环不变量
2. 两数之和的相向双指针

（其实挺简单的就是不要迷）

固定左边，那么中间的和右边的指针就是两数之和问题，然后为了解决重复的数组问题，那么需要在检查到和之前数相同时直接跳过就好了：

class Solution {
    public List<List<Integer>> threeSum(int[] nums) {
        Arrays.sort(nums);
        // Arrays.stream(nums).forEach(a -> System.out.print(a + " "));
        // System.out.println();
        int n = nums.length;
        int i = 0;
        List<List<Integer>> ret = new ArrayList<>();
        for (;i < n - 2; ) {
            if (i != 0 && nums[i] == nums[i - 1]) {
                i++;
                continue;
            }
            int j = i + 1;
            int k = n - 1;
            while (j < k) {
                // System.out.println(nums[i] + " " + nums[j] + " " + nums[k]);
                if (j != i + 1 && nums[j] == nums[j - 1]) {
                    j++;
                    continue;
                }
                if (nums[i] + nums[j] + nums[k] < 0) {
                    j++;
                } else {
                    if (k != n - 1 && nums[k] == nums[k + 1]) {
                        k--;
                        continue;
                    }
                    if (nums[i] + nums[j] + nums[k] == 0) {
                        List<Integer> list = new ArrayList<Integer>();
                        list.add(nums[i]);
                        list.add(nums[j]);
                        list.add(nums[k]);
                        ret.add(list);
                    }
                    k--;
                }
            }
            i++;
        }
        return ret;
    }
}

238. 除自身以外数组的乘积 [✅]

前缀和思想： 额外空间 O(N) 做法：

class Solution {
    public int[] productExceptSelf(int[] nums) {
        int n = nums.length;
        int[] prefixMulti = new int[n];
        int[] suffixMulti = new int[n];
        for (int i = 0; i < nums.length; i++) {
            if (i == 0) {
                prefixMulti[i] = 1;
                suffixMulti[n - i - 1] = 1;
                continue;
            }
            prefixMulti[i] = nums[i - 1] * prefixMulti[i - 1];
            suffixMulti[n - i - 1] = nums[n - i] * suffixMulti[n - i];
        }
        // Arrays.stream(prefixMulti).forEach(a -> System.out.print(a + " "));
        // System.out.println();
        // Arrays.stream(suffixMulti).forEach(a -> System.out.print(a + " "));
        // System.out.println();

        int[] res = new int[n];
        for (int i = 0; i < n; i++) {
            res[i] = prefixMulti[i] * suffixMulti[i];
        }
        return res;
    }
}

为了省去额外的空间，我们可以采取使用res数组作为中间的用于计算前缀积

class Solution {
    public int[] productExceptSelf(int[] nums) {
        int n = nums.length;
        int[] res = new int[n];
        res[0] = 1;
        for (int i = 1; i < n; i++) {
            res[i] = res[i - 1] * nums[i - 1];
        }

        int suffixCur = 1;
        for (int i = n - 1; i >= 0; i--) {
            res[i] *= suffixCur;
            suffixCur *= nums[i];
        }

        return res;
    }
}

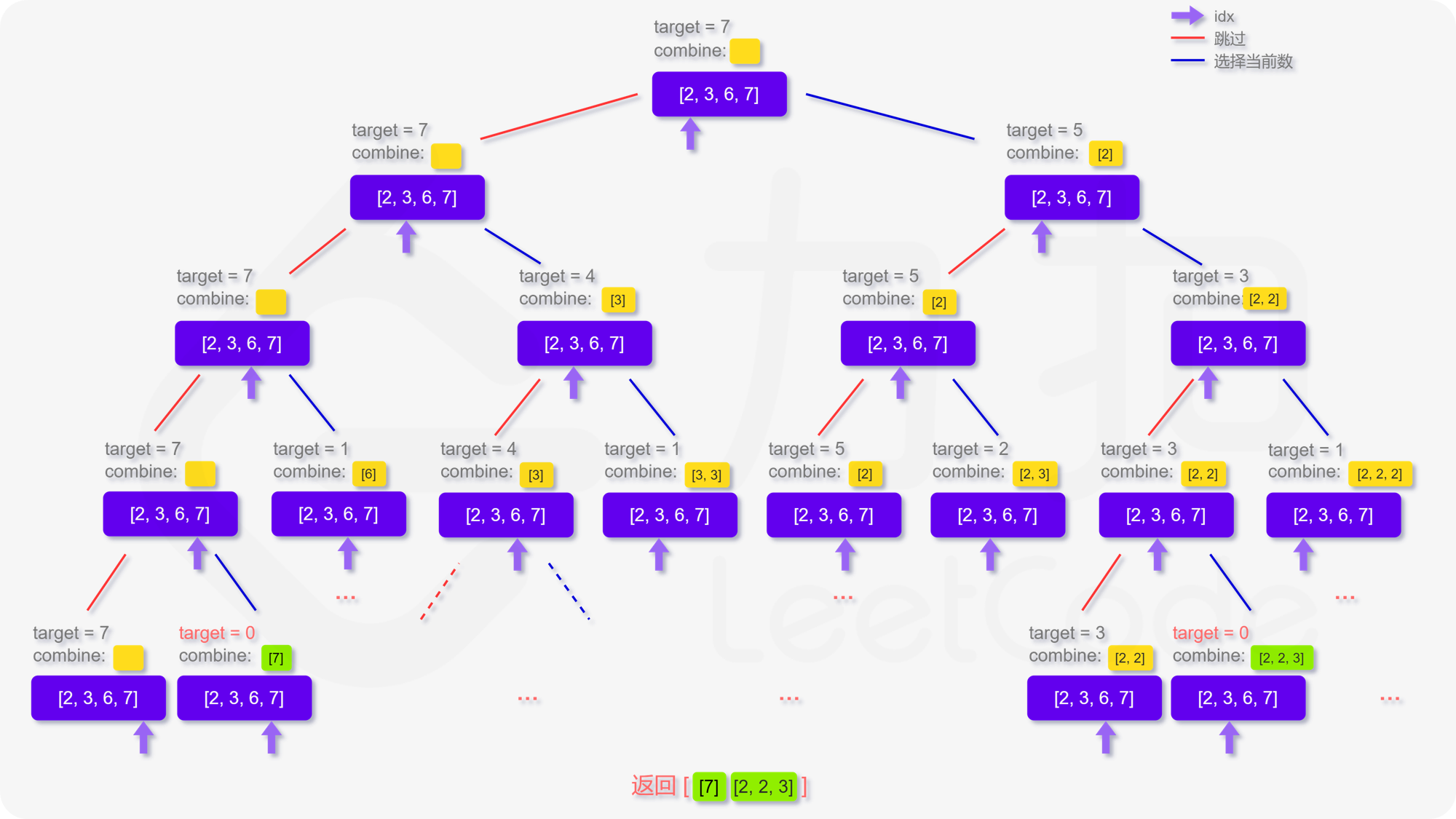
39. 组合总和 [✅]

回溯题，这是一个选或不选的问题：

class Solution {
    List<List<Integer>> res = new ArrayList<>();
    LinkedList<Integer> selected = new LinkedList<>();
    int[] candidates;
    int n;
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        // 暴搜
        this.candidates = candidates;
        n = candidates.length;
        dfs(0, target);
        return res;
    }
    private void dfs(int curIdx, int target) {
        if (curIdx == n || target < 0) return;
        if (target == 0) {
            res.add(new ArrayList<>(selected));
            return;
        }
        for (int i = curIdx; i < n; i++) {
            selected.addLast(candidates[i]);
            dfs(i, target - candidates[i]);
            selected.removeLast();
        }
    }
}

56. 合并区间 [✅]

和插入区间异曲同工，需要注意边界的处理

自己的方法：

对左端点排序，「延迟」（即到下一个不可以合并的区间时候）加入

class Solution {
    public int[][] merge(int[][] intervals) {
        Arrays.sort(intervals, new Comparator<>(){
            @Override
            public int compare(int[] a, int[] b) {
                return a[0] - b[0];
            }
        });
        List<int[]> ls = new ArrayList<>();
        int n = intervals.length;
        int pStart = intervals[0][0], pEnd = intervals[0][1];
        if (n == 1) {
            return new int[][]{{pStart, pEnd}};
        }
        for (int i = 1; i < n; i++) {
            int[] interval = intervals[i];
            int start = interval[0], end = interval[1];
            // System.out.println(pStart + " " + pEnd + "; " + start + " " + end);
            if (pEnd >= start) {
                pStart = Math.min(pStart, start);
                pEnd = Math.max(pEnd, end);
            } else {
                ls.add(new int[]{pStart, pEnd});
                pStart = start;
                pEnd = end;
            }
        }
        ls.add(new int[]{pStart, pEnd});
        int[][] ret = new int[ls.size()][2];
        for (int i = 0; i < ls.size(); i++) {
            ret[i] = ls.get(i);
        }
        return ret;
    }
}

方法2:

用一个list merged 来表示已经处理好的部分，如果碰到不重叠的区间或者merged为空时，直接加入merged即可，其他时候可以查看merged的右端点并且不断更新其右端点

这个方法更好地利用了排序的性质

class Solution {
    public int[][] merge(int[][] intervals) {
        Arrays.sort(intervals, new Comparator<>(){
            @Override
            public int compare(int[] a, int[] b) {
                return a[0] - b[0];
            }
        });
        List<int[]> merged = new ArrayList<>();
        int n = intervals.length;

        for (int i = 0; i < n; i++) {
            int size = merged.size();
            if (size == 0 || merged.get(size - 1)[1] < intervals[i][0]) {
                merged.add(new int[]{intervals[i][0], intervals[i][1]});
            } else {
                merged.get(size - 1)[1] = Math.max(merged.get(size - 1)[1], intervals[i][1]);
            }
        }
        
        int[][] ret = new int[merged.size()][2];
        for (int i = 0; i < merged.size(); i++) {
            ret[i] = merged.get(i);
        }
        return ret;
    }
}

75. 颜色分类[❓]

这是一个考察循环不变量以及荷兰国旗的经典问题

1. 循环不变：

Bilibili - 循环不变量

2. 荷兰国旗

荷兰国旗的本质是要我们将数分成三段。

因此除了使用一个变量 cur 代指处理到哪一个 nums[cur] 以外，至少还需要两个变量来代指三段的边界：

• 变量 l 为下一个填入 0 的位置（因此范围 [0,l−1] 均为 0，初始化 l=0，代表空集）
• 变量 r 为下一个填入 2 的位置（因此范围 [r+1,n−1] 均为 2，初始化 r=n−1，代表空集)
• 由于 [0,cur−1] 均为处理过的数值（即 0 和 2 必然都被分到了两端），同时 l−1 又是 0 的右边界，因此 [l,cur−1] 为 1 的区间，而 [cur,r] 为未处理的数值。

分情况讨论：

1. nums[cur]=0：此时将其与位置 l 进行互换（ l 为下一个待填入 0 的位置，同时 [l,cur−1] 为 1 的区间），本质是将nums[cur] 的 0 和 nums[l] 的 1 进行互换，因此互换后将 l 和 cur 进行右移；
2. nums[cur]=1：由于[l,cur−1] 本身就是 1 的区间，直接将 cur 进行右移即可；
3. nums[cur]=2：此时将其与位置 r 进行互换（r 为下一个待填入 2 的位置，但 [cur,r] 为未处理区间），也就是我们互换后，只能明确换到位置 nums[r] 的位置为 2，可以对 r 进行左移，但不确定新 nums[cur] 为何值，因此保持 cur 不变再入循环判断。
4. 最后当 cur>r（含义为未处理区间为空集），整个分三段过程结束。

class Solution {
    public void sortColors(int[] nums) {
        int n = nums.length;
        int l = 0, r = n - 1;
        // [0, l - 1] 0
        // [0, cur - 1] 已经处理完
        // [l, cur - 1] 1
        // [cur, r] 待处理
        // [r + 1, n - 1] 2
        for (int cur = 0; cur <= r;) {
            System.out.println(l + " " + cur + " " + r);
            if (nums[cur] == 0) {
                swap(nums, l, cur);
                l++;
                cur++;
            } else if (nums[cur] == 1) {
                cur++;
            } else {
                swap(nums, cur, r);
                r--;
            }
        }
    }

    private void swap(int[] nums, int i, int j) {
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }
}

11. 盛最多水的容器

双指针应用题：

• 主要证明一点，我们应该固定长板，每一次都移动短板，因为只有移动短板才有可能会有更大的面积，而这是因为每一次收紧左右端点时候其都会变小。

class Solution {
    public int maxArea(int[] height) {
        int n = height.length;
        int l = 0, r = n - 1;
        int result = Integer.MIN_VALUE;
        while (l < r) {
            int curArea = calculateArea(l, r, height[l], height[r]);
            result = Math.max(curArea, result);
            if (height[l] < height[r]) l++;
            else r--;
        }
        return result;
    }

    private int calculateArea(int i, int j, int hi, int hj) {
        return Math.min(hi, hj) * (j - i);
    }
}

Stack

20. 有效的括号[✅]

栈就是括号问题的代名词

class Solution {
    public boolean isValid(String s) {
        Deque<Character> dq = new ArrayDeque<>();
        char[] sChar = s.toCharArray();
        int n = s.length();
        for (int i = 0; i < n; i++) {
            if (sChar[i] == '(' || sChar[i] == '{' || sChar[i] == '[') {
                dq.addLast(sChar[i]);
            } else {
                if (dq.isEmpty()) return false;
                char curLast = dq.peekLast();
                if (sChar[i] == ')') {
                    if (curLast != '(') return false;
                    else dq.pollLast();
                } else if (sChar[i] == ']') {
                    if (curLast != '[') return false;
                    else dq.pollLast();
                } else if (sChar[i] == '}') {
                    if (curLast != '{') return false;
                    else dq.pollLast();
                }
            }
        }
        return dq.isEmpty();
    }
}

42. 接雨水

三种解法：

第一类：纵向和

这种方法是在 i 上进行计算，即算当前的高，一列一列的加

前后缀分解 ：

前后缀分解比较好理解，有两个备忘录一个记录

height[0, i] 的最大值 lMax

height[i, n - 1] 的最大值 rMax

那么当前 i 的雨水就是 min(lMax, rMax) - height[i]

优化后的相向双指针：

但是可以省略这两个备忘录即使用相向双指针

但是这里不同的是

height[0, left] 的最大值 lMax

height[right, n - 1] 的最大值 rMax

不再是当前i而是left 和 right， 那么为什么可以保证这样是对的呢，这是因为当前i能接的雨水只看两遍的短的一边然后减去高度，也就是说重要的是 height[i] 能够装的水只和**Math.min(lMax, rMax)**相关（差）

第二类：横向和

这种方法类似于横向填充水泥。一行一行的加

单调栈

单调栈已经尝试多次

总结一下：

在需要更新栈中内容时，我们pop掉所有不符合要求的直至新加入的元素符合要求从而满足栈内元素单调。

class Solution {
    int[] height;
    public int trap(int[] height) {
        this.height = height;
        return twoPointers();
    }

    private int twoPointers() {
        int n = height.length;
        int left = 0, right = n - 1;
        int lMax = 0, rMax = 0;
        int tot = 0;
        while (left < right) {
            lMax = Math.max(lMax, height[left]);
            rMax = Math.max(rMax, height[right]);
            if (lMax < rMax) {
                tot += lMax - height[left];
                left++;
            } else {
                tot += rMax - height[right];
                right--;
            }
        }
        return tot;
    }

    private int monoStack() {
        Deque<Integer> stk = new ArrayDeque<>();
        int n = height.length;
        int tot = 0;
        for (int i = 0; i < n; i++) {
            while (!stk.isEmpty() && height[stk.peek()] <= height[i]) {
                int bottomColIdx = stk.pop();
                if (stk.isEmpty()) break;
                int left = stk.peek();
                int width = i - left - 1;
                int minHeight = Math.min(height[left], height[i]) - height[bottomColIdx];
                tot += width * minHeight;
            }
            stk.push(i);
        }
        return tot;
    }

    private int detachPrefixSuffix() {
        int n = height.length;
        int[] prefix = new int[n];
        prefix[0] = height[0];
        for (int i = 1; i < n; i++) {
            prefix[i] = Math.max(prefix[i - 1], height[i]);
        }

        int[] suffix = new int[n];
        suffix[n - 1] = height[n - 1];
        for (int i = n - 2; i >= 0; i--) {
            suffix[i] = Math.max(suffix[i + 1], height[i]);
        }

        int tot = 0;
        for (int i = 0; i < n; i++) {
            tot += calculateTrappedWater(prefix, suffix, i);
        }
        return tot;
    }

    private int calculateTrappedWater(int[] prefix, int[] suffix, int i) {
        return Math.min(prefix[i], suffix[i]) - this.height[i];
    }
}

Binary Tree

236. 二叉树的最近公共祖先

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        return dfs(root, p, q);
    }

    private TreeNode dfs(TreeNode cur, TreeNode p, TreeNode q) {
        if (cur == null) return null;
        if (cur == p || cur == q) return cur;
        TreeNode left = dfs(cur.left, p, q);
        TreeNode right = dfs(cur.right, p, q);
        if (left == null && right == null) {
            return null;
        } 
        if (left != null && right != null) return cur; // 在左右树上分别找到p和q，返回当前节点
        if (left == null) return right; // 左边没找到，说明全在右边，首先找到的p或q就是LCA
        else return left; // 右边没找到，说明全在左边，首先找到的p或q就是LCA
    }
}

102. 二叉树的层序遍历

简单的BFS

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        if (root == null) return new ArrayList<>();
        Deque<TreeNode> dq = new LinkedList<>();
        dq.addLast(root);
        List<List<Integer>> res = new ArrayList<>();
        while (!dq.isEmpty()) {
            List<Integer> level = new ArrayList<>();
            int size = dq.size();
            while (size > 0) {
                TreeNode cur = dq.pollFirst();
                level.add(cur.val);
                if (cur.left != null) {
                    dq.addLast(cur.left);
                }
                if (cur.right != null) {
                    dq.addLast(cur.right);
                }
                size--;
            }
            res.add(level);
        }
        return res;
    }
}

199. 二叉树的右视图

BFS很简单每一层最右边的加入

DFS就是先右子树，后左子树。然后有一个track来看这一层最右边的被加进来过没有。如果有之后就都不加了。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    LinkedList<Integer> res = new LinkedList<>();
    public List<Integer> rightSideView(TreeNode root) {
        dfs(root, 0);
        return res;
    }

    private void dfs(TreeNode root, int depthTrack) {
        if (root == null) return;
        
        if (depthTrack == res.size()) {
            res.add(root.val);
        }

        dfs(root.right, depthTrack + 1);
        dfs(root.left, depthTrack + 1);
    }
}

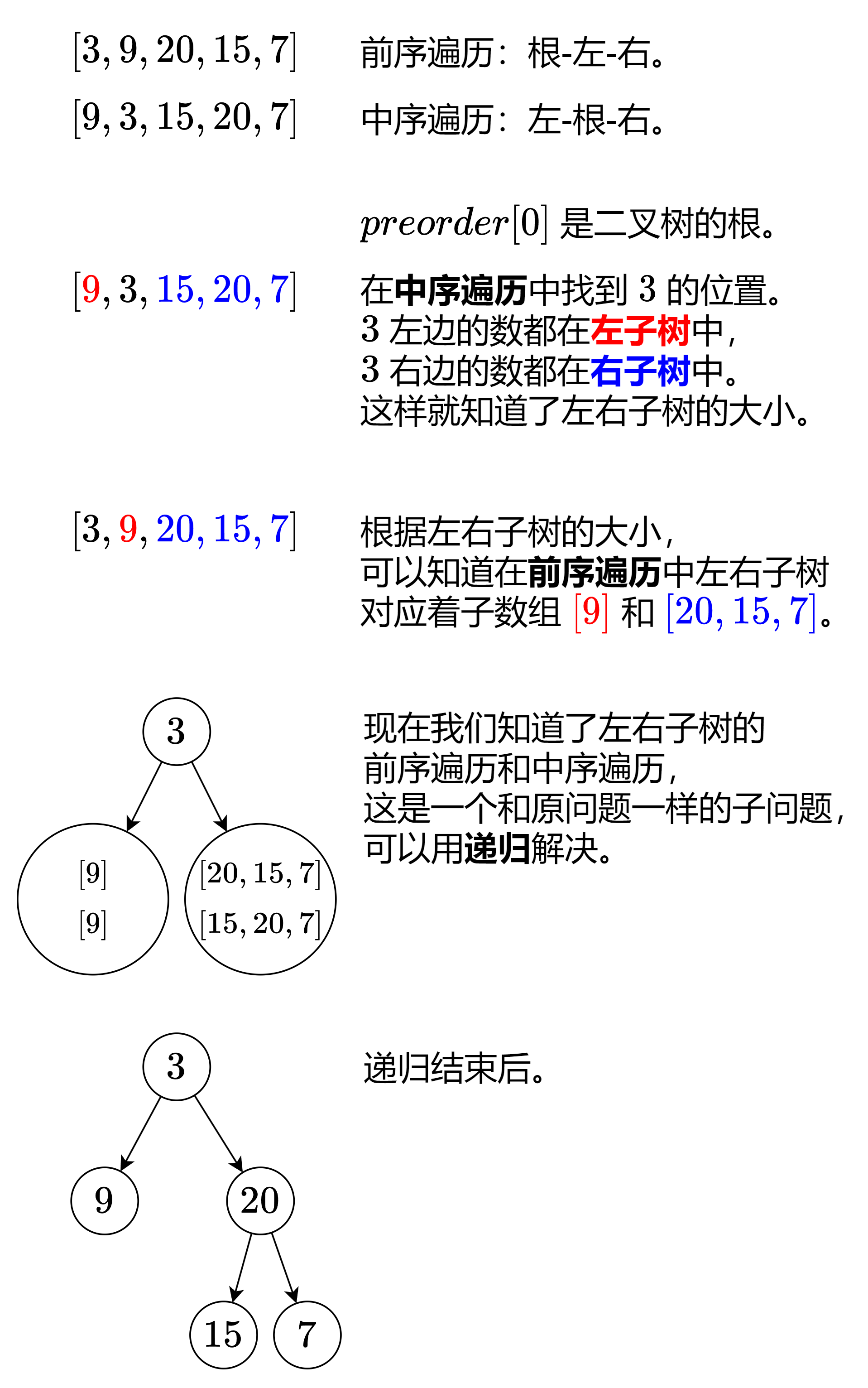
105. 从前序与中序遍历序列构造二叉树

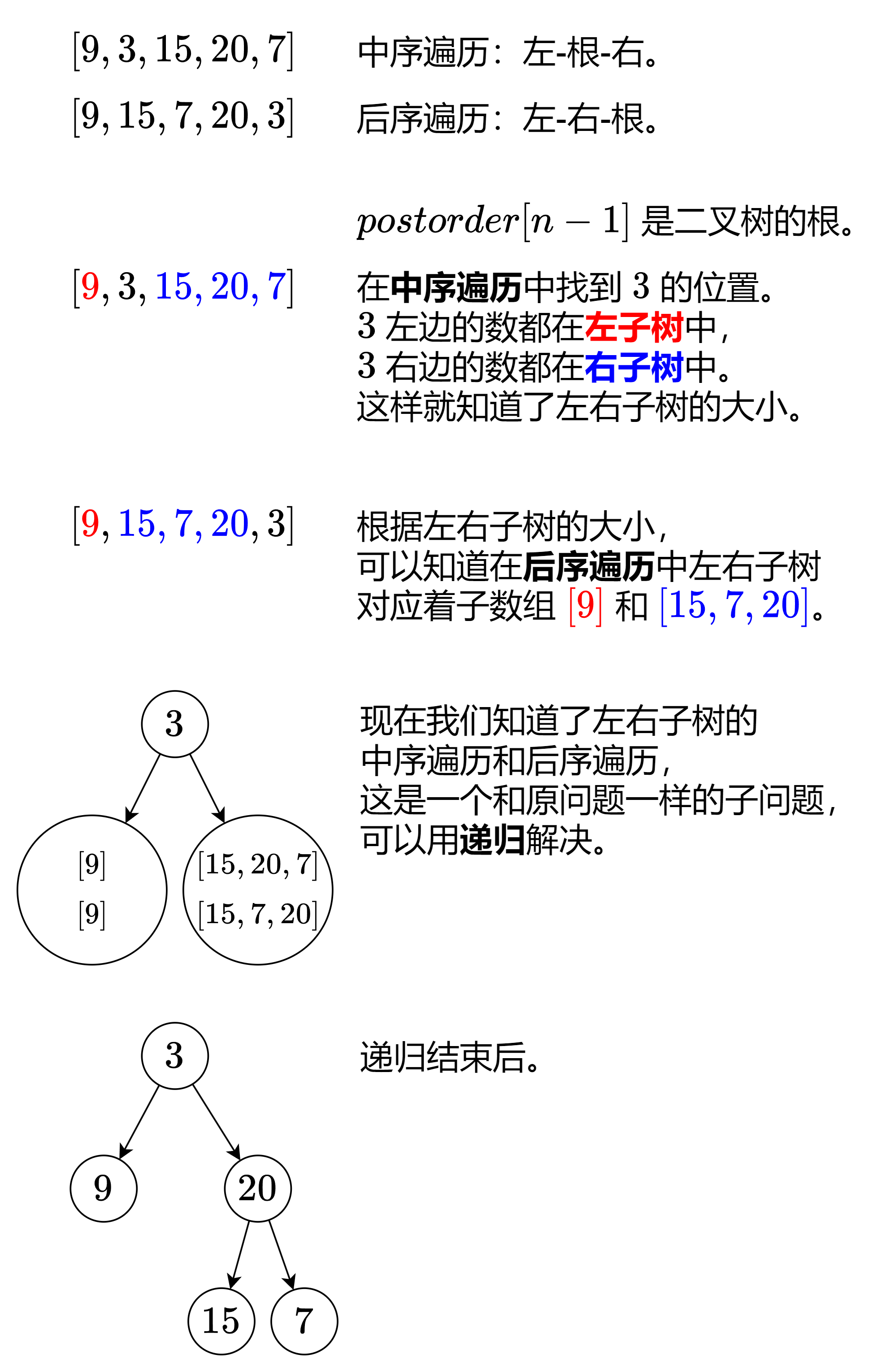
106. 从中序与后序遍历序列构造二叉树

这两题均属于构造类题目，具体可以看：
二叉树之构造类问题 中包含构造类问题的习题以及思路

核心思想都是通过构造左子树 + 右子树 连接根节点，只不过「细节和边界」略有不同，在尝试过后，使用左闭右开区间会稍微好处理一些

其实核心就是 子树 也是 树，所以递归的处理问题只要把大问题处理好小问题就可以很简单的处理了

105: 前序按照 中左右的顺序，所以可以先碰到的作为root节点然后递归的构造左右子树：

灵神 - 105

106: 后序按照 左右中的顺序，所以可以从右开始碰到的作为root节点然后递归的构造左右子树：

但是注意这里的区间略有不同

代码：

// 105:
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    int[] preorder;
    int[] inorder;
    Map<Integer, Integer> num2Idx = new HashMap<>();
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        // preorder 中左右 inorder 左中右
        // 恢复顺序 根，左右
        this.preorder = preorder;
        this.inorder = inorder;
        for (int i = 0; i < inorder.length; i++) {
            num2Idx.put(inorder[i], i);
        }

        TreeNode root = building(0, preorder.length - 1, 0, inorder.length - 1);
        return root;
    }

    private TreeNode building(int preStart, int preEnd, int inStart, int inEnd) {
        // System.out.println(preStart + " " + preEnd + " " + inStart + " " + inEnd);
        if (preStart > preEnd) return null;
        if (inStart > inEnd) return null;

        TreeNode root = new TreeNode(preorder[preStart]);
        int idxInorder = findNodeThruInorder(preorder[preStart]);
        int leftSize = idxInorder - inStart;

        // 递归构造左子树
        root.left = building(preStart + 1, preStart + leftSize, inStart, idxInorder);

        // 递归构造右子树
        root.right = building(preStart + leftSize + 1, preEnd, idxInorder + 1, inEnd);

        return root;
    }

    private int findNodeThruInorder(int val) {
        return num2Idx.get(val);
    }
}

// 106:
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    int[] inorder, postorder;
    Map<Integer, Integer> num2Idx = new HashMap<>();
    public TreeNode buildTree(int[] inorder, int[] postorder) {
        // 继续根左子树，右子树来构造
        // inorder 是 左中右， postorder 左右中
        // 后序遍历就是从根节点右往左而已
        this.inorder = inorder;
        this.postorder = postorder;
        for (int i = 0; i < inorder.length; i++) {
            num2Idx.put(inorder[i], i);
        }

        TreeNode root = building(0, inorder.length, 0, postorder.length);
        return root;
    }

    private TreeNode building(int postStart, int postEnd, int inStart, int inEnd) {
        // System.out.println(postStart + " " + postEnd + " " + inStart + " " + inEnd);
        if (postStart >= postEnd || inStart >= inEnd) return null;

        int val = postorder[postEnd - 1];
        TreeNode root = new TreeNode(val);
        int idx = num2Idx.get(val);
        int leftSize = idx - inStart;

        root.left = building(postStart, postStart + leftSize, inStart, idx);

        root.right = building(postStart + leftSize, postEnd - 1, idx + 1, inEnd);

        return root;
    }
}

297. 二叉树的序列化与反序列化

LC解法

两种解法一个DFS，一个BFS

DFS中还是延续了构造类问题的解法，构造 根 + 左子树 + 右子树

序列化：这里选择使用前序遍历，因为方便找到根节点当节点 = null时加入string

反序列化：dfs遍历，每一次移动一个位置，碰到 “null” 时return null，要不就构造节点

BFS是层序遍历，另外我们需要一个deque来保存制作好的节点在反序列化时移动left， rightcursor

// DFS
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
public class Codec {
    StringBuilder sb;
    String preOrder;
    // Encodes a tree to a single string.
    public String serialize(TreeNode root) {
        sb = new StringBuilder();
        buildWithPreOrder(root);
        preOrder = sb.toString();
        return preOrder;
    }

    private void buildWithPreOrder(TreeNode root) {
        if (root == null) {
            sb.append("null,");
            return;
        }

        sb.append(root.val + ",");
        buildWithPreOrder(root.left);
        buildWithPreOrder(root.right);
    }

    // Decodes your encoded data to tree.
    int idx = -1;
    public TreeNode deserialize(String data) {
        String[] dataLs = data.split(",");
        // Arrays.stream(dataLs).forEach(a -> System.out.print(a + " "));
        TreeNode root = building(dataLs);
        return root;
    }

    private TreeNode building(String[] dataLs) {
        idx++;
        if (idx >= dataLs.length) return null;
        if (dataLs[idx].equals("null")) {
            return null;
        }


        int val = Integer.valueOf(dataLs[idx]);
        TreeNode root = new TreeNode(val);
        root.left = building(dataLs);
        root.right = building(dataLs);

        return root;
    }
}

// BFS
public class Codec {

    // Encodes a tree to a single string.
    public String serialize(TreeNode root) {
        return bfsSerilize(root);
    }

    private String bfsSerilize(TreeNode root) {
        if (root == null) return "";
        Deque<TreeNode> dq = new LinkedList<>();
        dq.add(root);
        StringBuilder sb = new StringBuilder();
        while (!dq.isEmpty()) {
            int size = dq.size();
            TreeNode cur = dq.pollFirst();
            if (cur == null) {
                sb.append("null,");
            } else {
                sb.append(cur.val + ",");
                dq.addLast(cur.left);
                dq.addLast(cur.right);
            }
        }
        // System.out.println(sb.toString());
        return sb.toString();
    }

    // Decodes your encoded data to tree.
    public TreeNode deserialize(String data) {
        if (data.length() == 0) return null;
        String[] dataArr = data.split(",");
        Deque<TreeNode> dq = new LinkedList<>();
        TreeNode root = new TreeNode(Integer.valueOf(dataArr[0]));
        dq.addLast(root);
        int left = 1, right = left + 1;
        while (left < dataArr.length && right < dataArr.length) {
            String curLeft = dataArr[left], curRight = dataArr[right];
            TreeNode cur = dq.pollFirst();
            if (!curLeft.equals("null")) {
                TreeNode leftChild = new TreeNode(Integer.valueOf(curLeft));
                cur.left = leftChild;
                dq.addLast(leftChild);
            }

            if (!curRight.equals("null")) {
                TreeNode rightChild = new TreeNode(Integer.valueOf(curRight));
                cur.right = rightChild;
                dq.addLast(rightChild);
            }

            left += 2; 
            right = left + 1;
        }
        return root;
    }
}

// Your Codec object will be instantiated and called as such:
// Codec ser = new Codec();
// Codec deser = new Codec();
// TreeNode ans = deser.deserialize(ser.serialize(root));

Graph

733. 图像渲染

经典的BFS和DFS

class Solution {
    boolean[][] visited;
    int[] dx = new int[]{0, 1, 0, -1};
    int[] dy = new int[]{1, 0, -1, 0};
    int[][] image;
    int n, m;
    public int[][] floodFill(int[][] image, int sr, int sc, int color) {
        n = image.length; 
        m = image[0].length;
        visited = new boolean[n][m];
        this.image = image;
        int originalColor = image[sr][sc];
        // dfs(sr, sc, color, originalColor);
        bfs(sr, sc, color, originalColor);
        return image;
    }

    private void dfs(int sr, int sc, int color, int originalColor) {
        if (sr < 0 || sr >= n || sc < 0 || sc >= m) {
            return;
        }

        if (image[sr][sc] != originalColor) return;

        if (visited[sr][sc]) return;
        image[sr][sc] = color;
        visited[sr][sc] = true;
        for (int i = 0; i < 4; i++) {
            dfs(sr + dx[i], sc + dy[i], color, originalColor);
        }
    }

    private void bfs(int sr, int sc, int color, int originalColor) {
        Deque<int[]> dq = new LinkedList<>();
        dq.addLast(new int[] {sr, sc});
        while (!dq.isEmpty()) {
            int size = dq.size();
            for (int i = 0; i < size; i++) {
                int[] cur = dq.pollFirst();
                int curX = cur[0], curY = cur[1];
                image[curX][curY] = color;
                visited[curX][curY] = true;
                for (int d = 0; d < 4; d++) {
                    int newX = curX + dx[d], newY = curY + dy[d];
                    if (newX < 0 || newX >= n || newY < 0 || newY >= m || image[newX][newY] != originalColor || visited[newX][newY]) continue;
                    dq.addLast(new int[] {newX, newY});
                }
            }
        }
    }
}

542. 01 矩阵

对于这种多源的问题我们可以反过来考虑，让终点入队，这里让终点入队的好处是我们就可以让每一个点都只被visited一次从而避免多次（至多4次）visit 节点

class Solution {
    int n, m;
    int[][] mat;
    int[] dx = new int[] {0, 1, 0, -1};
    int[] dy = new int[] {1, 0, -1, 0};
    public int[][] updateMatrix(int[][] mat) {
        // BFS 第一个碰见的一定是最近的
        this.n = mat.length; 
        this.m = mat[0].length;
        this.mat = mat;
        Deque<int[]> dq = new LinkedList<>();
        
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                if (mat[i][j] == 1) {
                    mat[i][j] = -1; // 这样既有visited过的效果又可以记录最短距离
                } else if (mat[i][j] == 0) {
                    dq.addLast(new int[] {i, j});
                }
            }
        }
        bfs(dq);
        return mat;
    }

    private void bfs(Deque<int[]> dq) {
        int level = 0;
        while (!dq.isEmpty()) {
            int size = dq.size();
            level++;
            while (size-- > 0) {
                int[] cur = dq.pollFirst();
                int curX = cur[0], curY = cur[1];
                for (int i = 0; i < 4; ++i) {
                    int newX = curX + dx[i], newY = curY + dy[i];
                    if (newX < 0 || newX >= n || newY < 0 || newY >= m || mat[newX][newY] != -1) continue;
                    mat[newX][newY] = level; // 相当于更新了visited 以及 答案
                    dq.addLast(new int[] {newX, newY});
                }
            }
        }
        return;
    }
}