收集些容易忽视的Java的用法

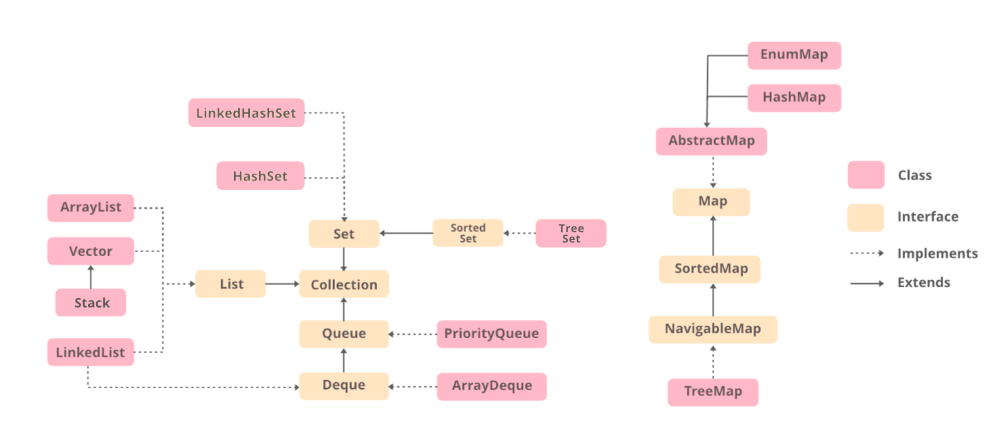
Java

Collections Interface

Collections Interface

List

ArrayList

LinkedList

LinkedList Methods:

Methods Description
addFirst() Adds an item to the beginning of the list.
addLast() Add an item to the end of the list
removeFirst() Remove an item from the beginning of the list.
removeLast() Remove an item from the end of the list
getFirst() Get the item at the beginning of the list
getLast() Get the item at the end of the list

Deque

LinkedList 实现

ArrayDeque 实现

总结

其实就是array和linkedlist区别，大部分时间里array会比较快。但是当添加元素时超了array的容积，则ArrayDeque需要resize.

Stream()

  1. List to array one line:
1
List.stream().mapToInt(i -> i).toArray();
  1. Print elements in an int[]:
1
Arrays.stream(ret).forEach(a -> System.out.print(a + " "));

Reduce()

有三个组成元素：

identity, accumulator, combiner:

  • Identity – an element that is the initial value of the reduction operation and the default result if the stream is empty
  • Accumulator – a function that takes two parameters: a partial result of the reduction operation and the next element of the stream
  • Combiner – a function used to combine the partial result of the reduction operation when the reduction is parallelized or when there’s a mismatch between the types of the accumulator arguments and the types of the accumulator implementation
1
2
3
List<Integer> numbers = Arrays.asList(1, 2, 3, 4, 5, 6);
int result = numbers.stream().reduce(0, (subtotal, element) -> subtotal + element);
assertThat(result).isEqualTo(21);

0 is identity

subtotal, element -> subtotal + element is accumulator

Pair

1
2
3
Pair<Integer, String> pair = new Pair<>(1, "One");
Integer key = pair.getKey();
String value = pair.getValue();

Comparator

在Arrays.sort中使用 Comparator:

1
2
3
4
5
6
Arrays.sort(costs, new Comparator<int[]>(){
    @Override
    public int compare(int[] o1, int[] o2) {
        return o1[0] - o1[1] - (o2[0] - o2[1]);
    }
});

在Collections.sort中使用：

1
2
3
4
5
6
7
8
9
Collections.sort(costs, new Comparator<List<Integer>>(){
    @Override
    public int compare(List<Integer> o1, List<Integer> o2) {
        int diff1 = o1.get(0) - o1.get(1);
        int diff2 = o2.get(0) - o2.get(1);
        return Integer.compare(diff1, diff2);
    }
});

和Map.Entry 结合在一起:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
List<Map.Entry<Character, int[]>> ls = new ArrayList<>(hm.entrySet());
Collections.sort(ls, new Comparator<Map.Entry<Character, int[]>>(){
    @Override
    public int compare(Map.Entry<Character, int[]> e1, Map.Entry<Character, int[]> e2) {
        Character e1Key = e1.getKey();
        Character e2Key = e2.getKey();
        int[] e1Value = e1.getValue();
        int[] e2Value = e2.getValue();
        int n = e1Value.length;
        for (int i = 0; i < n; i++) {
            int first = e1Value[i], second = e2Value[i];
            if (first == second) {
                continue;
            } else {
                return second - first;
            }
        }
        return e1Key - e2Key;
    }
});

通过位运算来互换大小写

大写字符与其对应的小写字符的 ASCII 的差为 32

也就是 1<<5

所以：

变换大小写这件事等价于：

  • 如果字符是小写字符，减去 32 得到大写字符；
  • 如果字符是大写字符，加上 32 得到小写字符。

而这两者合并起来，就是给这个字符做一次不进位的加法，即异或上 1 << 5。

为什么两者合并起来相当于一个不进位的加法?

考虑一下异或操作的特性：

  • 0 XOR 0 = 0
  • 1 XOR 0 = 1
  • 0 XOR 1 = 1
  • 1 XOR 1 = 0

这与不进位加法的规则相同，即：

  • 0 + 0 = 0
  • 1 + 0 = 1
  • 0 + 1 = 1
  • 1 + 1 = 0 (不考虑进位)

现在，考虑ASCII值。大写字母与其对应的小写字母的ASCII值之间的差异在第5位上。例如：

  • ‘A’ = 65 = 1000001 (二进制)
  • ‘a’ = 97 = 1100001 (二进制)

请注意第5位的差异。要从’A’转到’a’，我们需要将第5位从0变为1，这可以通过加32（即1左移5位）来实现。反之亦然。

当我们异或一个数字时，我们实际上是在为该数字的每一位执行不进位加法。因此，当我们对字符值进行异或操作1 << 5时，我们实际上是在进行以下操作：

  • 如果第5位是0（即该字符是大写字母），我们将其加上1，从而将该字符转换为小写字母。
  • 如果第5位是1（即该字符是小写字母），我们将其加上0，从而将该字符转换为大写字母。

因此，异或操作实际上是实现不进位加法的一种快速方法。在这种情况下，它可以用来在大写和小写字符之间进行快速切换。

代码：

1
cArr[startIdx] ^= 1 << 5;

使用此技巧的例题

784. 字母大小写全排列

这个题在 从二叉树到回溯到DP 中

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
    int n;
    List<String> paths = new ArrayList<>();
    char[] cArr;
    public List<String> letterCasePermutation(String s) {
        n = s.length();
        cArr = s.toCharArray();
        backtrack(0);
        return paths;
    }

    private void backtrack(int startIdx) {
        if (startIdx == n) {
            paths.add(new String(cArr));
            return;
        }
        if (Character.isDigit(cArr[startIdx])) {
            backtrack(startIdx + 1);
            return;
        }

        cArr[startIdx] ^= 1 << 5;
        backtrack(startIdx + 1);
        cArr[startIdx] ^= 1 << 5;

        backtrack(startIdx + 1);
        return;
    }
}

通过左括号指针判断括号是否合法：

思路是用代表左括号的指针移动，碰到左括号右移，右括号左移，如果left == 0证明合法，否则比如左括号的idx < 0则代表右括号>左括号数量，不合法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
private boolean isValid(String sb) {
    int left = 0;
    for (char c : sb.toCharArray()) {
        if (c == '(') {
            left++;
        } else if (c == ')') {
            left--;
            if (left < 0) {
                // 右括号比左括号多，肯定无效
                return false;
            }
        }
    }
    // 如果左括号的数量等于右括号的数量，才是一个有效的括号字符串
    return left == 0;
}

使用此技巧的例题

301. 删除无效的括号

在 从二叉树到回溯到DP

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
class Solution {
    StringBuilder sb = new StringBuilder();
    List<String> paths = new ArrayList<>();
    String s;
    int n;
    public List<String> removeInvalidParentheses(String s) {
        this.s = s;
        n = s.length();
        backtrack(0);
        return filterResult();
    }

    private List<String> filterResult() {
        // 筛选出最长的有效括号字符串
        int maxLen = 0;
        for (String str : paths) {
            maxLen = Math.max(maxLen, str.length());
        }
        HashSet<String> set = new HashSet<>();
        for (String str : paths) {
            if (str.length() == maxLen) {
                set.add(str);
            }
        }
        return new LinkedList<>(set);
    }

    private void backtrack(int idx) {
        if (idx == n) {
            if (isValid(sb.toString())) {
                paths.add(sb.toString());
            }
            return;
        }
        char c = s.charAt(idx);
        if (c != '(' && c != ')') {
            sb.append(c);
            backtrack(idx + 1);
            sb.deleteCharAt(sb.length() - 1);
        } else {
            // 选择当前的括号
            sb.append(c);
            backtrack(idx + 1);
            sb.deleteCharAt(sb.length() - 1);

            // 不选择当前的括号
            backtrack(idx + 1);
        }
        return;
    }

    private boolean isValid(String sb) {
        int left = 0;
        for (char c : sb.toCharArray()) {
            if (c == '(') {
                left++;
            } else if (c == ')') {
                left--;
                if (left < 0) {
                    // 右括号比左括号多，肯定无效
                    return false;
                }
            }
        }
        // 如果左括号的数量等于右括号的数量，才是一个有效的括号字符串
        return left == 0;
    }
}

StringBuilder

1
2
3
sb.append(c);
backtrack(idx + 1);
sb.deleteCharAt(sb.length() - 1);