目录

2834. 找出美丽数组的最小和 - 等差数列

204. 计数质数 - 埃氏筛

题解

2834. 找出美丽数组的最小和

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
    static final int MOD = (int)1e9 + 7;
    public int minimumPossibleSum(int n, int target) {
        int m = target / 2;
        if (n <= m) {
            return (int)(((long)1 + n) * n / 2 % MOD);
        } else {
            long firstPart = (((long)(1 + m) * m) / 2 % MOD);
            long secondPart = (((((long) target + target + (n - m) - 1) * (n - m)) / 2) % MOD);
            // System.out.println(firstPart + " " + secondPart);
            return (int)((long)(firstPart + secondPart) % MOD);
        }
    }
}

Quote: lc-2834

复习一下等差数列的求和公式：一个等差数列的和，等于其首项与末项的和，乘以项数除以2。所以从 1 一直加到 n 的和就是 (n + 1) * n / 2。

题目的基本思想是，如果 target = 7, n = 3，那么最优解就是取从 1 到 7 // 2 = 3：[1, 2, 3]，这样的和最小，所以就是取从 1 到 n 的 n 个数，和为 (n + 1) * n / 2。

但也有复杂情况，那就是如果 n > target // 2，例如 target = 7, n = 6，那么这时 [1, 2, 3] 后面如果继续添加元素 4，就会出现 3 + 4 = 7，违反了元素和不能等于 target 的要求，所以下一个元素只能从 target = 7 开始取，才能确保元素和不为 target。也就是需要在 target 起取 n - target//2 个数，最后的数组为 [1 .. target//2] + [target .. target//2 + n]，直接计算和即可。

204. 计数质数

埃氏筛（Sieve of Eratosthenes）的技巧在于标记数组中不是 Prime 的数。

思路大概是：

作者：Sweetiee 🍬
链接：https://leetcode.cn/problems/count-primes/solutions/507445/kuai-lai-miao-dong-shai-zhi-shu-by-sweetiee/
来源：力扣（LeetCode）

  1. 初始化长度 O(n) 的标记数组，表示这个数组是否为质数。数组初始化所有的数都是质数.
  2. 从 2 开始将当前数字的倍数全都标记为合数。标记到 sqrt(n) 时停止即可。具体可以看来自维基百科的动画：

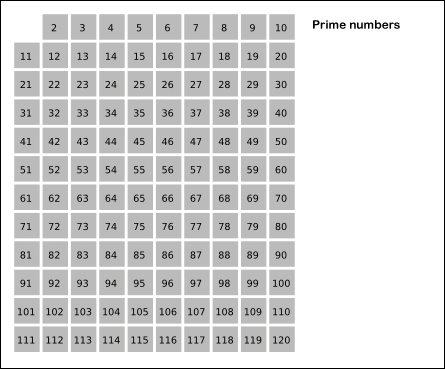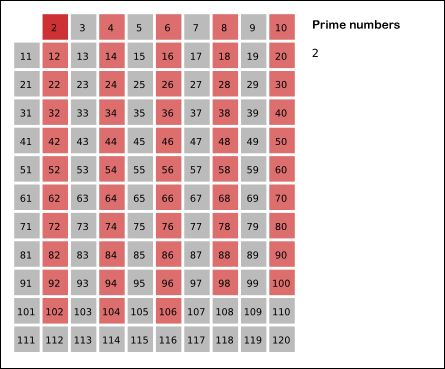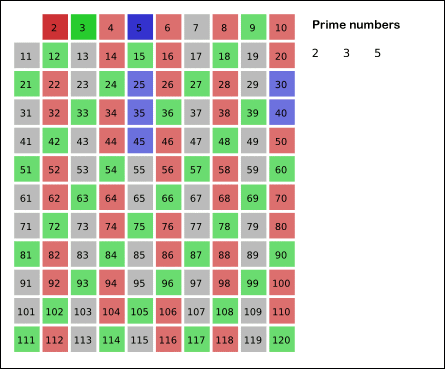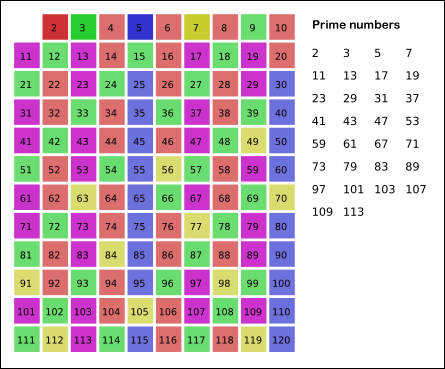
find_prime

这里有两个难点：

  1. 第一个是为什么 从 i 开始 到 sqrt(n) 结束
  2. 另一个是在标记Prime的时候为什么是从 i * i 开始

为什么 从 i 开始 到 sqrt(n) 结束

比如 n = 36

可以分为下面几对：

(1, 36)，(2, 18)， (3, 12)， (4, 9)， (6, 6)

在筛到 sqrt(36)时，

2 会去标记 4 6 8 … 36

3 会去标记 9 12 …

所有大于6的因数都会在小的因数标记时被标记因此不需要额外检查

为什么从 i * i 开始标记？

假设当前我们正在处理一个质数 x，那么它的倍数是 x,2x,3x,…

  • 这是因为，所有例如 2x, 3x, 在处理比 x 小的质数时已经被标记为合数了。
  • 举个例子，当你处理 2 的倍数时，已经标记了2, 4, 6, 8 当你处理 3 时，就不需要标记这些数了（比如6）

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public int countPrimes(int n) {
        // 埃氏筛
        boolean[] isPrime = new boolean[n];
        Arrays.fill(isPrime, true);
        for (int i = 2; i < Math.sqrt(n); i++) {
            if (isPrime[i]) {
                for (int j = i * i; j < n; j += i) {
                    isPrime[j] = false;
                }
            }
        }

        int cnt = 0;
        for (int i = 2; i < n; i++) {
            if (isPrime[i]) cnt++;
        }

        return cnt;
    }
}